蘇る天才アーベルのアイデア”その2”〜解の可換性と可解性と､その先に・・

　前回は､｢アーベルの証明｣(Pベシック著､山下純一訳)を参考にし､アーベルの代数方程式の非可解性の証明(不可能の証明)の概略について述べました。
　少し整理すると､アーベルは背理法を使い､方程式が代数的解を持つ形を特定し､5次方程式での矛盾を示す事で証明にこぎ着けた。
　そこで､一般の5次方程式をy⁵−ay⁴+by³−cy²+dy−e=0―①と書き､その解yをべき根と係数を含む形の代数式(有理式+無理式)で表し､更に､解yの代数式をy=p+ᵐ√R+p₂･ᵐ√R²+⋯+pₘ₋₁･ᵐ√Rᵐ⁻¹―②と表現。但し､mは素数､R,p,p₂,…はyと類似の代数式とし､元の方程式の係数の有理式(整式+分数式)になるまで続くとする。
　つまり､仮にyが5次方程式の解だとすれば､”yは係数とᵐ√Rの様な無理式を含む多項式の様な形で表現できる”とアーベルは考えた。こうした”代数学の原則”は既にオイラーが予想した一般形に近いが､アーベルは更にその先を行くものだ。

　証明の最初のSTEPだが､②式のp,p₂,p₃,…,pₘ₋₁,Rが方程式の解の有理式となる事を証明する。つまり､解は係数の無理式となるが､逆に､係数を解の代数式と見れば､簡単な多項式となる。但し､対称性で言えば､対称性を崩す事で√を使い､解を得る。
　次に､｢コーシーの置換論｣を使えば”5次方程式の解の有理式にて解を置換する時､5個又は2個の異なる値しか取らない”と言える。だがアーベルは､”5個の変数からなる有理式は､変数全体を置換する時にとる値が1〜5であれば､2個の異なる値をとる”と言い換えた。
　そこで､解の有理式ᵐ√Rにてm=5とすると､ᵐ√Rが解のあらゆる置換により5つの値をとる(つまりm=5となる)事の矛盾を導き､ᵐ√Rが解の置換により僅か2つの値(つまりm=2)をとる事を示した。
　つまり､代数的方法で解を求めようとする時､最初に開くべき根は平方根であるべきだが､もしそうだとすると､m=5と仮定すれば､⁵√Rの左辺が120個の値をとり､右辺は10個の値をとる様な等式が存在し､矛盾が導ける。
　故に､5次方程式をべき根で解く事は不可能だと結論できる。

　以上の様に､アーベルの戦略は非常に直線的だが､方程式がべき根で解けるならば､解が持つべき代数式を導き､この代数式を使って方程式の解を置換する時に矛盾が導ける事を示し､非可解性の証明とした。
　但し､この矛盾は5個の解を置換する時に､解がとる事のできる値の個数5に依存する。が､5以上の次数でも適用できる事は明らかである。

　そこで今日は､アーベルの代数的非可解性の3つ目の論文と､ガウスが提示した非可解性の例外の一般化について書きたいと思います。　

アーベルの模索〜可解性と可換性

　アーベルは､ヨーロッパ留学からの帰国後も非可解性の証明について考え続け､非可解性の持つ更に深い理由を模索していた。
　1828年3月､アーベルはクレレ紙に”方程式の代数的解法は一般的には不可能だが､ガウスが(アーベルよりも若い時に)発見した円周等分方程式:xⁿ−1=0では(既約であっても)常に代数的解法が可能である”と書いた。
　因みに､これはアーベルの非可解性に関する3つ目の論文であり､ガウスの逆鱗に触れた真の理由がここにあったのだ。
　アーベルは､この”ガウスの例外”を一般化しようと試みた。つまり､”この様な方程式は常により低い次元の方程式を使って解ける”との結論に達し､(ガウスが既に気付いてたであろう)”解の相互関係”を以下の様な簡単な形で与えた。

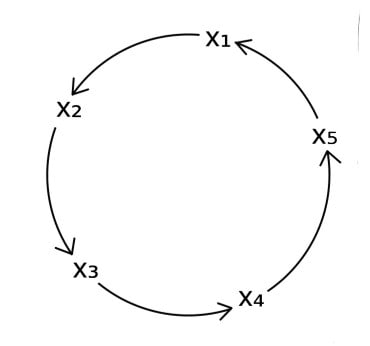
　まず､最初の解をx₁とし､次の解をx₂=f(x₁)と仮定し､fを2回適用したとして､f(f(x₁))=f²(x₁)と書く。この様に､解にfを順に適用すると､x₁,f(x₁),f²(x₁),…,fⁿ⁻¹(x₁)という解の列が与えられる。
　ここでnを方程式の次数とすると､n=5として､上の解の列が全て異なる解からなるとすれば､5次方程式は5個の異なる解しか持たないので､f⁵(x₁)=x₁となる。この時､5つの解x₁,x₂,x₃,x₄,x₅は円周上に巡回的に並べる事が出来る(上図参照)。
　因みに､方程式の解全体がこの様な”巡回的な対称性を持つ”時､その方程式は”巡回方程式”と呼ばれ､べき根で解ける。即ち､可解である。ここでアーベルは､円周等分方程式の可解性をヒントに､｢アーベル方程式｣の概念に到達する。

　これは､重根を持たないn次方程式の解をx₁,x₂,x₃,…,ₙとし､xの有理式により､xₖ=Φₖ(x₁)､k=2,3,…,nと書けるとし､更に､任意のi,jにて､Φⱼ(Φᵢ(x₁))=Φᵢ(Φⱼ(x₁))となる時､元の方程式を”アーベル方程式”と呼ぶ。
　アーベルはアーベル方程式が可解である事を証明したが､これは円周等分方程式で見れば､任意のjにて､Φⱼ(x₁)=Φ₁(xⱼ)=xʲ₁と書けるので､アーベル方程式の例となり､可解となる。また､アーベル方程式のガロア群はアーベル群(可換群)となり､逆にガロア群がアーベル群である様な既約方程式はアーベル群となる事も知られている。
　従って､”ガウスの例外”の一般化こそが､アーベル方程式を生んだとも言える。

　以上の様な､アーベルのアイデアと洞察により､可解性と可換性が結び付けられ､アーベルは数学史上初めて､可換性というものを考察の対象として取り上げた。
　こうしてアーベルは､アーベル方程式の解全体を巡回的なパターンの集まりに纏める事を可能にする。この様な場合は解の間の関係が可換な事は明らかで､これは2個の回転の結果はそれを行う順序によらないからだ。
　アーベルはこの”可換な解の対称性が重要だ”と主張した。だが､これだけでは方程式のパターンが巡回的かそうでないかを説明できない。事実､1828年の論文を”可換性についての疑問がどの様に発展したか？”という観点で見れば､更に驚くべきものとなる。
　しかし悲しいかな､この時点で命が尽きた。”まだやるべき事がゴマんとある”と言い残して・・・
　つまり､アーベルの不可能の証明には､続編があった。その続編を完璧にかつ簡潔に完成させたのが､もう1人の若き天才ガロアである。

　因みに､前回｢その1｣のコメントでも書いたが､”ガウスが非可解性を証明できなかったであろう”根拠として､ガウスは”解の相互関係”､つまり”解の(巡回的)対称性”までは気付いてたと思うが､コーシーの置換論にまで達してたかは疑問が残る。一方で､ガロアも置換論には精通してたし､その置換論が基盤となり､”方程式のガロア群”が生まれたとも言える。
　これは､アーベルがコーシーの置換論をヒントに代数的非可解性の証明を発見したのとよく似ている。勿論､ルフィニの”不完全な証明”がなかったら､コーシーの置換論もなかった訳ですが､今になってルフィニがアーベルと同等に評価されたのも頷けます。
　勿論､明確な根拠とは言えまいが､満更外れてはないと思う。

　
アーベルとガロア〜対称性と置換論

　この1828年は､アーベルとガロアが方程式の可解性に関する同じ問題を考えていた。
　アーベルが他界した年に､ガロアの父親は自殺するが､同じ年にガロアはガロア理論を発見する。
　一連のガロアの悲運の物語は､1826~27年のアーベルの失望を思い出させる。アーベルは自身が科学アカデミーに提出した｢パリの論文｣を紛失(或いは無視)したコーシーを”カトリックの頑固者”と批判し､1832年にそのスキャンダルが発覚すると獄中にいたガロアは”アーベルの死を疚しく感じる人物”と､コーシーに対し怒りを爆発させた。
　”哀れみはいらない。憎悪が全てだ”と言い放ち､一方的で不条理な決闘を受け､若干20歳の人生を閉じたガロアだが､彼の仕事はアーベルの結果と完全に一致する。

　こうしたガロアの新たな視点は､可解性の完全な理解へと結びつき､現代的手法での抽象化に向かう所にその本質がある。
　一方で､アーベルに欠けてたのはこの点で､アーベルの仕事を再定式化し拡張する事で､ガロアは1つ1つの方程式の解の置換を論じるより､多くの置換を一気に含む､より進んだ抽象化を経る方が好都合である事に気づいた。
　ガロアこそが､これらの置換を新しい種類の群という数学的対象として論じた最初の人物であり､これにより現代数学の全ての一般性とパワーを全開する方向に切り拓く。
　だが同時に､従来の理解の間に決定的なギャップも作り出した。つまり､現代数学が手にした新たなパワーは､高度な教育を受けた現代人をも無知なまま置き去りにし､そのまま放置されたのだ。
　こうしたギャップはどうすれば埋める事が出来るのか？
　とりわけ､”対称性と置換”というアーベルとガロアに共通した議論を､我々は扱う必要がある。

　一方で､”方程式が代数的に解けるという事は､ある種の可換な対称性に対応(依存)する”という観点に到達できる。
　これは､2次方程式の解の公式でも明らかだが､αとβを入れ替えてもα+βとαβの値は変わらない。つまり､前回で触れた様に､解と係数の関係で表される基本対称式は可換(=アーベル的)と言える。
　以上から､対称性のある所には何らかの不変量があり､その”対称性さえ崩せば､べき根で解を求める事が出来る”との重要な事実が隠されている。

　でも､”対称性を崩す”とはどういう事なのか？
　例えば､ラグランジュがやった様に､2次方程式x²+bx+c=0の解α,βのルート部に注目すると､b²−4c=(α−β)²となり､解α,βの入れ換え(置換)で変化しない事が判る。また､√(b²−4c)=√((α−β)²)=α−βとすれば､αとβの置換で､α−β→β−α=−(α−β)と変化するので､解の置換に対し対称ではない。
　従って､係数の四則で得られた対称式(=b²−4c)の√を取る事で解の値は､±の非対称性を生み出す。故に､ルート内の数の対称性(不変性)を崩し､2次方程式の解の公式を可能にする。
　つまり､方程式の解を得るには”対称性のある”係数を組み合わせ､”対称性のない”解を作る必要がある。が､四則だけでは対称性を崩せず､故に､2次以上の方程式では四則に加え､√演算を加え､解α,βをべき根で得る事を可能にする。

　3次方程式にても同様で､x³+bx²+cx+d=0の解をα,β,γとすると､b=−(α+β+γ)､c=αβ+βγ+γα､d=−αβγより､係数b,c,dは解α,β,γの置換について対称である。
　そこで､α=A+³√(B+√C)+³√(B−√C)､β=A+³√(B+√C)ω+³√(B−√C)ω²､γ=A+³√(B+√C)ω²+³√(B−√C)ωとする。但し､ωは1の3乗根とし､A,B,Cは有理式とする。
　C=−((α−β)(β−γ)(γ−α)/6)²/3となり､上と同様に､√内の(α−β)²(β−γ)²(γ−α)²は解α,β,γの置換(入替え)について不変(対称)だが､√を取ると√((α-β)²(β-γ)²(γ-α)²)=±(α-β)(β-γ)(γ-α)は偶置換だけが不変である。
　因みに､”偶置換”とは､互換を偶数回して得られる置換の事で､偶置換の場合､解α,β,γの差積(α-β)(β-γ)(γ-α)は不変であり､奇置換では−1倍となる。
　故に､Cでは√を取っただけでは完全に対称性が崩せない。そこで､³√(B±√C)を調べる。
　B+√C=((α+ω²β+ωγ)/3)³,B−√C=((α+ωβ+ω²γ)/3)³で､³√(B+√C)³=(α+ω²β+ωγ)/3,³√(B−√C)=(α+ωβ+ω²γ)/3となり､(α+ω²β+ωγ)³は偶置換だけで不変だが､α+ω²β+ωγは恒等置換を除く全ての置換で対称性が崩れる。以上より､³√(B±√C)の対称性は完全に崩れるので､解α,β,γは√と四則で得る事が可能となる。

　この様に､√や³√を使う事で段階的に対称性を崩し､4次方程式の場合は(ずっとややこしくなるが)同様の手順で､まず平方根を取り､次に立方根を取り､という手順で1つ1つ対称性を崩し､√と四則を使って解く事を可能にする。即ち､対称性を下げていく過程を段階的に追う事で非可解性を示す。
　つまり､5次以上の方程式が一般的には”代数的に解けない”事を一言で言えば､5次以上の方程式は”√を取る事では崩せない対称性を持つ”と言え､故に､”べき根では解の公式を作れない”となる。
　
　
補足〜ガウスによる解の置換の対称性

　因みに､ラグランジュは3次や4次方程式にても､カルダノやフェラーリの解法において3乗根や平方根により解の置換の対称性が崩れていく様を丹念に観察した。が､5次方程式を前にして頓挫してしまう。
　一方でガウスは､円周等分方程式:xⁿ−1=0がべき根によって解ける事を示したが､その学位取得論文(ルフィニと同じ1799年)の中で”5次以上の方程式は一般にはべき根で解けないだろう”と書いている。
　因みに､この3年前にガウスは､正17角形の作図可能性を証明したが､x¹⁷−1=(x−1)(x¹⁶+･･･+x+1)=0の解を複素平面上にプロットできれば作図可能となる。故に､この16次方程式を対称性の視点から眺め､4つの2次方程式に分け､√と四則のみで解いてしまう。
　つまり､定規とコンパスでの作図可能性を証明した事で､ラグランジュの対称性の理論を整数論に応用し､幾何の難問を解いてみせたのだ。

　確かに､この理論のポイントは”解の置換”にあるが､5次以上の方程式でもべき根で解けるケースがある。
　x⁵−1を例に取ると､x⁵−1=(x−1)(x⁴+x³+x²+x+1)より､x⁴+･･+x+1=0の解を求めればいい。
　そこで､x=1以外の全ての解を(x₁,x₂,x₃,x₄)とすれば､1の4乗根σ(σ⁴=1)={−1+√5+√(10+2√5i)}/4となるから､(x₁,x₂,x₃,x₄)=(σ,σ²,σ³,σ⁴)と置ける。ここで､解x₁=σの置き換え先が決まれば､他のx₂,x₃,x₄の置き換え(4通り)も自動的に決まり､代数的な解の公式で解く事が出来る。
　つまり､x⁴+x³+x²+x+1=0は一般の4次方程式とは対称性が明らかに異なる。事実､3次方程式の解:5/16,(−5+2√5)/16,(−5−2√5)/16を含み､実質は2次方程式になる。
　更に､n≥5のxⁿ−1=0にても同様で､一般のn次方程式とは対称性(可能な解の置き換え)が異なり､その対称性の性質に基づき､解をべき根で求める事が可能にはなる。

　事実､”ガウスの円周等分方程式論がなかったら､アーベルの定理もガロア理論もありえなかったろう”と､｢私のガウス｣の高瀬正人氏は語っている。
　確かに､そうかも知れない。
　事実､アーベルは上でも述べた様に､円周等分方程式論を一般化し､アーベル方程式を発見した。更に､”解の対称性”ではなく”可換な解の対称性”に着目し､可換性と可解性を結びつけた。ガロアですら気付かなかった可換性の先をアーベルは見つめていた。
　つまり､代数的非可解性には続編があったのだ。その続編を殆ど同時期に受け継いだのが､もう1人の若き天才ガロアである。

　故に､円周等分方程式論だけでは､代数的非可解性の明確な証明に辿り着けるとは思えない。が､ガウスの”例外”の発見がヒントになったのも事実ではある。