もう10年以上も前?・・・熱流体解析を行う際に最初に購入したのがこの本。
『数値流体工学 / 荒川 忠一・著 / 東京大学出版会』 しかし、当時の私にとっては非常に難しく、一つ一つのプロセスに対して、その計算が何をやりたいのか?と言う全体的な意図がなかなか見えなかった・・・と言うのが正直な感想です。この本で初めて「SIMPLE解法」と言う手法の存在を知りましたが、肝心の「SIMPLE解法」以前にスタッガード格子系やコントロール・ボリューム法の段階で既に、かなりの消化不良の状態に陥っておりました(爆)。
そんな中、薦められるままに購入したのが、この本。
『流れの数値計算と可視化 / 平野 博之・著 / 丸善』 この時、既に基礎方程式の導出過程については相当理解が進んでいたので、後半の「数値計算法」を集中して読みました。この本では「MAC法」の系列をベースとした解法を取り扱っており、MAC法の進め方が自分にもしっくりと来るものでした。この本で学んだMAC法が現在の数値モデルのベースになっています。この本は、私にとって数値流体解析のバイブルと言っても過言ではないでしょう。
そして現在読んでいるのが、この本。
『流れの数値計算と可視化 第3版 SIMPLE法とMAC法による熱流体解析 / 平野 博之・著 / 丸善』 私にとってのバイブルとなった本の著者が、あの「SIMPLE解法」について解説する、という事で購入しましたが、必要最小限の記述に留めるとの事で、式の詳しい導出過程は余り無く・・・と思いきや、ここであの『数値流体工学』と合わせて読むと、パズルのピースを合わせて行くかの如く、SIMPLE解法の全体像が漸く見えてきました。それにしても数式の導出過程が複雑で、この計算は一体何をしているの?とその導出過程の意図を見失いかけた事も度々・・・(どこが「シンプル」なんだ!)。
久々に、初心に帰って2次元キャビティ流れの計算プログラムを書いてみました。使用したのは勿論、SIMPLE解法です。基礎方程式の離散化にはハイブリッド法、時間発展は1次精度オイラー前進差分を使用しました。MAC法はエクスプリシットなのに対して、SIMPLE解法はセミ・インプリシットなので時間刻みの条件がMAC法程厳しくないのがメリットです。
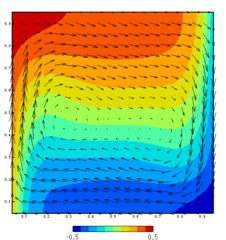
基礎方程式を多重積分して離散方程式を導き、それらをアルゴリズムの形に整理した上で、プログラムを構築して実行する、と言う一連のプロセスを行った事で、漸く全体像が掴めてきました。今度は3次元化とより高精度なスキームの適用を目指して行きたいですね。
『数値流体工学 / 荒川 忠一・著 / 東京大学出版会』 しかし、当時の私にとっては非常に難しく、一つ一つのプロセスに対して、その計算が何をやりたいのか?と言う全体的な意図がなかなか見えなかった・・・と言うのが正直な感想です。この本で初めて「SIMPLE解法」と言う手法の存在を知りましたが、肝心の「SIMPLE解法」以前にスタッガード格子系やコントロール・ボリューム法の段階で既に、かなりの消化不良の状態に陥っておりました(爆)。
そんな中、薦められるままに購入したのが、この本。
『流れの数値計算と可視化 / 平野 博之・著 / 丸善』 この時、既に基礎方程式の導出過程については相当理解が進んでいたので、後半の「数値計算法」を集中して読みました。この本では「MAC法」の系列をベースとした解法を取り扱っており、MAC法の進め方が自分にもしっくりと来るものでした。この本で学んだMAC法が現在の数値モデルのベースになっています。この本は、私にとって数値流体解析のバイブルと言っても過言ではないでしょう。
そして現在読んでいるのが、この本。
『流れの数値計算と可視化 第3版 SIMPLE法とMAC法による熱流体解析 / 平野 博之・著 / 丸善』 私にとってのバイブルとなった本の著者が、あの「SIMPLE解法」について解説する、という事で購入しましたが、必要最小限の記述に留めるとの事で、式の詳しい導出過程は余り無く・・・と思いきや、ここであの『数値流体工学』と合わせて読むと、パズルのピースを合わせて行くかの如く、SIMPLE解法の全体像が漸く見えてきました。それにしても数式の導出過程が複雑で、この計算は一体何をしているの?とその導出過程の意図を見失いかけた事も度々・・・(どこが「シンプル」なんだ!)。
久々に、初心に帰って2次元キャビティ流れの計算プログラムを書いてみました。使用したのは勿論、SIMPLE解法です。基礎方程式の離散化にはハイブリッド法、時間発展は1次精度オイラー前進差分を使用しました。MAC法はエクスプリシットなのに対して、SIMPLE解法はセミ・インプリシットなので時間刻みの条件がMAC法程厳しくないのがメリットです。

基礎方程式を多重積分して離散方程式を導き、それらをアルゴリズムの形に整理した上で、プログラムを構築して実行する、と言う一連のプロセスを行った事で、漸く全体像が掴めてきました。今度は3次元化とより高精度なスキームの適用を目指して行きたいですね。


















最近CFDについて勉強し始めている者です!
SIMPLE法についてなのですが
収束判定はどのようにしていますでしょうか?
運動量の残差がある一定以下になったら収束というようにしているのでしょうか?
お返事いただければ幸いです。
宜しくお願い致します。
Navier-Stokes方程式から圧力に関する方程式を導出して、これをどのように解くかが「核」となります。その後、得られた圧力条件を満たすように速度成分を求めて行きます。
この際の圧力を得るための解法(圧力解法)は主に、陽的(explicit)に解く方法と半陰的(semi-implicit)に解く方法があります。前者はMAC法やfractional-Step法で、後者はSIMPLE法が挙げられます。
ちなみに、私はSIMPLE法ではなく、MAC法をベースとした手法を用いています。
MAC法をベースにされているのに申し訳ありません。
SIMPLE法のフローを簡単に書きますと
以下のようになりますが、④の部分が「鍵」となり、
そこでの残差が一定以下になったら良いということでしょうか?
③、④を解く際にも収束条件が必要になると思うのですが、それとはまた別に考えるということになるのでしょうか?
分かりにくくてすみませんが宜しくお願い申し上げます。
①START
↓
②速度,圧力の初期値設定
↓
③離散化した運動量保存式を解く
↓
④圧力の補正式を解く
↓
⑤圧力及び速度を補正
↓
⑥収束判定
【1.圧力と運動量の各々で収束判定】
①START
↓
②速度,圧力の初期値設定(初期条件)
↓
③離散化した運動量保存式を解く
↓
④圧力の補正式を解く
↓
⑤収束判定(圧力&運動量)(収束→⑥、未収束→③)
↓
⑥圧力及び速度を補正(境界条件)
【2.圧力のみで収束判定(MACはこのフロー)】
①START
↓
②速度,圧力の初期値設定(初期条件)
↓
③圧力の補正式を解く
↓
④収束判定(収束→⑤、未収束→③)
↓
⑤離散化した運動量保存式を解く(既に圧力が判っている)
↓
⑥圧力及び速度を補正(境界条件)
私はMAC系を中心に用いているので、先に圧力を決めてから、速度(運動量)を決める方法を採用しています。SIMPLE法を用いた場合も、圧力のみの収束判定を用いました。
ただ、この辺は技術者の考え方にもよるので一概に言えません。
記事で紹介した著者の場合、フローチャートを見ると、荒川先生は「圧力と運動量」、平野先生は「圧力のみ」のようです。
二つの違いは記事で紹介されている著書を参考にさせて頂きたいと思います。
以下の場合の③、④において
それぞれTDMAやヤコビ法などを用いて反復計算すると思うのですが、
③、④における反復計算の収束判定と
⑤での収束判定は別のものとして考えたらいいのでしょうか?
それとも下のように考えるものなのでしょうか?
一般的なフローによく書かれている最後の収束判定と各反復計算での収束判定の違いがよく分からないです。
【1.圧力と運動量の各々で収束判定】
①START
↓
②速度,圧力の初期値設定(初期条件)
↓
③離散化した運動量保存式を解く
↓
③'収束判定(運動量)(収束→④、未収束→②)
↓
④圧力の補正式を解く
↓
④'収束判定(圧力)(収束→④、未収束→②)
↓
⑤全体として収束判定(圧力&運動量)(収束→⑥、未収束→②)
↓
⑥圧力及び速度を補正(境界条件)
①START
↓
②速度,圧力の初期値設定(初期条件)
↓
③離散化した運動量保存式を解く
↓
③'収束判定(運動量)(収束→④、未収束→②)
↓
④圧力の補正式を解く
↓
⑤収束判定(圧力)(収束→⑥、未収束→②)
↓
⑥圧力及び速度を補正(境界条件)
何回も申し訳ございませんが、宜しくお願い致します。
> ⑤での収束判定は別のものとして考えたらいいのでしょうか?
これもやり方は色々とあります。
確かに
「Uの残差だけで収束判定」
「Vの残差だけで収束判定」
「Pの残差だけで収束判定」
とやる方法もあると思います。
また、
「U、V,Pの残差をひっくるめて収束判定」
と扱う方法もあります。
U,V,Pなどのパラメータは「無次元化」することで数値の大きさ(オーダー/スケール)を揃えることができます。
従って、U,V,Pなどをひっくるめて、その中で「最も大きな残差」が一定の値(閾値)より小さくなれば、収束したと判定する方法もあります。
現在はサンプルプログラムが掲載されている専門書も多く出版されています。色々なプログラムのやり方を見て研究されるのが宜しいかと思います。
その中で、自分が理解しやすいと思えるようなプログラムが見つかれば、それをベースに自分なりに工夫して、アレンジして行くことで理解が深まります。
本当に有難うございます。
何度も何度も申し訳ございませんでした。
今までは理論のところばかり見ていましたが
これからはサンプルプログラムも見て研究していきます。
また質問させていただくこともあるかもしれませんが
宜しいでしょうか...?
引き続き、研究頑張って下さい。
フローチャートでは一つの記号で表記される内容でも、
プログラムで記述すると何行にも渡る処理も多々あります。
その一つ一つの計算は、実際に試行錯誤を重ねて行くなかで、自ずと理解が深まるものと思います(経験上)。
わからない自分が嫌になったりしますが
あきらめずに頑張ってみようと思います。
重ね重ね本当に有難うございました。