いま、回転軸の周りを半径r[m]、角速度ω[rad/s]で円運動する質量m[kg]の質点を考えます。この時、質点mの速度v[m/s]はv=rωで表されます。
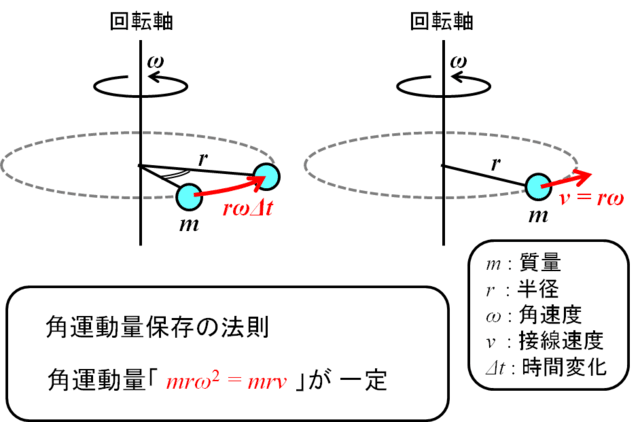
ここで運動量は「(質量)×(速度)=mv=mrω」で定義されます。また、運動量が保存される「運動量保存の法則」も高校の物理でお馴染みと思います。主に直進運動を考える場合です。
回転運動の場合は新たに、角運動量「(質量)×(半径)×(速度)=mrv=mrω2」という物理量を考えます。この角運動量が保存される「(角運動量)=(質量)×(半径)×(速度)=(一定)」というのが「角運動量保存の法則」です。
この考え方を空気塊の回転に応用してみましょう。ここでは、円筒形の空気塊が回転している状況を考えます。
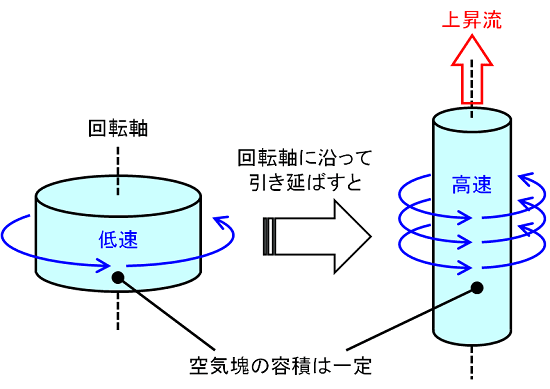
まず、左側の状態では回転半径が大きく、ゆっくりと回転しています。この空気塊が、何らかの理由で生じた上昇流によって、鉛直方向に引き延ばられる状況を考えてみます。
すると、右側のように細長くなってしまいます。つまり、容積は一定のまま、回転半径は小さくなります。先の「角運動量保存の法則」の考え方に基づけば、半径が小さくなる分、回転速度が増すことになります。
(※厳密には、空気塊の状態までを考慮した「渦位」という物理量があります。この「渦位」については、気が向いたらまたの機会に・・・)
このメカニズムが働く現象にはどのようなものがあるのか、2つの例を紹介します。
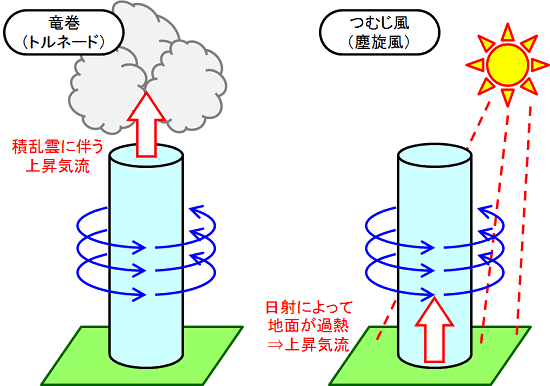
竜巻は「積乱雲に伴う活発な上昇流」によって発生するものです。この上昇流によって、空気塊は鉛直方向に引き延ばされることで、強い渦が形成されます。
一方、つむじ風(塵旋風)は「地面が日射によって加熱されることで生じる上昇流」によって発生します。この上昇流によって、空気塊は鉛直方向に引き延ばされます。
両者は一見すると形が似ていますが、上昇流の要因は異なります。

ここで運動量は「(質量)×(速度)=mv=mrω」で定義されます。また、運動量が保存される「運動量保存の法則」も高校の物理でお馴染みと思います。主に直進運動を考える場合です。
回転運動の場合は新たに、角運動量「(質量)×(半径)×(速度)=mrv=mrω2」という物理量を考えます。この角運動量が保存される「(角運動量)=(質量)×(半径)×(速度)=(一定)」というのが「角運動量保存の法則」です。
この考え方を空気塊の回転に応用してみましょう。ここでは、円筒形の空気塊が回転している状況を考えます。

まず、左側の状態では回転半径が大きく、ゆっくりと回転しています。この空気塊が、何らかの理由で生じた上昇流によって、鉛直方向に引き延ばられる状況を考えてみます。
すると、右側のように細長くなってしまいます。つまり、容積は一定のまま、回転半径は小さくなります。先の「角運動量保存の法則」の考え方に基づけば、半径が小さくなる分、回転速度が増すことになります。
(※厳密には、空気塊の状態までを考慮した「渦位」という物理量があります。この「渦位」については、気が向いたらまたの機会に・・・)
このメカニズムが働く現象にはどのようなものがあるのか、2つの例を紹介します。

竜巻は「積乱雲に伴う活発な上昇流」によって発生するものです。この上昇流によって、空気塊は鉛直方向に引き延ばされることで、強い渦が形成されます。
一方、つむじ風(塵旋風)は「地面が日射によって加熱されることで生じる上昇流」によって発生します。この上昇流によって、空気塊は鉛直方向に引き延ばされます。
両者は一見すると形が似ていますが、上昇流の要因は異なります。

















