西願寺 岩倉

写真は、観音堂（左）と本堂（右）

西願寺は、元は今の三条大橋東詰のバスターミナルにあった浄土宗寺院です。
四軒寺の1つと云われていましたが、1979年に岩倉の地に移転しています。

アクセス
白川通を北上します。修学院、宝ヶ池や花園橋も越えます。
やがて八幡前駅周辺で叡電の踏切を渡ります。
公共交通機関の場合はこちらが最寄りですが、ここから徒歩で1.5kmあります。
さらに直進して約800m先で本道は左にカーブしますが、真っ直ぐに側道を進みます。ひたすら道なりに進むと、途中で石の一ノ鳥居をくぐります。
やがて左手に長谷土田公園が見えてきます。
この公園の右手の側道に入ると、突き当り右手に坂があります。
この坂を登ると、西願寺の駐車場があります。

駐車場の奥に観音堂が、左手に本堂があります。
お厨子は通常閉まっており左右には不動明王像と毘沙門天像がお祀りされています。

観音堂の後に進むと左手に本堂、左手奥に庫裏、正面奥には表門があります。
通常本堂は閉まっています。
表門の向こうには石段があり、本来はこの下から入ってきます。

朝日観音御開帳
毎年8/1の7:30頃から午前中は、観音堂が開扉されます。
観音堂の蔀戸とお厨子が開かれ、菅原道真公の念持仏と云われている聖観音菩薩像に直接お参りできます。
また当日は本堂も開放されています。
本堂の内陣中央には本尊の阿弥陀如来像と観音勢至菩薩像が左右にお祀りされています。
右脇壇には観音菩薩像、善導大師像、法然上人像が、左脇壇には地蔵菩薩像などがお祀りされていました。
御朱印や由緒書きはないとのことでした。

洛北マイナー散策の索引

「京都のおすすめ」の総合索引へ

長男くんの塾の問題6（算数 ただの図形の問題！？）

久々に長男くんの塾の算数の問題です。
今回、問題自体はそれほど難しくないです。
長男もやり方は分かっていました。
が、計算を間違えて不正解。

今回のポイントは、
これは確かに図形の問題ですが、
試験問題の中の1問とみた場合、
何の問題か、
ということでしょう。

興味のある方は、1度やてみて下さい。
本当に今回は、決して難問ではないです。


解答



上図のように、左の正方形は1辺12㎝、中央の正方形は15㎝、右の正方形は9㎝です。
なので、全体の面積は、
12×12＋15×15＋9×9＝144＋225＋81＝450。
この半分は225。
ウの下の欠けた部分は12×3＝36。

アイから下の長方形の面積は、225＋36＝261。
アイの長さは12+15+9＝36。
よってタテの1辺は、241÷36＝29/4。

最後に3cmを引くと、アウは29/4－3＝17/4

長男くんの解答用紙を見ても、そうやって解こうとしてます。
しかし残念ながら、計算を途中で間違えていました。
「惜しかったね。次は計算を間違えないようにしよう」で片づけるのは、普通の受験生。

さて今回はここからです。
受験の場合、「問題が解ければいい」だけではないでしょう。
算数も複数出題されるので、容易な問題は「早く正確に」解けると有利というか、志望校によってはそうしないと勝ち残れません。
そうした場合、有効なのが「先に答えまでの立式だけをして、計算は後でまとめてしてしまう」戦法です。

そうすることで、
・立式→計算→立式→計算と頭を切り替える必要がないので、劇的に勘違いや頭を切り替えるロスタイムが減る
・まとめて計算した方が、計算量も減る
のです。

具体的には、下のようになります。



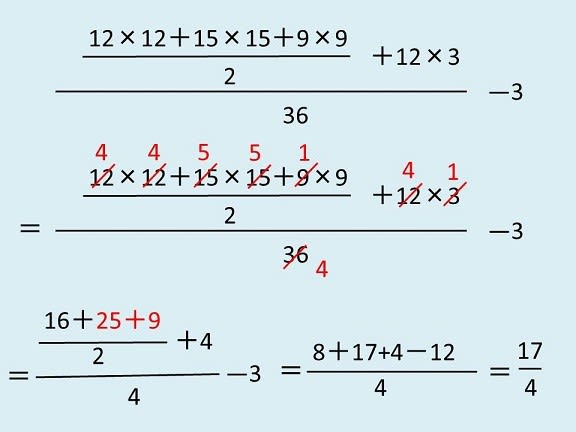
1列目が取りあえず答えまで立式だけしたものです。
あとは問題用紙をかなぐり捨てて、計算だけします（笑）。

その際に左手の大きな分数は、2列目のように各項9で割れ、36が約分出来ます。
すると3列目の左まで、式が簡単になります。
さらに赤い奇数同士を足してから2で割り、－3を分子に乗せると、中央のようになります。
よって17/4。

ご覧のように、この方法だと、
劇的に計算量や頭の切り替えが減るので、
計算間違いも減り、解答時間も短くなるんです。
まあこういうのが正に「受験テクニック」になるんでしょうね。
僕も「大学受験の時」は可能な限りこの方法で数学、物理、化学は解いていました。

しかし「小学生で」ここまでケア出来るのが、灘のレベルなんでしょうね（笑）。

「京都のおすすめ」の総合索引へ