ケーキをコンパスと定規だけで7分割しよう〜正17角形の作図”その５”

　このクソ暑い中で､3話続けての数学ネタですが､どうかお付き合いくださいませ。
　前回｢その4｣では､ガウスの正17角形の作図可能性を少し突っ込んで説明しましたが､今回は､そのガウスですら解けなかった正7角計の作図について書きたいと思います。

ケーキを7等分するには

　数学を愛する会(@mathlava)さんが開催した､”ケーキを7等分する”選手権。
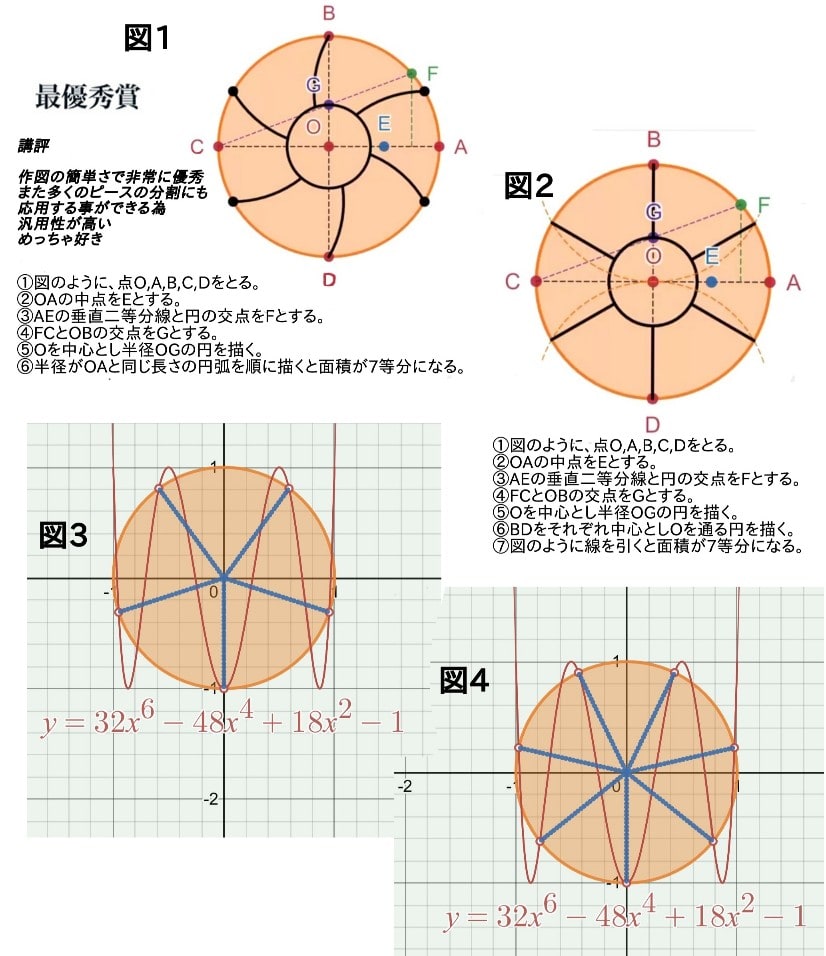
　最優秀賞に輝いたのは､｢定規とコンパスでケーキを7等分するの図｣と題して投稿されたカット方法(図1)。”作図の簡単さで非常に優秀”と大絶賛の講評を獲得した。
　確かに､きれいな作品ではある。円周を7等分するではなく､コンパスで丸いケーキの内側に小さな円を描き､更にケーキ全体を6等分する事で､(小円も含め)結果的に7分割する。デザインもシンプルで､審査員受けしそうだだ。
　がしかし､既にこれと殆ど同じ7分割は､(曖昧な理由で)没となってたが登場しており(図2)､私には少し不公平に映った。それに､6等分する部分が抜け､説明不足にも思えた。

　それに､7等分と同じ面積に7分割するの区別がよくわからない。
　ただ､図1の7分割の証明は図形の相似条件(面積比は辺の比の2乗)を使えば､中学生でも出来る？とあるが､相似という点で言えば､図2の方がずっとわかりやすい。
　更に､屁理屈に聞こえるかもだが､ロールケーキなら簡単に7等分出来るし､形が全く同じ7等分であるので､一応は数学的でもある。　
　一方で､ケーキを7等分する一般的なやり方で一番ポピュラーなのが､アルミホイルで横長の長方形を作り､それをタテに8等分し､正8角形の枠を作る。更に､8番目の区画が重なる様にテープで止めれば､正7角形の枠を作れる。
　が､これは厳密には正7角形ではない。つまり､円周を7等分する様な”正7角形はコンパスと定規だけでは作図出来ない”事が知られてるからだ。わかり易く言えば､円周の360度を7で割ると51.4285714285と･･･続く無限小数になり､(分度器を使っても)正確に七角形を表現できない。

コンピュータと数学の違い

　因みに､コンピュータ･プログラミングを使えば(内角が無理数であろうが)あらゆる正n角形が正確に描ける。例えば､正三角形なら定規とコンパスで簡単に作図できるが､コンピュータだと､その内角120度=2π/3=2.09439510239･･･というラジアンの単位を使って計算する。
　つまり､コンパスと定規だけで作図出来る正n角形も､コンピュータでは無理数という奇妙数を使った計算の繰り返しで､数学的な美しさを持つとは言い難い。が､出来上がった三角形はとても美しい。
　”数学とコンピュータは同じじゃないの”って疑問に思う人も多いだろうが､数学は毅然とした明確かつ合理的な論理の学問であり､コンピュータは無理数などの曖昧な数字を扱う道具に過ぎない。言わば､数学的幾何学的美しさの対極にある。
　しかし､今私達が目にする殆ど全ての図形は､コンパスと定規ではなく､コンピュータで(数学から見れば)いい加減に計算されたものだ。というのも､一般的なコンピュータが扱えるのは数学的精密さを持つ数式の処理ではなく､浮動小数点数という(数学的に見れば)デタラメな計算の道具である。
　故に､”コンピュータでは正7角形を簡単に瞬時に描けるのに､なぜ分度器では描けないのだろうか”と疑問の思うかもしれないが､”正7角形が定規とコンパスでは描けない”とした方が数学的にも辻褄が合うし､都合がいい。故に､数学のルールでは”正7角形は描けない”となる。
　しかしそんな数学は完全じゃないから､コンピュータで補完する必要がある。
　これを厳密に説明すれば､コンピュータでは三角関数をテイラー展開で求めるが､テイラー展開で三角関数を求めるにはオイラーの公式が前提となる。この公式はラジアン(360°=2π)が必須だから､コンピュータでは三角形を描くのにラジアンという無理数を扱う。
　以上より､コンピュータが数学を補完するカラクリが理解出来たでしょうか。　
　

不可能を可能にしたチェビシェフの多項式

　話は大きく横道に逸れましたが・・・
　では､天才ガウスでさえ解けなかった正7角形は､どうやって作図できるのか？
　実は､(定規とコンパスではなく)チェビシェフ多項式だけを使って円周をn等分する方法があるらしい。
　実際､座標平面にy=32x⁶-48x⁴+18x²-1のグラフを描くと､単位円の円周との交点が正7角形の頂点になってるのだ。更に､同じ式で正5角形も作れるという(図3と図4)。
　つまり､円と多項式の交点で円周をn等分する問題に帰着する訳だが､チェビシェフ多項式を使えば簡単に作成できる。
　まず､(第一種)チェビシェフ多項式だが､以下のような漸化式で表される。
T₀(x)=1
T₁(x)=x
T₂(x)=2x²−1
T₃(x)=4x³−3x
T₄(x)=8x⁴−8x²+1
・・・
Tₙ₊₁(x)=2xTₙ(x)−Tₙ₋₁(x)､n:自然数

　実はこの多項式は､Tₙ(x)=cos(nt)と見る事で､cosの倍角公式そのものになっていて､以下の様に表す事が出来る。
cos(0)=1
cos(1t)=x=cos(t)
cos(2t)=2(cos(t))²−1
T₃(x)=4(cos(t))³−3(cos(t))
T₄(x)=8(cos(t))⁴−8(cos(t))²+1
・・・
　つまり､チェビシェフ多項式を使えば､円周をn等分及びn+1等分する多項式を作る事が出来るのだ。
　以下､｢チェビシェフ多項式を使って円周を等分する方法｣を参考にまとめます。
　そこで､y=Tₙ(x)とx²+y²=1の交点を求めてみます。
　まず､x²+y²=1上の点を(x,y)=(cos⁡(θ),sin⁡(θ))と媒介変数表示する(0≤θ<2θ)。これをy=Tₙ(x)に代入すれば､sin⁡(θ)=Tₙ(cosθ)=(cos⁡(nθ))=sin(π/2−nθ)となり､sin⁡(θ)−sin(π/2−nθ)=0を得る。
　更に､和→積の公式で変形すれば､sin⁡(θ)−sin(π/2−nθ)=2cos⁡(π/4−(n−1)θ/2)sin⁡(−π/4+(n+1)θ/2)=0となり､cos⁡(π/4−(n−1)θ/2)=0又は､sin⁡(−π/4+(n+1)θ/2)=0を得る。
　つまり､θ=3π/2(n−1),7π/2(n−1),11π/2(n−1),⋯,(4n−5)π/2(n−1)､又は､θ=π/2(n+1),5π/2(n+1),9π/2(n+1),13π/2(n+1),⋯,(4n+1)π/2(n+1)となる。
　これは､θが円周(2π)ををn−1等分またはn+1等分する事が確認できる。
　例えば､n=6とすれば､T₆(x)=y=32x⁶-48x⁴+18x²-1とx²+y²=1との交点は､θ=3π/10,7π/10,11π/10(=π/10),
5π/10,9π/10､または､θ=π/14,5π/14,9π/14,13π/14,17π/14(=3π/14),7π/14,11π/14､となり､円周を5等分または7等分する交点になってる事が判る。
　少し､急いで説明しましたが､グラフに書いて1つ1つ確認すれば､理解しやすいです。

追記

　古代ギリシャ時代から考えられてきた､定規とコンパスという幾何学的な方法で等分するではなく､n次多項式を使ってn等分する所に数学の美しさとロマンが凝縮されてるようにも思う私である。
　正n角形を作図する事は(数学的に言えばだが)､xy座標上の円周をn個の円弧に分割する事と同じで､更に､複素平面上の単位円をn個の円弧に分割する事は､1のn乗根を求めるのと同じでした。
　故に､(代数学の)拡大体の理論で言えば､正n角形が作図できる条件は､xⁿ−1の最小分解体Eが作図可能体になる事です。
　つまり､[E:Q]=Φ(n)=2ᵏとなる。
　以下､作図可能な正多角形(物理のカギしっぽ)を参考にまとめます。

　前回の｢その4｣でも述べましたが､これは､作図可能体Eが有理数体Qの拡大体である時､拡大次数は2も累乗になり､[E:Q]=2ʳで表し､[E:Q]=Φ(n)が2の累乗のものに限る事から判る。
　逆に､Φ(n)=2ᵏの場合､ガロア群g(E/Q)=(Zₙ)ˣの位数は2ᵏとなり､正規部分群の組成列として{e}=G₀⊂G₁⊂･･･⊂Gₖ=g(E/Q)が得られる。更に各部分群にて､|Gᵢ|=2ⁱとなり､かつ可解群となる。これに対応してEの部分体の昇鎖列(Q=E₀⊂E₁⊂･･･⊂Eₖ=E)を考える事が出来る。
 　また､隣り合う部分体はガロア拡大になっていて､ガロア理論の基本定理により拡大次数にて､|Eᵢ:Eᵢ₋₁|=|Gₖ₊₁₋ᵢ:Gₖ₋ᵢ|が成り立つ。これより､[E:Q]は2の累乗になる(証明終)。

　そこで､正n角形が作図可能とすると､オイラー関数Φ(n)を考える事になり､Φ(n)=2ᵏ書ける。因みに､オイラーのΦ関数とは､nと互いに素なn以下の自然数の個数Φ(n)を与える数値関数である。
　一方で､コンパスと定規だけで線分を2等分する事は簡単にできるので､ある1つの正多角形が描ければ､その倍の正多角形を描く事も簡単です。故に､必然的に奇数角の正多角形に興味が向く。しかし､(素数以外の)因数を持つ奇数については､例えば3×7=21角形の様に､正7角形が描けないのに正21角形が描ける筈もない。逆も真なりで､正21角形が描ければ正7角形も描ける。
　結局､素数角の正多角形の作図可能性を調べるのが本質的に重要となる。

　そこで､pを素数とすると､2~p−1の数は全てpと互いに素より､Φ(p)=p−1。一方で､正n角形が作図可能な為には､Φ(p)=2ᵐと書けるので､p=2ᵐ+1を満たす。
　つまり､素数角形で作図可能なのは､p=2ᵐ+1と表わせる素数に限る。
　では､p=2ᵐ+1の形の素数はどんな数があるのか？
　仮に､奇数vを用いてm=uvと書けるとすると､2ᵐ+1=(2ᵘ+1)(2ᵘ⁽ᵛ⁻¹⁾−2ᵘ⁽ᵛ⁻²⁾+･･･−2ᵛ+1)と因数分解できるので､これはp=2ᵐ+1が素数である事に反するので､mはどんな奇数でも割れない数となる。故に､m=2^qとなる。
　以上より､正p角形が作図可能可能となるのは､p=2^(2^q)+1の場合に限られる。
　また､この形の数をフェルマー数と呼び､個の数が素数の時をフェルマー素数と呼ぶ。
　フェルマー素数は､オイラーの発見やガウスの考察などにより､現在では3,5,17,257,65537の5つしか存在しない事が知られている。故に正p角形が作図可能なのは､p=3,5,17,257,65537の5つの時だけとなる。

　以上､後半は前回｢その4｣とダブる所も多かったんですが､正17角形の作図可能性については(出し尽くした感もあり)､これで終りにしたいと思います。
　計5回に渡り､長々と説明してきましたが､正17角形の作図可能性という幾何学の領域を代数的可解性という代数学の領域に推し進め､更には”体の拡大論”という現代の代数論として大きな華を咲かせたガウスのアイデアは､見事という他ありません。
　まさに､現代に甦るガウスのアイデアをこの5話の中に詰め込んだつもりですが､ガウスに関しては｢超天才ガウス｣(1話~5話)でも続ける予定なので､こちらの方も宜しかったら眺めて下さい。
　では・・・