解の対称性から見たガロア理論〜ガロアをめぐる旅”その１８”

　過去､計17話にてガロアの定理を説明してきましたが､十分に説明するのはやはり困難が付き纏いますね。
　というのも､アーベルが”代数的に解けない”と主張した5次以上の既約方程式でも､(以下でも述べるが)ガウスが証明した様に､円周等分方程式なら､べき根で解ける。
　しかしその例外を､(方程式の解を置換して得られる)ガロア群の可解性を使って証明したのが､若き天才ガロアでした。
　因みに､ガロアの定理は”代数方程式の解が四則演算と冪根だけで表わせる必要十分条件はガロア群が可解である”というものでしたが､いつの間にか”5次方程式は代数的に(べき根では)解けない”という単純な方程式論になります。
　巷で説かれてるガロア理論の多くは､アーベルの代数的可解性の証明をガロア群(置換論)を使って説明したに過ぎず､実際にガロア理論の本質を把握するのは､少し混乱が伴います。
　事実､前回｢その17｣のガロア定理の証明も､単純な既約方程式を基本的なガロア理論で説明しただけでした。
　

解の対称性とガロア群

　そこで今日は､5次方程式の代数的可解性を解の対称性を使って説明したいと思います。
　まず､ガロアの理論の中核は､集合という概念がなかった時代に”群”と呼ぶ画期的な手法である置換論を導入し､方程式の持つ解の対称性(解の置換)に注目する事で､無数にある方程式のパターンを”有限集合の数え上げ”に落とし込んだ事にある。
　勿論､5次方程式を解く研究の流れを大きく変えたのはラグランジュ(仏)ですが､4次方程式までは､16世紀の天才数学者のカルダノ(伊)やフェラーリ(伊)の発見により､係数から方程式の解の公式を何とか求める事が出来た。だがラグランジュは方程式の解で係数や補助方程式の解を表そうとした。
　つまり､ラグランジュの”分解式”である。

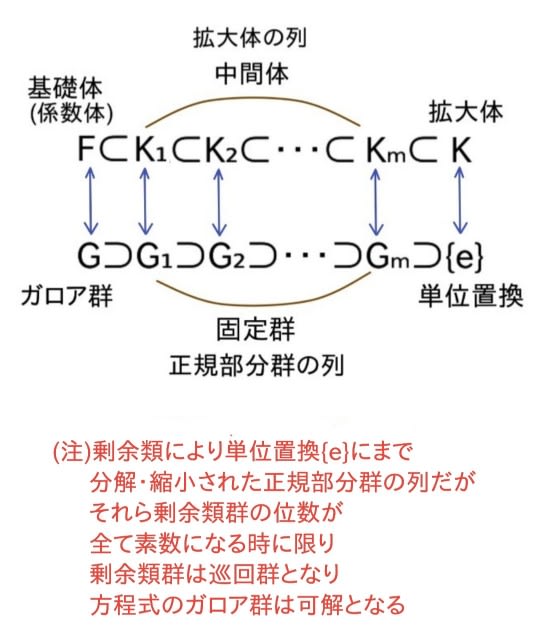
　仮に､ガロア群Gに正規部分群Hが存在するなら､Gを剰余類分解すればHに､HはH₁に､H₁はH₂に縮小し､G⊃H⊃H₁⊃H₂⊃…{e}との列を作る。この時､H₁,H₂,…も正規部分群になり､剰余類は群をなす。それぞれの剰余類群が素位数pであれば､(この時に限り)剰余類群は巡回群(可換群)となり､可換性を保持した部分群の列が存在し､方程式はべき根で解ける。
　つまり､”ガロア群に単位(恒等)置換{e}に至る正規部分群の列が存在し､それら剰余類群の位数が全て素数となる”事が､方程式が代数的に可解である為の必要十分条件となる。が､前回｢その17｣で証明した様に､剰余類が巡回群となる様な部分群の系列は存在しなかった。

　わかり易く言えば､ガロア群Gを正規部分群Hにより分解すると､G=H+αH+…という等式を得て､この時､剰余類:H,αH,…のなす群を剰余類群と呼ぶ。この剰余類群の位数が素数ならば､ガロア群は可解となる。
　これは､位数を素数pとする剰余類群は(1,2,…,p)を生成元とする巡回群となるので､正規部分群の置換では変化しない。
　そこで､その他の置換で変化する根の有理式Vの多項式をgとし､それぞれの剰余類の置換でθがθ,θ₁,θ₂,…と変化したとすれば､θ,θ₁,θ₂,…によるラグランジュの分解式Eは､1のp乗根をζとして､E=θ+ζθ₁+ζ²θ₂+…と書ける。更に剰余類群は巡回群で巡回置換により､EはζᵏEと変化するので､剰余類群の置換でEᵖは変化しない。
　故に､位数を素数pとする剰余類群の時に限り､Eᵖは基礎体に含まれ､そのp乗根を求める事でEが求まるというカラクリである。
　つまり､方程式の係数体(基礎体)Fに分解式Eを添加すれば､体はガロア拡大体にまで拡大し､それに対応するガロア群Gはその最小の正規部分群{e}(=恒等写像)へと(分解され)縮小する。こうした正規部分群の列を満たすガロア群を可解群と呼ぶ。

　因みに”剰余類群”とは､素数pの倍数を除く整数全体の集合をGとすると､pで割った余りが1である集合をHとする時､G(の元)は掛け算で群を成し､剰余類:H,2H,…,(p-1)Hにより､G=H+2H+…+(p-1)Hと分解される。この剰余類が群である事は明らかで､p=7の時は､3H×4H=12H=5Hとなり､掛け算で閉じている。この時､右剰余(3H)=左剰余(H3)となるので､(定義より)HはGの正規部分群となる。
　つまり､正規部分群であれば(右剰余=左剰余となり)剰余類は壊れず､剰余類全体が剰余類群となる。
　ガロアが苦労して発見したのが､この正規部分群である。即ち､解の置換で得られたガロア群Gに(剰余類分解で作った)正規部分群の列(G⊃H⊃H₁⊃H₂⊃…⊃{e})が存在し､その剰余類群が全て素位数pとなれば剰余類群は巡回群となる。故に､それらに対応する方程式はXᵖ=Aの形をしており､べき根(p乗根)で解ける事になる。

　因みに､｢天才数学者はこう解いた｣(木村俊一著)では､5次方程式を解く為に､ガロア群を正12面体の60通りの(対称軸)回転操作に置き換え､その中から素位数の巡回群を割り出し､正規部分群を見出すが､結局はそんな部分群は見つからないから､べき根で解けない事を証明した。が詳しくは､後日述べる事にする。

ラグランジュの分解とガウスの発見

　一方でラグランジュは､”解の有理式”の存在を発見し､幾つも存在する3次や4次方程式の公式の謎を解いてみせたのだ。つまり､解の有理式から議論を始めれば5次方程式の謎も解ける筈で､解が有理式こそが代数的可解性に繋がると踏んだ。
　当時の天才数学者たちは､解の有理式が無限に存在する事に気づいていた。が､その全てを調べる事なんて不可能である。そして､同じ様にラグランジュも大きな壁に跳ね返された。
　そこで､5次方程式が代数的に解けない事を主張していたルフィニは､方程式の解の置き換えに群というツールを見出し､置換群に目をつけた。この群についてはラグランジュやコーシーも研究はしていた。だが､彼らも群の先にある正規部分群には気付いてはいなかった。

　この様に､ガロア以前に方程式論に画期的な業績を遺したのはラグランジュである。
　事実､ガロア群の”基礎体”(係数体)や”単拡大”定理は全て彼が確立したものだ。お陰で､ガロア理論はラグランジュ理論の完成形だとみなされる事も多い。
　以下でも述べるが､ラグランジュは”解の対称性”を破壊して解の公式が作れる事を発見した。つまり､√を使う事で対称性が壊れるのだ。事実､3次や4次方程式の解法にても､3乗根や平方根により対称性が壊されるが､5次方程式ではべき根では壊れない。

　このラグランジュによる解の対称性と方程式の関係を､劇的に展開させたのがガウスである。ガウスは円周等分方程式((xⁿ−1)/(x−1)=xⁿ⁻¹+…+1=0)がべき根で解ける事を証明したが､これはラグランジュの解の対称性(分解式)を利用したものだ。
　事実､(x¹⁷−1)/(x−1)=x¹⁶+…+1=0の16次の既約方程式は4つの2次方程式に分解され､2次方程式なら(結果として)”正17角計がコンパスと定規で作図できる”事の世紀の大発見に繋がった。
　事実､この方程式のガロア群の位数が10で､位数2,2,2,2の剰余類群､つまり素位数の巡回群に分解できるから､2次のラグランジュ分解が使える。故に､(方程式の)ガロア群は可解群となり､例外的にだが､べき根で解ける。
　冒頭でも述べた様に､ガロアの定理を”ガロア群の可解性”という必要十分条件で見れば例外なく正しいが､単に”べき根で解ける”との視点では例外が生じる。言い換えれば､”方程式がべき根で解ける”と”ガロア群が可解群である”とは､理解において雲泥の差がある。
　つまり､ガロアの定理の本質が”ガロア群の可解性にある”と考えた方が混乱は少ない。

　当然ガロアは､ガウスの整数論を熟知していた。遺書となった第一論文の中にもガウスの手法は幾度も現れる。
　｢その17｣のコメントにある様に､ポアソンは､”方程式が既約かどうかをまずは確かめる必要がある”とガロアの定理を棄却した。
　そこでガロアは､体の拡大により､既約が可約に変わる例として､(xⁿ−1)/(x−1)=xⁿ⁻¹+…+1=0を挙げた。一方でガウスが証明したのは､既約方程式のxⁿ⁻¹+…+1=0がべき根で解ける事でした。
　事実､その論文の中で､方程式の解く難しさは､それに添加される根により異り､1つの根の添加により既約方程式を可約に出来るとガロアは説いた。これは､xⁿ⁻¹+…+1=0にx=1という根を添加する事で､(xⁿ−1)=(x−1)(xⁿ⁻¹+…+1)=0と､既約方程式を可約に出来る事を示している。

　ここに､ガロア拡大体の理念が隠されてる訳だが､(四則演算で閉じる)体の中でべき根を求める演算では体を飛び出す。故にガロアは､べき根を方程式の係数体に添加した拡大体を考えた。つまり､べき根を加えて係数体を拡大すると既約方程式も可約となるケースが存在する。言い換えると､拡大体の構造を調べれば､べき根で解けるか否かが判別できる。
　一方､ガウスの｢代数学の定理｣では､複素係数の全ての方程式は複素数体上で可約になる(複素数の範囲内では必ず解が存在する)。が､べき根を有限回添加し拡大するだけでは複素数体には到達できない。
　そこでガロアは､べき根だけで方程式が解けるには､係数体にべき根を添加し､体の拡大を通して方程式の解の構造を調べた。つまり､べき根を加えた拡大体の系列の構造をガロア群に対応させる事で代数的可解性に着目した。だが､上述した様に”既約が可約に変わる”という例外が生じてしまう。
　因みに､(複素数の範囲でなら)方程式に”解が必ず存在する”と予想したのはオイラーが最初でした。後に､カントールとデデキントにより実数が確立され､ガウスの｢代数学の定理｣が正しい事が証明された。

アーベルとルフィニ､そしてガロアへ

　因みに､ガロアの第一論文のタイトルは｢べき根で方程式が解ける条件について｣だが､ガロアの遺書通り､ガウスやヤコビら当時の著名な数学者に送られた筈だが､これといった反応はなかった。彼らがガロア理論を理解できなかった筈はない。だが､”時間がない”と慌てて書き上げた論文は､簡潔すぎて議論を追うだけでも苦労する。
　ガウスは､5次以上の既約方程式が(円等分方程式の例外を除き)一般にはべき根では解けない事を見抜いていた。
　アーベルとルフィニは､係数体にべき根を含めた拡大体を調べる事で､代数的可解性の有無を判別できる所までは辿り着いていた。
　他方でガロアは､方程式の解の置換を群として捉え､その要素を取り出し､部分群の系列を調べた。つまり､部分群が簡単な構造の系列(正規部分群)であれば､べき根で解ける事を発見したのだ。
　但し､”この証明を完璧にする為に必要なものがあるが､僕には時間がない”と走り書きし､ようやく正規部分群の発見がある。つまり､ガロア理論の中核である正規部分群の生みの苦悩が､この遺書には十全に詰まっている。

　注目すべきは､ガロアは”方程式が代数的可解である必十条件としてガロア群が可解となる”としたが､アーベル=ルフィニの定理では”一般の5次の代数方程式がべき根により可解にならない”との事でした。事実､アーベルはx⁵―ax⁴+bx³―cx²+dx―e=0(a,b,c,d,e,fは有理数)を一般の5次方程式とし､これが代数的に可解でない事を証明した。
　この2つの定理をよく眺めると､後者は前者の十分条件を成してるのが判る。
　両者とも､方程式の”解の対称性”を起点とし､係数体にべき根を含めた拡大体を考察するが､ルフィニはべき根拡大列に全ての零点(解)が含まれる事で可解性を示した。更にアーベルは､べき根拡大列の最小分解体が”これ以上分解できない”事を証明し､可解性を説いた。つまり､最小分解体をべき根拡大体が含めば､方程式はべき根で解ける。
　一方でガロアは､拡大体と部分群を(逆向きに)1体1で対応させれば､べき根拡大列の最小分解体がガロア拡大体となり､恒等写像{e}に対応し､ガロア群の部分群が正規部分群になる事に着目した。

　つまり､方程式のガロア群がそれら正規部分群の列を含み､素位数の巡回群(=可換群)を満たす時に限り､解がべき根のみで得られ､可解群となる事を証明した。
　｢その17｣で書いた様に､一般の5次方程式の解から作った体の自己同型の群は5次の対称群と同型になり､5本のアミダくじの様に120個もの元をもつ。この群は十分に複雑な構造であるが故に､可換性を保持した”簡単な”正規部分群のガロア系列は存在しない。故に､この方程式はべき根では解けないとなる。

最後に〜ガロア理論と置換論

　これを”解の対称性”で言えば､対称性を崩す(つまり√を取る)事で､方程式の係数のみで作った係数体(基礎体)を拡大し､全てのべき根が入る様なガロア拡大体を作る事ができ､べき根だけの解の公式が得られる。
　これは､解の対称性があれば基礎体の元が､対称性が崩せれば拡大体の元が判定でき､べき根を含めた拡大体が作れる。つまり√を取る事で(対称性を崩し)､代数的に解ける様になるからだ。

　解がべき根で解けるには､元の基礎体からべき根を加えて拡大し､全ての根が入る様に拡大体を作れればいい。
　つまり､方程式のガロア群が巡回群になれば､元の基礎体からべき根を付けて拡大できる。更に拡大し､拡大体の列の全てが巡回群(つまり可換群)であれば､最小分解体がガロア拡大となり､体の拡大列に含まれる。
　この時､ガロア群の部分群は正規部分群の列を作り､その最小の正規部分群である恒等写像{e}に行き着く。この時に限り､方程式はべき根で解ける。つまり､ガロア群は可解群となる。

　ガロア理論により､解の置換がなすガロア群の部分群が(中間体という)拡大体の列に(逆向きにだが)1対1に対応できる(イラスト参照)。
　故に､解の対称性を考察する事で､体の拡大が元の基礎体(有理数体)から作れるかを判別でき､代数的可解性を特定できる。
　ガロア理論の本質は､数という無限の世界を扱う時､このガロア理論により拡大体の列を解の置換､つまり群論と対応させる事で有限の世界を調べる事を可能にする所にある。
　つまり､ガロア理論という置換論は､方程式論の為だけにあるのではないとも言える(｢解の公式が作れる事｣より)。

　以上､｢ガロアの論文を読んでみた｣(金重明著)も一部参考にしてまとめました。
　次回は､解の対称性とガロア群について､少し踏み込んで紹介したいと思います。