先日書いた「前半」と「中盤」と「IUT理論」で、「ABC予想」とその帰結の「IUT理論」の概要は掴めたかと思いますが。どうも話が抽象的過ぎて、上手く伝わりませんね。
そこで今日は、ABC予想の証明についてです。前半と同じく”異世界から来た論文を巡って”から一部抜粋です。
2016/7/6の記事ですが、結構突っ込んで紹介してあるので、参考にはなると思います。
これも長くなりますが、ご勘弁をです。
前人未到の数学的概念に挑め!
「ABC予想」は、1980年代にフランスの数学者リュシアン•スピロが提唱した「スピロ予想」と本質的にはほぼ同じものだ。
ABC予想は整数の関係に内在する数学的現象を説明し、一方でスピロ予想はその楕円曲線内の関係を説明するものだ。因みに、スピロ予想では、楕円曲線が特定の代数方程式がもつ全ての解の集合に幾何学的体系を与えている。
フェルマーの定理の様に、整数を楕円曲線として捉えなおす事は、数学の世界ではよく行われる。これにより予想の証明はより抽象的かつ複雑になるが、同時に数学者はその問題に関してより多くの手法を用いる事ができる様になる。
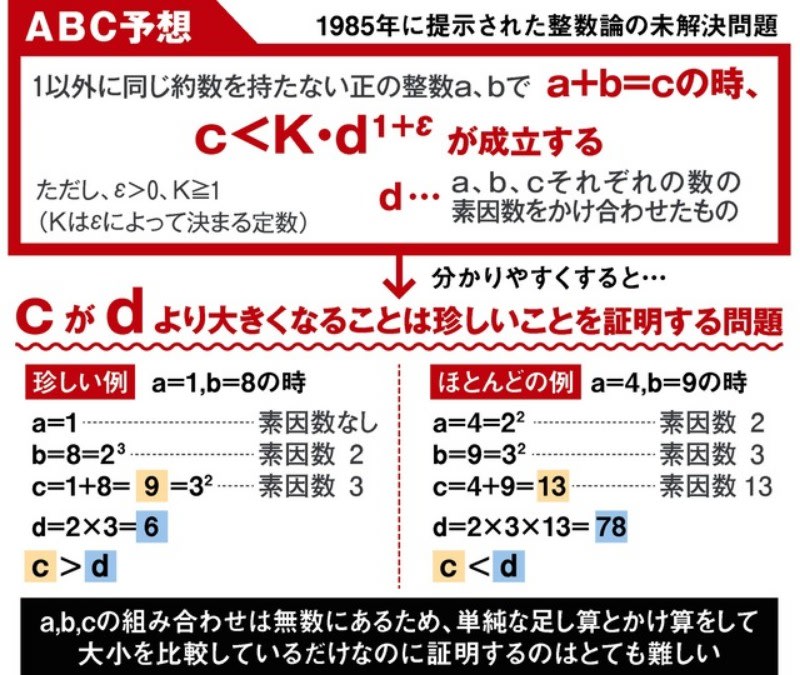
判り易く言えば、整数や素数の問題は多項式に置き換えた方が証明の見通しが良くなるという事です。
これは、ガウスやアーベルやヤコビが追いかけ、リーマンやワイヤシュトラウスが確立した楕円関数論とそっくりな展開ですね。
アンドリュー•ワイルズが1994年に、「フェルマーの最終定理」を証明した時、彼はまさにこの戦略を取った。
”2より大きい整数nに関し、等式「aⁿ+bⁿ=cⁿ」を成立させる正の整数の解はない”という問題をただシンプルな等式のまま扱うではなく、2度の変換を通し、より抽象的な定式化を行ったのだ。1度目は楕円曲線で、2度目が楕円曲線の「ガロア表現」と呼ばれる(群の行列表現を使った)別の数学的手法である。こうして、彼はフェルマーの定理の証明に成功した。
因みに、ペレルマンの「ポアンカレ予想」の証明(2003)の時も彼は、ウィリアム•サーストンの幾何化予想を解決し、その”系”としてポアンカレ予想を解決しますが。その時に採用した手法がリチャード•ハミルトンの発見したリッチフロー(ハミルトン=ペレルマンのリッチフロー理論)と統計力学を用いた独創的なものであった。
望月氏も同様の戦略を採った。ABC予想を直接証明するではなく、スピロ予想の証明にまず着手した。
その証明を行う為にまず、スピロ予想の関連のある全ての情報を”フロベニオイド”と呼ぶ自らが生み出した、新たなレヴェルの数学的概念へ変換します。
前述の”IUT理論”に関する研究を始める前、望月氏はABC予想の証明を目指し模索しながら、新しい変換に取り組んだ。
彼はこの一連の概念を「楕円曲線のホッジ•アラケロフ理論」と呼んだ。しかし残念ながら、これはABC予想に適用できない事が判明したが、彼はその過程でこの”フロベニオイド”という概念を生み出したのだ。
望月教授の”フロベニオイド”理論とは?
この”フロベニオイド”を理解する為に、頂点がA,B,C,Dの順に並んだ正方形を考える(右下を頂点A、右上を頂点B)。
この正方形はその物理的な位置はそのままの状態で、様々に動かす事ができる。例えば、反時計回りに90度回転したり(頂点が右下からD,A,B,Cと)。180度、270度または360度と回転させたり、ひっくり返して対角を入れ替えたりもできる。
こうして物理的な位置が保持される幾何的性質は、正方形の”対称性”と呼ばれ、故に、全ての正方形はこの様な対称性を8つ(4×2)有する。
更に様々な対称性を追求しようと、数学者は正方形全ての頂点にラベル(A,B,C,D)を与え、それらを集合と捉え、更にその集合に代数構造を付加した。
つまり、ABC予想という数論を、まず”フロベニオイド”幾何学上で考え、集合論(群論)に置き換え、代数学と融合させたんです。
この代数構造が付加された集合は、”群”と呼ばれ、群が正方形という幾何学的制約から自由になると、新たな”対称性”が得られる。
つまり、幾何学上の正方形においてはAが常にBの隣にある為、幾何学的制約をもつ剛体運動によっては、(A,C,B,D)という順番の頂点をもつ正方形はできない。しかし、その群の中のラべルだけで考えると全部で、順列組合せの24通り(=4×3×2×1)のパターンが存在しうる。
この様に、ラべルの対称性がもつ代数的集合は、その幾何学的制約を取り払う事で3倍(8→24)の情報を持つ。正方形より複雑な対象であれば、数学者はそれらの追加された対称性から、オリジナルの図形を用いるだけでは到達できない知見を得る事ができる。
望月教授が生み出した”フロベニオイド”は、先ほどの”群”の概念とよく似てる。ただそれは正方形ではなく、特殊な楕円曲線から抽出された代数的集合だ。
上記の例と同様に、フロベニオイドは元の幾何学的性質より生じる対称性よりも多くの対称性を有した。ここで望月氏は、楕円曲線に関するスピロ予想から得られるデータの多くをフロベニオイドに転換した。
ワイルズがフェルマーの最終定理から楕円曲線へ、さらにガロア表現へ手法を展開したのと全く同じ様に、望月氏は「ABC予想」から「スピロ予想」へ、更に”フロベニオイド”へ問題を展開させる事で情報量を増やし、証明を試みたのである。
”望月教授によると、それは”数”という世界の背後にある、より根本的な事実を模索する事です”とキムは言う。つまり、抽象的概念が追加されてく事で、これまで明らかでなかった関係性が表出するというのだ。
”抽象的なレヴェルにては、幾何学的なレヴェルよりも多くの事物の関係性が存在しているのです”
困惑と希望の間で
カンファレンス3日目の最後の発表と4日目の冒頭で、カリフォルニア大の数論学者キラン•ケドラヤが、ABC予想の証明にて望月氏がフロベニオイドをどの様に用いようとしてるかを説明した。
彼のレクチャーにより、望月教授の手法にて何が中核を成してるかが明らかにされ、それまでの時点で最も意義深い進展となった。
一方、望月教授の博士論文の指導教官であったファルティングスは、ケドラヤの講演が”インスパイア(啓発)されるべきものだった”とメールに記した。
”ケドラヤの講演は、そのカンファレンスにおける重要なポイントでした”と出席したスタンフォード大の数論学者のブライアン•コンラッドは語る。”その日は沢山の人に連絡しました。こんなテーマがケドラヤの講演で話されたから、明日とても興味深い事になるだろうってね”
しかし結局は、そううまくは事は運ばなかった。
望月教授の”フロベニオイド”という概念により説明されたABC予想は、驚くべきと同時に好奇心をかき立てられる発明だった。だが、それによって最終的な証明がどうなるのかまで説明されてる訳ではない。
しかし、カンファレンスに集まった数学者たちは、このケドラヤによるフロベニオイド概念の講演により、望月氏の手法がスピロ予想の定式化にどの様に繋がるのか?初めてその真意を理解した。
ただ次のステップこそが重要である。この証明を説明する為に、フロベニオイドによる転換が如何に”新しくかつ有効な手法”なのかを示さなくてはならないのだ。
この手法は望月教授が発表した先の”4つの論文”に記され、それがカンファレンスのラスト2日間の議題となった。
この論文の説明を担当したのは、パデュー大学のチャン•パン•モクと、京大数理解析研究所の星裕一郎と山下剛だ。3人は、IUT理論の理解に集中的に取り組む数少ない数学者である。しかし、誰も彼らの話にはついていく事ができなかった。
テキサス大学の数論学者フェリペ• ヴォロックは同カンファレンスに出席し、ブレイクスルーを期待してたが、そうはならなかった。
”参加者すべてが戸惑ってました。誰も手がかりを掴めてませんでした”と、コンラッドはその心情を語った。
”講演という短い時間に提供された情報量があまりに多過ぎて、専門用語の嵐だった為に皆途方に暮れてました”
僅かな前進、そして大きな一歩
フロベニオイドがIUT理論でいかに用いられるかを説明する最後の講演が失敗に終わった事は予測できたと考える参加者は多い。
”最後まで理解できるという僅かな望みもあった。ただ、あの部分は原論がより難解になっている。だから、私の後に担当した発表者に責任がある訳ではない”とケドラヤは語る。
最後の講演が失敗に終わった背景の一部には、”文化の違い”もあった、とキムは考える。説明を担当した山下と星は2人とも日本人だ。”日本では、数学者がプレゼンを行う場合、用語の定義を絶えず続ける傾向にある。文化的違いが現れたのです”とキムは言う。
”忍耐力と集中力が必要とされる内容が濃く詰まったスライドが日本では受け入れられるのですが。アメリカの場合は弁証的で双方向なスタイルが好まれる”
このカンファレンスを通じ、一部の人が実際に期待してた様な明白な結果が得られなかった一方で、”理解への一歩”という点では前進があった。
”この僅かな前進でも悲観してはいない”とケドラヤは言う。
”もっと期待はしてましたが、少なくとももう一度カンファレンスを開催し、更に先へ進む事ができるかを確認する価値はある”
一方で、自身の研究について望月教授に詳しく説明する責任があると考える人もいる。
ファルティングスはメールで、”個人的には、望月氏自身が皆が理解できる論文を書かなければ解決しないという印象を受けた”と書いている。
しかしキムは、その必要があるとは考えていない。
”参加者が抱いた困惑は、よい困惑であり、何かを学んでる最中に訪れるものだ。このカンファレンスに先立ち、殆どの参加者が論文に書かれた望月教授の試みに関して予備知識が足りなかったようです”とキムは語った。
”先週のカンファレンスではみな戸惑っていましたが、望月教授がやろうとしてる事の概要は掴めたと思う。どうしたらそれを完全に理解ができるのか?ただ疑問は増えたが、1つ1つがより洗練されたのは疑いようがないのです”
以上、”WIRED Papers from Inter Universe”からでした。
最後に
2012年、数学界に激震が走った。30年近く誰も解けなかった「ABC予想」を京都大学教授の望月新一が証明したというのだ。
ただ、その証拠である論文は”異世界からきた”と思われるほど難解で誰にも理解できなかった・・・
それから3年の時を経て、数学界最大の謎に立ち向かうべく、イギリスでカンファレンスが昨年開かれた。そこで一体何が起きたのか?
WIREDは当時、この日本人の偉業をド派手に書き立てた。勿論、その気持ちも理解できる。しかし、現実は甘くはなかった。
どんなに素晴らしい発見も理論も、相手に伝わらなければ、相手が理解してくれなければ、藻屑と消え去るのも、数学史の冷酷な掟でもある。
リーマンの僅か6頁の論文は、理解するのに30年、証明するのに10年掛かった。その論文の途中にある、リーマンが”粗雑”と切り捨てたリーマン予想は未だ解決に至ってはいない。
一方でアーベルの関数論は、”500年分の仕事を数学者に遺してくれた”と言わしめた。
数学界に激震が走った2012年から8年を経て、再び同じ様な激震が日本中を走った。
今度は、”証明した”とされる論文が査読を通過し、京大数理解析研究所が刊行する専門誌「PRIMS」に掲載される事が決定したのだ。
個人的には査読に7年も掛ったんだから、これから専門チームによる本格的厳密な検証を受ける事になるが、ABC予想の完全証明は意外に早いような気もするが。
いやそう思うのは私だけであろうか。










一方で、多項式についても同様なABC予想を考えると、冪指数も係数も不要な不等式(ディオファントス幾何的な不等式)が成立します。この不等式も転んだサンが説明されてますね。
多項式は複素数の範囲で考えると、常に1次式の積に分解されますが、これを素因数分解と同様に考えれば、前述の”rad”が定義されます。
そこで多項式の場合は、n次多項式とm次多項式の和の次数は、nとmの大きい方を超える事はないので(フェルマーの定理より)、話は極めて単純になります。他方、整数の場合は和をとると、その素因数分解は全く違ったものになるから、大変ややこしくなります。
多項式に置き換えると、証明の見通しが良くなるとはこの事ですね。朝早くから余計な補足でした。
私もうっかりしてました。
フェルマーの定理を複素数の多項式バージョンで証明すると、多項式の次数の積が不等式で表現され、とても楽なんですよね。
ABC予想も同様に楕円曲線という複素数の多項式に変換すれば、証明の見通しがずっと明るくなるんです。ただ、変換する時の復元の誤差が面倒だか。
貴重な補足とても参考になります。
リーマンがリーマン予想において完全対称のゼータであるクシー関数を新たに定義したのも証明の見通しをよくする為でした。
望月教授がABC予想において、整数論を幾何学と群論を経由し多項式に置き換えたのも殆ど同じような理由からです。
一日も早く正式にこの証明が受理される事を期待したい。
リーマン予想の時は、アダマールがクシー関数の”積表示”を証明してくれたから明示公式もめでたく証明できたんですが。
ABC予想の証明もアダマールみたいな助っ人が必要かもです。
コメントとっても参考になります。
逆を言えば、フェルマーの定理の多項式バージョンが解ければ、ABC予想は簡単に解けるんだろうか?
フェルマー予想の多項式版の証明は、1879年にRリュービルという人が既にこのやり方で証明してます。実際に数Ⅲレベルで証明できます。私には難しかったですが(悲)。
ABC予想➡フェルマー定理は可能ですが、逆は無理っぽみたいですね。
どんなもんやろか?
”(f(t)ⁿ+g(t)ⁿ=1(n≧3)”の矛盾を導き出すんですが、リーマン面を例にとって種数を計算すると矛盾が出るとかで。
簡単というより凄く抽象的にも思えますが、これもブログに立てたいと思います(予定)。
幾何に変換してしまえば、群を経由し代数学から導き出される不等式はほとんど誤差がないので一気にABC予想の矛盾を不等式の形で導き出せるんだが。
結局一番のネックはこの幾何学への変換理論なんだろうが。
数論を幾何に変換すると、口では簡単に言えますが。とても危険な計算なんですよね。
一度、幾何に変換してしまえば後はスムーズ?なんでしょうが。
考えるほどに混乱しますね。
貴重なコメント何時も有難うです。