リーマン予想と素数の謎と”旧4の1”〜ゼータ関数の謎と3種の解析接続

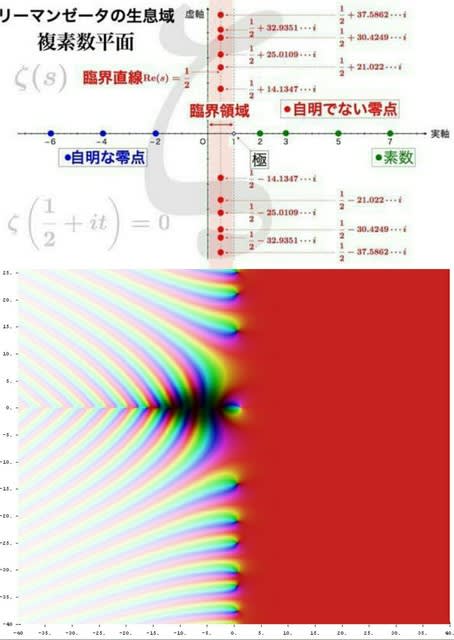
　上の図は､複素数平面(xy座標)におけるリーマンゼータ関数を色で表現(白いほど発散し､黒いほどゼロに)してます。
　横軸xが複素数sの実部Re(s)で､縦軸yが虚部Im(s)です。色軸がリーマンゼータ関数ζ(s)の値です。つまり､この図は複素平面とζ(s)値の3次元空間を表してます。
　よく見ると､x=1/2の縦軸上(虚部軸)に､朧気な黒い点､つまり､ζ(s)=0なる”零点”が並んでます。
　この縦に並んだ飛び飛びの黒い点列が"自明でない"零点であり､x<0(負)でy=0の横軸上(実部軸)の明らかに黒い点群(負の偶数)が"自明な"零点(ζ(−2)=ζ(−4)=· · ·=0)です。

　ここで､"自明"とか"自明でない"とか出てきますが､実数部の線上(横軸)に存在するのが"自明"で､虚数部の線上(縦軸)に存在するのが"非自明”です。
　英語では､自明なゼロを"the trivial zeros"と言います。因みに､自明な零点(ζ(−2)=ζ(−4)=· · ·=0)を実零点(実根)､非自明な零点(ζ(s)=0)を虚零点(虚根)とも言います。
　また､s=1における白い点は極(無限遠)で､ゼータ関数を零点と極に関する無限積に分解した結果､ゼータ関数には素数に関する分解と､零点と極に対する分解という2つの表示が得られました。　
　右下の小さな図にある様に､自明でないx=1/2上の虚零点はζ(s)=ζ(1/2+yi)=0となり､y=±14.13...､±21.02...､±25.01...､±30.42...､±32.93...である事が判ってます。

与えられた数より小さい素数の個数

　1859年､33歳のリーマンは､手書きの僅か8ページの論文で､｢与えられた数より小さい素数の個数について｣を発表する。
　この短い論文中に､"ζ(s)の自明でないゼロ点は､全ての複素平面上で､実部が1/2の直線上に存在する"と予想する(結果だけで証明はしていない)1行を含んでいた。　
　そして､その論文の中に非常に興味深い記述があった。
　”実際､この領域内に､ほぼこれと同じ位多くの実根があり､しかも､それらの根が全て実根である事は極めて確かだと思われる。
　勿論､その厳密な証明が望まれるが。私の粗雑な計算をしてはみたが､期待した程の成果は得られなかった。よって､この証明には触れないでおく事にした。
　何故なら､私のこの素数定理を作る為には､その証明は必要ないと思えたからだ”

　この論文の記述こそが後に､多くの数学者を悩ませる事となる｢リーマン予想｣であり､これこそが”リーマンの謎”なんです。この”粗雑な計算式”の証明を論文の中で紹介してたら､ひょっとしたら今頃はリーマンの謎が解けてたかもです。
　リーマン予想を有り体に言えば､ζ(s)=0となるゼータ関数の”自明でない”全ての零点sの実部Re(s)は1/2となるですね。

3種の解析接続

　この論文中でリーマンは､”x以下の素数の個数”を導く明示公式(素数公式)を導出した。素数の個数関数π(x)をゼータ関数ζ(s)を用いて表示する精度の高い解析公式で､リーマンの主張は不完全でしたが､フォン･マンゴルドにより証明されます(1895年)。
　それ以外にも､”2種類の解析接続”も発表した(本当は3つ)。1つ目は､”1の3”でも述べたガンマ関数Γを用いた”オイラーの第1積分表示”で､これを使い､リーマンは第1の解析接続を進めます。
　2つ目は､”1の4”と”1の5”でも詳しく述べてますが。テータ関数θを用いた”リーマンの第2積分表示”を使い､第二の解析接続を進めます。因みに､この第2の積分表示は､完全対称な関数等式が保型性から得られるもので､保系形式•保型表現のゼータ関数へと大きく発展します。

　そして3つ目。これが凄い事になるんです。”リーマン-シーゲル公式”というもので､1932年､リーマンの大学の後輩であるシーゲル(Carl Ludwig Siegel､独､1896-1981)が､ゲッチンゲン大学に保存してあった､リーマンの計算メモを発見。ゼータ関数の第3の積分表示から､解析接続を行った。
　リーマンは､このゼータの第3の表示と解析接続には相当の自信を持ってた様で､零点の詳細な研究が出来ると見込んでました。
　実際､リーマンはゼータ関数の幾つかの虚零点にては､実部が1/2となるのを手計算で求め､リーマン予想の確認をしてた程で､最初の零点が､1/2+i*14.134725141734...という超精密なものでした。

ゼータの完全対称等式

　この短い論文に含まれてる謎はこれだけじゃない。
　リーマンが､この論文の中で発表した非対称型関数等式ζ(s)=2ˢπˢ⁻¹sin(πs/2)Γ(1−s)ζ(1−s)に､ガンマ因子”(√π)⁻ˢΓ(s/2)”を掛け､完備ゼータ関数”ξ(s)=(√π)⁻ˢΓ(s/2)ζ(s)”を作ると､完全対称型の関数等式”ξ(s)=ξ(1−s)”を満たす(”1の6”参照)。
　このガンマ因子を補った完備ゼータ関数がゼータ関数の本来の姿である事を提示しました。そして､この完備ゼータ関数に完全対称な美が伴ってる事が､数学史上初めて証明されたんです。
　そして､この関数等式こそがありとあらゆるゼータ関数に結び付き､大きく拡張されていく。

　ゼータ関数の日本の第一人者でもある黒川信重氏は解説する。"リーマンが知りたかったのは､素数そのものを精密に求める素数の解析公式(明示公式)だった。これを成立させるには､素数の情報を内蔵するゼータ関数がどこでゼロになるか？という根の分布の研究が必須だった"

　リーマンの1859年の論文の真の貢献はその結果ではなく､その方法にある。
　リーマンの明示公式に関する最も重要な結果は､その主要項が対数積分”∫[2,x]dt/logt”であると主張した。しかし､この主張に関するリーマンの証明は不十分だった。
　一方でリーマンの方法には､ゼータ関数ζ(s)を複素関数として扱い､ζ(s)の複素数に関する(虚)零点の研究､フーリエ反転公式やメビウス反転公式､素数定理π(x)の解析公式としての提示が含まれており､こうした全ての研究は､リーマン予想の解決よりも大きな成果をもたらしました(｢ゼータ関数とリーマン予想｣より)。