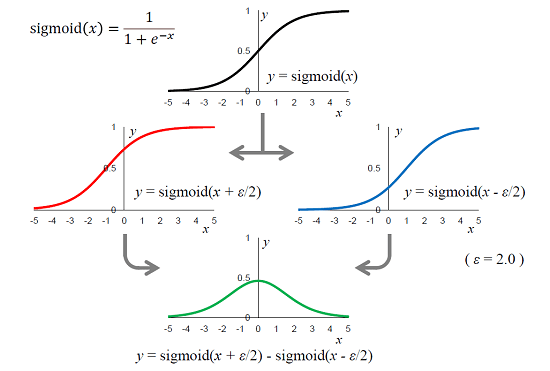
ニューラルネットワークで多く用いられるシグモイド関数を組み合わせると、三角関数のような波形を作り出すことができます。次の図のように、基準となるシグモイド関数(黒)を、x軸方向に正の方向(青)と負の方向(赤)にそれぞれ平行移動して、その両者を線形結合(重ね合わせ)することで、新たな単発パルス波形(緑)が得られます。
さて、「フーリエ級数展開」で知られるように、一般的に「任意の関数は三角関数の線形結合で表現(近似)できる」ので、上記のシグモイド関数(緑)の波形でも同様のことができるかも知れません。そこで、三角関数の波形とシグモイド関数の単発パルス波形の重ね合わせにより、それぞれ矩形波の近似関数を作ってみました。
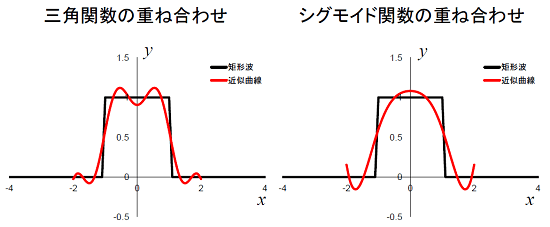
左が三角関数を5つ重ねた波形、右が単発パルス波形を5つ重ねた波形(シグモイド関数は10個に相当)です。右(シグモイド関数)の場合は、左(三角関数)ほどではないにせよ、それなりに「矩形波」を表現(近似)しています。なお、適用区間は「-2≦x≦2」に限定しています。
ここで、重ね合わせに用いた波形(成分)を列挙してみましょう。まず、三角関数については、下記の5種類の関数を重ね合わせました。
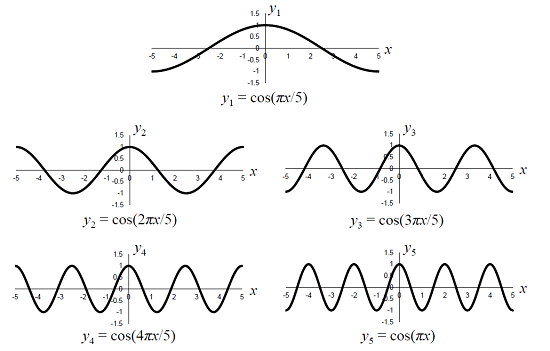
続いて、シグモイド関数については、下記の5種類の単発パルス波形を重ね合わせました。
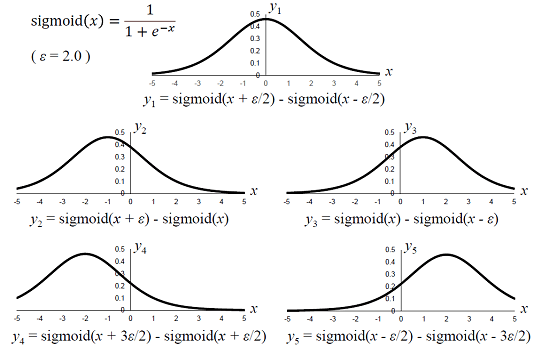
従って、シグモイド関数を幾つも重ね合わせることで(線形結合)、近似関数を作り出すことができます。
ニューラルネットワークでは、多くのシグモイド関数を段階的に重ね合わせることで、その関数近似能力を高めているのです。しかも、機械学習のプロセスにおいては、個々のシグモイド関数の重みを「自動的に」調節しているのです。

さて、「フーリエ級数展開」で知られるように、一般的に「任意の関数は三角関数の線形結合で表現(近似)できる」ので、上記のシグモイド関数(緑)の波形でも同様のことができるかも知れません。そこで、三角関数の波形とシグモイド関数の単発パルス波形の重ね合わせにより、それぞれ矩形波の近似関数を作ってみました。

左が三角関数を5つ重ねた波形、右が単発パルス波形を5つ重ねた波形(シグモイド関数は10個に相当)です。右(シグモイド関数)の場合は、左(三角関数)ほどではないにせよ、それなりに「矩形波」を表現(近似)しています。なお、適用区間は「-2≦x≦2」に限定しています。
ここで、重ね合わせに用いた波形(成分)を列挙してみましょう。まず、三角関数については、下記の5種類の関数を重ね合わせました。

続いて、シグモイド関数については、下記の5種類の単発パルス波形を重ね合わせました。
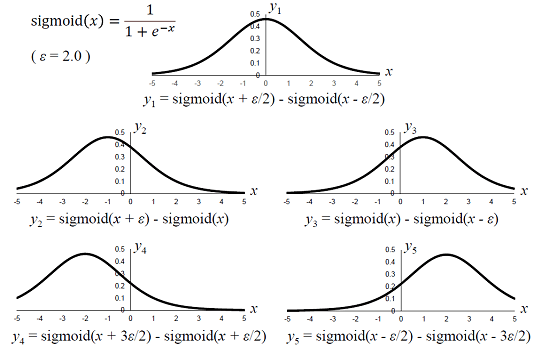
従って、シグモイド関数を幾つも重ね合わせることで(線形結合)、近似関数を作り出すことができます。
ニューラルネットワークでは、多くのシグモイド関数を段階的に重ね合わせることで、その関数近似能力を高めているのです。しかも、機械学習のプロセスにおいては、個々のシグモイド関数の重みを「自動的に」調節しているのです。

















