実はここ数年、集合住宅の居室内で携帯電話の電波の不調が目立つようになりました。高層ビルが「雨後の筍」の如く周囲に出現していることも一つの要因ではないか、そうだとすると物理学的な背景は何か?と考えています(そもそも、電波環境の良い所に引っ越しを検討する方が先かも)。
そこで、ここ最近は電磁気学を勉強し直しています。工学部(但し「機械系」)で電磁気学を履修したのは、約四半世紀前の大学1年(教養部)の頃です。当時は「ベクトル解析」に不慣れなことに加え、「電場と電束」「磁場と磁束」の概念を混同しておりました。改めて学び直すことで、ようやくイメージが掴めてきました。
電磁気学の諸現象は「マクスウェル方程式」から出発して導くことができます。そして、この「マクスウェル方程式」とは電磁気に関する次の4つの方程式から構成されます。

(1)(2)は各々「電場と磁場の特徴」について記述しており、(3)(4)は「電場と磁場の相互作用」について記述しています。
この記事では、マクスウェル方程式の「イメージ」を概観した後、電磁波の「波動方程式」を導き出します。より深い専門知識については、多くのサイトで解説されているので、ここでは割愛します。
(1)電場に対するガウスの法則
電気を帯びた物体があると、その周りでは電気的な力(静電気力)が働く空間が生成されます。この空間のことを「電場(電界)」と言います。電場の強さは、その影響によって生じる電気的な力(静電気力)のベクトル量で表されます。
電気には正(+)と負(-)の2種類の電荷があり、電場によって生じる力は正から負の向きに働きます。この分布を図で表したのが電気力線や電束線です。いずれも「+極」より出でて「-極」に至るのが特徴です。そして、正(+)と負(-)は各々単独の電荷(モノポール)として存在できます。
これらの線は途中で枝分かれすることは無く、また互いに交わることもありません。また、正(+)の電荷からは線が湧き出し、負(-)の電荷によって吸い込まれます。この様子を簡単に表したイメージが下の図です。さらに、電荷の絶対値が大きくなるにつれて、湧き出しや吸い込みの対象となる線の本数は増加します。
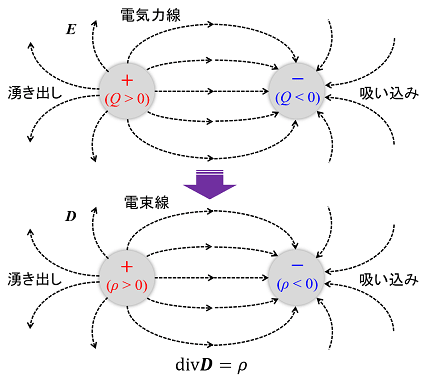
正(+)と負(-)の2つの電荷を左右に置くと、正(+)の電荷から電気力線(電束線)が湧き出し、負(-)の電荷に吸い込まれます。電気力線や電束線を描くことで、電荷の周囲に現れた電場の分布が可視化されます。
しかし、この図だけでは「電場(電気力線)」と「電束(電束線)」の違いが判りません。そもそも、学生時代を振り返っても、電場については「電気力線」で説明されることがほとんどで、「電束線」を使った記憶がありません。
そこで、こんなことを考えてみましょう。一様な電場の中に(帯電していない)物体を挿入した場合、物体内ではどのような電気的な変化を生じるのか。
平行平板状の電極を用意して「左側を正(+)、右側を負(-)」に設定すると、極板間では左→右の向きに一様な電場を生じます。この中に、未だ帯電していない物体を挿入します。

ここで、物体を構成する物質には「電気を通しやすいもの(導体)」と「通しにくいもの(絶縁体)」があります。従って、2つの場合を考える必要があります。
もし、挿入する物体が「導体」の場合は、物体内の負電荷キャリア(自由電子)が左側、正電荷キャリアが右側に引き寄せられることで物体表面が帯電します(静電誘導)。これに伴って、物体内部では「右→左」の向きに電場を生成し、外部から加わる電場と相殺します。この結果、両者の電場は打ち消し合うため、物体内部では「電場を生じない」状態が作り出されます。
一方、挿入する物体が「絶縁体」の場合は、物体を構成する各分子内で負電荷が左側、正電荷が右側に少しずつ偏ることで、全体で電気的な偏り(分極ベクトル)を生じます(誘電分極)。これに伴って、物体内部では「右→左」の向きに弱い電場を生成し、外部から加わる電場と相殺します。この結果、物体内部では「外部から加わる電場」が幾分弱まった状態で作用し続けます(これがコンデンサーでは重要な意味を持ちます→「誘電体」)。
いずれの場合でも、物体の内部と外部では「電場の扱い」が異なります。簡単に言えば「物体の表面を境に、電気力線の本数が変わる」ということです。
そこで、物体の内部と外部でシームレスに扱える物理量として考えられるのが「電束」です。真空中であろうとも、物質中であろうとも、その特性(物性)の違いを「誘電率ε」で吸収することで、シームレスに扱うことができます。つまり、「物体の表面を境に、電束線の本数は変わらない」ということです。ある種の「保存量」のように扱えるような、「利便性」があると言っても良いでしょう。
(2)磁場に対するガウスの法則
磁気を帯びた物体(例えば永久磁石)があると、その周りでは磁気的な力(磁力)が働く空間が生成されます。この空間のことを「磁場(磁界)」と言います。磁場の強さは、その影響によって生じる磁気的な力(磁力)のベクトル量で表されます。
磁気にはN極(+)とS極(-)の2種類の磁荷があり、磁場によって生じる力はN極からS極の向きに働きます。この分布を図で表したのが磁力線や磁束線です。
これらの線は途中で枝分かれすることは無く、また互いに交わることもありません。さらに、磁荷の絶対値が大きくなるにつれて、線の本数は増加します。この様子を簡単に表したイメージが下の図です。

ここで、磁力線は「N極」より出でて「S極」に至るのに対して、磁束線は閉曲線となっています。これは、電荷とは異なり、「N極」と「S極」各々単独の磁荷(モノポール)として存在できないことに起因します。この図を見ると「磁束」の方が、物体の内部と外部をシームレスに扱う物理量として適しています。
それでは、「磁場(磁力線)」と「磁束(磁束線)」の違いは何でしょう。この点を明らかにするために、こんなことを考えてみましょう。一様な磁場の中に(磁気を帯びていない)物体を挿入した場合、物体内ではどのような磁気的な変化を生じるのか。
幅の広い永久磁石を2本用意し「一方の右端がN極、他方の左端がS極」となるように向かい合わせ、間隔を開けて設置します。この時、2つの磁石の間では左→右の向きに一様な磁場を生じます。この中に、未だ磁気を帯びていない物体を挿入します。その後、挿入された物質は、磁場に晒される内に磁気を帯び(磁石の性質を持ち)始めます(磁化)。

ここで、磁化に伴って「物体に生じる磁場」の向きによって、物体は「強磁性体」「常磁性体」「反磁性体」の3つの種類に分けられます。ここで、物体に生じる磁場のS極からN極に向かって「磁気分極」というベクトルを生じます。これが磁化の強さを示すものです。
強磁性体と常磁性体の場合、磁気分極の向きは「物体外部の磁場の向きと同じ」です。この場合、物体に現れる磁場は「外部磁石のN極と向き合う側の表面でS極、外部磁石のS極と向き合う側の表面でN極」となるような向きとなります。このため、物体は外部磁石に吸い寄せられます。
一方、反磁性体の場合、磁気分極の向きは「物体外部の磁場の向きと逆向き」です。この場合、物体に現れる磁場は「外部磁石のN極と向き合う側の表面でN極、外部磁石のS極と向き合う側の表面でS極」となるような向きとなります。このため、物体は外部磁石に反発します。
いずれの場合でも、物体の内部と外部では「磁場の扱い」が異なります。簡単に言えば「物体の表面を境に、磁場の様子が変わる」ということです。そこで、物体の内部と外部でシームレスに扱える物理量として考えられるのが「磁束」です。
つまり、「物体の表面を境に、磁束の様子や磁束線の本数は変わらない」ということです。真空中であろうとも、物質中であろうとも、その特性(物性)の違いを「透磁率μ」で吸収することで、シームレスに扱うことができます。
(3)ファラデーの電磁誘導の法則
磁束が時間とともに変化すると、その磁束を囲むような電場(誘導電流)が誘起されるというものです。中学校の理科でも「コイルに磁石を近づけたり、遠ざけたりする実験」でお馴染みですね。
例えば、磁束が上向きから下向きに変化すると、その周りを取り巻くように反時計回りの電場が発生します。また、磁束が下向きから上向きに変化すると、その周りを取り巻くように時計回りの電場が発生します。
磁束密度はベクトルBで表されます。この時間変化を反転したものが、生成される電場ベクトルの回転(rot)に相当します。ベクトルの回転は「相対渦度」を思い浮かべるとイメージしやすいでしょう。

なお、電流(電流密度j)と電場(電場E)の間には、「j=σE」の関係(一般化されたオームの法則)があります(σは電気伝導率)。
(4)アンペールの法則
続いては、電流(電場)の周りで、その電流を囲むような磁場が誘起されるというものです。そして、この電流には「伝導電流」と「変位電流」の2種類があります。
通常の電気回路で「電流」と呼ばれるものは、(切れて無い)導線を伝わる「伝導電流」です。中学校の理科でも「直線電流の周りに磁場を生じる」ことを学びますが、この電流も「伝導電流」です。このような電流は、電流密度jで表します。
ここで新たに登場するのが「変位電流」です。例えば、コンデンサーのような平行平板状の電極を考えてみます。この極板間は空洞ですので、導線としては「切断」されています。

この両側に「直流」の電圧を加えると、短い時間の中で「極板間には電場を生じ、極版には電荷が蓄積」されます。しかし、その後何もしなければ、電荷の移動は生じません。つまり、電荷の移動という点では「膠着状態」です。
一方、両側に「交流」の電圧を加えると、短い時間の中で「極板間には電場を生じ、極版には電荷が蓄積」されます。さらに、電圧や電流の大きさや向きは時間と共に周期変動します。つまり、極板間の電場(電束)が周期変動を繰り返すことになります。これに伴い、蓄電と放電が交互に繰り返されるため、(極板間は切断されているにも関わらず)その両側では電荷の移動が持続することになります(変位電流)。これが電流としての役割を果たし、その周囲に磁場を生じさせるのです。
以上が、電磁場の基礎方程式である「マクスウェル方程式」のイメージです。
真空中の電磁波
それでは、マクスウェルの方程式から「電磁波の支配方程式(波動方程式)」を導いてみましょう。今回は「真空中」を伝わる電磁波について考えてみます。外部に電荷や電流が存在しないため、電荷密度や電流密度は全てゼロとして扱うことが可能です。

マクスウェル方程式の他に、構成方程式が3つあります。これは電束密度と電場、磁束密度と磁場、電流密度と電場を各々関係付けるものです。これらの式に真空中の諸条件を適用して、真空中のマクスウェル方程式を導きます。ここで、方程式のパラメータは電場Eと磁場Hで揃えておきます。
続いて、電場の回転(∇×E)の式の両辺に回転の演算(∇×)を施します。左辺はベクトル3重積の要領で展開し、電場の発散の式(∇・E=0)を適用することで、電場Eのラプラシアンを得ます。右辺は磁場の回転(∇×H)の式を適用することで、電場の2階時間微分に導くことができます。この両者を合わせると、電場の波動方程式が得られます。
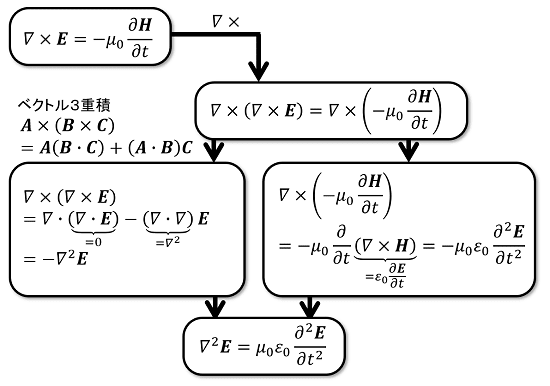
また、同様にして、磁場の波動方程式も得られます。

こちらの記事では、さらに電磁波の特性にクローズアップしていきます。
そこで、ここ最近は電磁気学を勉強し直しています。工学部(但し「機械系」)で電磁気学を履修したのは、約四半世紀前の大学1年(教養部)の頃です。当時は「ベクトル解析」に不慣れなことに加え、「電場と電束」「磁場と磁束」の概念を混同しておりました。改めて学び直すことで、ようやくイメージが掴めてきました。
電磁気学の諸現象は「マクスウェル方程式」から出発して導くことができます。そして、この「マクスウェル方程式」とは電磁気に関する次の4つの方程式から構成されます。

(1)(2)は各々「電場と磁場の特徴」について記述しており、(3)(4)は「電場と磁場の相互作用」について記述しています。
この記事では、マクスウェル方程式の「イメージ」を概観した後、電磁波の「波動方程式」を導き出します。より深い専門知識については、多くのサイトで解説されているので、ここでは割愛します。
(1)電場に対するガウスの法則
電気を帯びた物体があると、その周りでは電気的な力(静電気力)が働く空間が生成されます。この空間のことを「電場(電界)」と言います。電場の強さは、その影響によって生じる電気的な力(静電気力)のベクトル量で表されます。
電気には正(+)と負(-)の2種類の電荷があり、電場によって生じる力は正から負の向きに働きます。この分布を図で表したのが電気力線や電束線です。いずれも「+極」より出でて「-極」に至るのが特徴です。そして、正(+)と負(-)は各々単独の電荷(モノポール)として存在できます。
これらの線は途中で枝分かれすることは無く、また互いに交わることもありません。また、正(+)の電荷からは線が湧き出し、負(-)の電荷によって吸い込まれます。この様子を簡単に表したイメージが下の図です。さらに、電荷の絶対値が大きくなるにつれて、湧き出しや吸い込みの対象となる線の本数は増加します。

正(+)と負(-)の2つの電荷を左右に置くと、正(+)の電荷から電気力線(電束線)が湧き出し、負(-)の電荷に吸い込まれます。電気力線や電束線を描くことで、電荷の周囲に現れた電場の分布が可視化されます。
しかし、この図だけでは「電場(電気力線)」と「電束(電束線)」の違いが判りません。そもそも、学生時代を振り返っても、電場については「電気力線」で説明されることがほとんどで、「電束線」を使った記憶がありません。
そこで、こんなことを考えてみましょう。一様な電場の中に(帯電していない)物体を挿入した場合、物体内ではどのような電気的な変化を生じるのか。
平行平板状の電極を用意して「左側を正(+)、右側を負(-)」に設定すると、極板間では左→右の向きに一様な電場を生じます。この中に、未だ帯電していない物体を挿入します。

ここで、物体を構成する物質には「電気を通しやすいもの(導体)」と「通しにくいもの(絶縁体)」があります。従って、2つの場合を考える必要があります。
もし、挿入する物体が「導体」の場合は、物体内の負電荷キャリア(自由電子)が左側、正電荷キャリアが右側に引き寄せられることで物体表面が帯電します(静電誘導)。これに伴って、物体内部では「右→左」の向きに電場を生成し、外部から加わる電場と相殺します。この結果、両者の電場は打ち消し合うため、物体内部では「電場を生じない」状態が作り出されます。
一方、挿入する物体が「絶縁体」の場合は、物体を構成する各分子内で負電荷が左側、正電荷が右側に少しずつ偏ることで、全体で電気的な偏り(分極ベクトル)を生じます(誘電分極)。これに伴って、物体内部では「右→左」の向きに弱い電場を生成し、外部から加わる電場と相殺します。この結果、物体内部では「外部から加わる電場」が幾分弱まった状態で作用し続けます(これがコンデンサーでは重要な意味を持ちます→「誘電体」)。
いずれの場合でも、物体の内部と外部では「電場の扱い」が異なります。簡単に言えば「物体の表面を境に、電気力線の本数が変わる」ということです。
そこで、物体の内部と外部でシームレスに扱える物理量として考えられるのが「電束」です。真空中であろうとも、物質中であろうとも、その特性(物性)の違いを「誘電率ε」で吸収することで、シームレスに扱うことができます。つまり、「物体の表面を境に、電束線の本数は変わらない」ということです。ある種の「保存量」のように扱えるような、「利便性」があると言っても良いでしょう。
(2)磁場に対するガウスの法則
磁気を帯びた物体(例えば永久磁石)があると、その周りでは磁気的な力(磁力)が働く空間が生成されます。この空間のことを「磁場(磁界)」と言います。磁場の強さは、その影響によって生じる磁気的な力(磁力)のベクトル量で表されます。
磁気にはN極(+)とS極(-)の2種類の磁荷があり、磁場によって生じる力はN極からS極の向きに働きます。この分布を図で表したのが磁力線や磁束線です。
これらの線は途中で枝分かれすることは無く、また互いに交わることもありません。さらに、磁荷の絶対値が大きくなるにつれて、線の本数は増加します。この様子を簡単に表したイメージが下の図です。

ここで、磁力線は「N極」より出でて「S極」に至るのに対して、磁束線は閉曲線となっています。これは、電荷とは異なり、「N極」と「S極」各々単独の磁荷(モノポール)として存在できないことに起因します。この図を見ると「磁束」の方が、物体の内部と外部をシームレスに扱う物理量として適しています。
それでは、「磁場(磁力線)」と「磁束(磁束線)」の違いは何でしょう。この点を明らかにするために、こんなことを考えてみましょう。一様な磁場の中に(磁気を帯びていない)物体を挿入した場合、物体内ではどのような磁気的な変化を生じるのか。
幅の広い永久磁石を2本用意し「一方の右端がN極、他方の左端がS極」となるように向かい合わせ、間隔を開けて設置します。この時、2つの磁石の間では左→右の向きに一様な磁場を生じます。この中に、未だ磁気を帯びていない物体を挿入します。その後、挿入された物質は、磁場に晒される内に磁気を帯び(磁石の性質を持ち)始めます(磁化)。

ここで、磁化に伴って「物体に生じる磁場」の向きによって、物体は「強磁性体」「常磁性体」「反磁性体」の3つの種類に分けられます。ここで、物体に生じる磁場のS極からN極に向かって「磁気分極」というベクトルを生じます。これが磁化の強さを示すものです。
強磁性体と常磁性体の場合、磁気分極の向きは「物体外部の磁場の向きと同じ」です。この場合、物体に現れる磁場は「外部磁石のN極と向き合う側の表面でS極、外部磁石のS極と向き合う側の表面でN極」となるような向きとなります。このため、物体は外部磁石に吸い寄せられます。
一方、反磁性体の場合、磁気分極の向きは「物体外部の磁場の向きと逆向き」です。この場合、物体に現れる磁場は「外部磁石のN極と向き合う側の表面でN極、外部磁石のS極と向き合う側の表面でS極」となるような向きとなります。このため、物体は外部磁石に反発します。
いずれの場合でも、物体の内部と外部では「磁場の扱い」が異なります。簡単に言えば「物体の表面を境に、磁場の様子が変わる」ということです。そこで、物体の内部と外部でシームレスに扱える物理量として考えられるのが「磁束」です。
つまり、「物体の表面を境に、磁束の様子や磁束線の本数は変わらない」ということです。真空中であろうとも、物質中であろうとも、その特性(物性)の違いを「透磁率μ」で吸収することで、シームレスに扱うことができます。
(3)ファラデーの電磁誘導の法則
磁束が時間とともに変化すると、その磁束を囲むような電場(誘導電流)が誘起されるというものです。中学校の理科でも「コイルに磁石を近づけたり、遠ざけたりする実験」でお馴染みですね。
例えば、磁束が上向きから下向きに変化すると、その周りを取り巻くように反時計回りの電場が発生します。また、磁束が下向きから上向きに変化すると、その周りを取り巻くように時計回りの電場が発生します。
磁束密度はベクトルBで表されます。この時間変化を反転したものが、生成される電場ベクトルの回転(rot)に相当します。ベクトルの回転は「相対渦度」を思い浮かべるとイメージしやすいでしょう。

なお、電流(電流密度j)と電場(電場E)の間には、「j=σE」の関係(一般化されたオームの法則)があります(σは電気伝導率)。
(4)アンペールの法則
続いては、電流(電場)の周りで、その電流を囲むような磁場が誘起されるというものです。そして、この電流には「伝導電流」と「変位電流」の2種類があります。
通常の電気回路で「電流」と呼ばれるものは、(切れて無い)導線を伝わる「伝導電流」です。中学校の理科でも「直線電流の周りに磁場を生じる」ことを学びますが、この電流も「伝導電流」です。このような電流は、電流密度jで表します。
ここで新たに登場するのが「変位電流」です。例えば、コンデンサーのような平行平板状の電極を考えてみます。この極板間は空洞ですので、導線としては「切断」されています。

この両側に「直流」の電圧を加えると、短い時間の中で「極板間には電場を生じ、極版には電荷が蓄積」されます。しかし、その後何もしなければ、電荷の移動は生じません。つまり、電荷の移動という点では「膠着状態」です。
一方、両側に「交流」の電圧を加えると、短い時間の中で「極板間には電場を生じ、極版には電荷が蓄積」されます。さらに、電圧や電流の大きさや向きは時間と共に周期変動します。つまり、極板間の電場(電束)が周期変動を繰り返すことになります。これに伴い、蓄電と放電が交互に繰り返されるため、(極板間は切断されているにも関わらず)その両側では電荷の移動が持続することになります(変位電流)。これが電流としての役割を果たし、その周囲に磁場を生じさせるのです。
以上が、電磁場の基礎方程式である「マクスウェル方程式」のイメージです。
真空中の電磁波
それでは、マクスウェルの方程式から「電磁波の支配方程式(波動方程式)」を導いてみましょう。今回は「真空中」を伝わる電磁波について考えてみます。外部に電荷や電流が存在しないため、電荷密度や電流密度は全てゼロとして扱うことが可能です。

マクスウェル方程式の他に、構成方程式が3つあります。これは電束密度と電場、磁束密度と磁場、電流密度と電場を各々関係付けるものです。これらの式に真空中の諸条件を適用して、真空中のマクスウェル方程式を導きます。ここで、方程式のパラメータは電場Eと磁場Hで揃えておきます。
続いて、電場の回転(∇×E)の式の両辺に回転の演算(∇×)を施します。左辺はベクトル3重積の要領で展開し、電場の発散の式(∇・E=0)を適用することで、電場Eのラプラシアンを得ます。右辺は磁場の回転(∇×H)の式を適用することで、電場の2階時間微分に導くことができます。この両者を合わせると、電場の波動方程式が得られます。

また、同様にして、磁場の波動方程式も得られます。

こちらの記事では、さらに電磁波の特性にクローズアップしていきます。

















