8年前に「円筒座標系の熱流体方程式と熱ロスビー波」という記事を掲載しました。今回はこの記事の続報になります。前回は数値計算のプログラムをFortranで作成しましたが、今回はこのプログラムをC#に移植して数値実験を行いました。
さて、傾圧不安定波を実験で再現する取り組みとしては、回転水槽を用いた研究が有名です。一般的な回転水槽のイメージを次の図に示します。
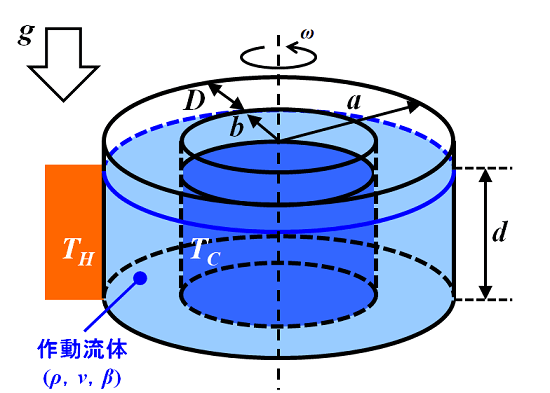
これは(北極に見立てた)中心部を氷等で冷やす一方、(赤道に見立てた)外側から加熱された(中緯度地方に見立てた)回転二重円筒間の流れを観察するものです。この時、実験装置全体は一定の各速度で回転しています。半径方向の温度勾配や回転速度(角速度)に応じて、流れの様子が変化(波動の形成される様子)します。
これに対して、私が開発している数値モデルのイメージは次の図のようなものです。

半径方向に温度勾配を与えられながら、一定の回転角速度で回転し続ける二重円筒形状容器を考え、その内部に充填された試験流体(気体)の熱流動を考えます。
ここで、作動流体を「水」ではなく「気体」としたのは、これまで局地風のような気流の数値シミュレーションを扱ってきたので、その延長上の取り組みであるためです。実は、閉鎖空間の中に充填させると考えた方がモデルを組みやすいのです。
初期条件と境界条件は過去の記事と同様です。
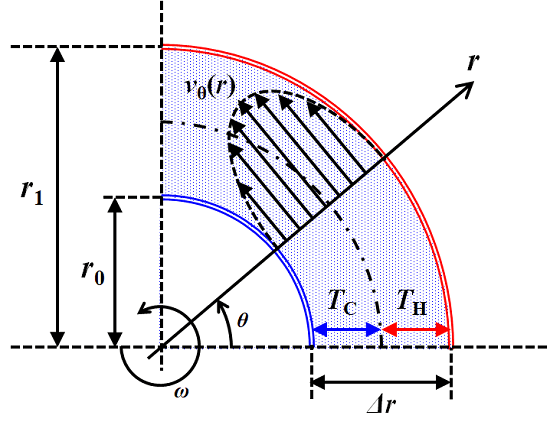
初期条件としては、内側半分の温度をTC、外側半分の温度をTHとし、速度分布は壁面上を0、半径方向の中心を極大とする放物状としました。また、境界条件としては、壁の両側では摩擦により速度は0とし、温度はTHまたはTCに等しいものとしました。
数値シミュレーションに際して見るべき箇所は次の図のように4つの断面を設定しました。
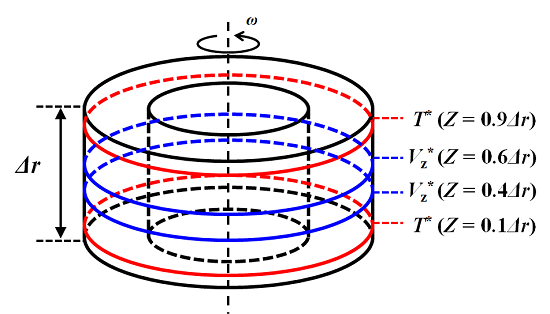
今回は、上層(Z=0.9Δr)と下層(Z=0.1Δr)の温度分布、および中層付近(Z=0.6Δr,Z=0.4Δr)の速度の鉛直成分を見ることにしました。
それでは、数値シミュレーションの結果の一例を次の図に示します。
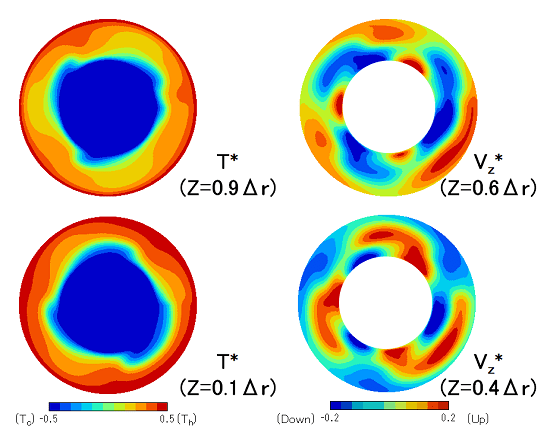
左側は温度分布(赤・高温、青・低温)、右側は鉛直速度(赤・上昇流、青・下降流)です。また、上の段は上層側、下の段は下層側です。
温度分布をみると、上層・下層共に3つの波動が形成されています。また、互いに位相がずれて様子が見られます。鉛直速度を見ると、温度分布で見られた波動に伴って上下に動く様子が現れています。上層と下層で上昇流と下降流が互いに逆転しつつ、その位置(位相)が互いにずれている様子も見られます。
パラメータの条件を変えることで、色々な波動の様子やその鉛直構造を解析することができそうです。
さて、傾圧不安定波を実験で再現する取り組みとしては、回転水槽を用いた研究が有名です。一般的な回転水槽のイメージを次の図に示します。

これは(北極に見立てた)中心部を氷等で冷やす一方、(赤道に見立てた)外側から加熱された(中緯度地方に見立てた)回転二重円筒間の流れを観察するものです。この時、実験装置全体は一定の各速度で回転しています。半径方向の温度勾配や回転速度(角速度)に応じて、流れの様子が変化(波動の形成される様子)します。
これに対して、私が開発している数値モデルのイメージは次の図のようなものです。

半径方向に温度勾配を与えられながら、一定の回転角速度で回転し続ける二重円筒形状容器を考え、その内部に充填された試験流体(気体)の熱流動を考えます。
ここで、作動流体を「水」ではなく「気体」としたのは、これまで局地風のような気流の数値シミュレーションを扱ってきたので、その延長上の取り組みであるためです。実は、閉鎖空間の中に充填させると考えた方がモデルを組みやすいのです。
初期条件と境界条件は過去の記事と同様です。

初期条件としては、内側半分の温度をTC、外側半分の温度をTHとし、速度分布は壁面上を0、半径方向の中心を極大とする放物状としました。また、境界条件としては、壁の両側では摩擦により速度は0とし、温度はTHまたはTCに等しいものとしました。
数値シミュレーションに際して見るべき箇所は次の図のように4つの断面を設定しました。

今回は、上層(Z=0.9Δr)と下層(Z=0.1Δr)の温度分布、および中層付近(Z=0.6Δr,Z=0.4Δr)の速度の鉛直成分を見ることにしました。
それでは、数値シミュレーションの結果の一例を次の図に示します。
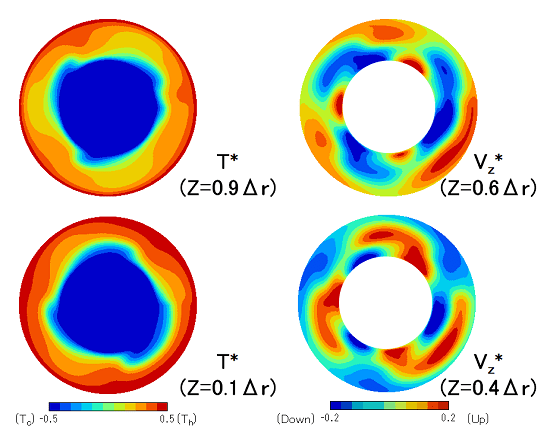
左側は温度分布(赤・高温、青・低温)、右側は鉛直速度(赤・上昇流、青・下降流)です。また、上の段は上層側、下の段は下層側です。
温度分布をみると、上層・下層共に3つの波動が形成されています。また、互いに位相がずれて様子が見られます。鉛直速度を見ると、温度分布で見られた波動に伴って上下に動く様子が現れています。上層と下層で上昇流と下降流が互いに逆転しつつ、その位置(位相)が互いにずれている様子も見られます。
パラメータの条件を変えることで、色々な波動の様子やその鉛直構造を解析することができそうです。

















