難問

　夏休み、中２の塾生の数学の宿題で質問された問題がどうしても分からなかった。まったく恥ずかしい話だが、私立中学校の宿題は時々難問が出されて苦労することがある。それでも今までは何とか解答を捻り出してきたものだが、今回だけはお手上げ状態だった。それはこんな問題だ。

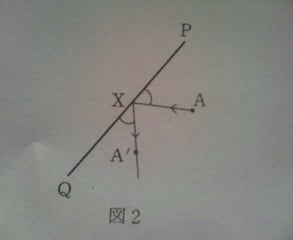
（問い）　下の図１のように、平面上に３辺ＰＱ，ＱＲ，ＲＰからなる枠がある。今、この枠の中で球を転がして枠に反射させ、球が転がって行く様子を観察することにする。球は枠に衝突する前も衝突した後も、まっすぐに転がる。また、下の図２のように、点Ａから辺ＰＱ上の点Ｘをめがけて球を転がすと、球は∠ＰＸＡ＝∠ＱＸＡ'となるように、反射して転がっていく。
　
　
　このとき次の各問いに答えよ。ただし作図に利用した線は消さないで残しておくこと。
（１）下の図３において、点Ａから球を転がして辺ＰＱ上の点に衝突させた後、点Ｂを通過させたい。球が点Ａから点Ｂまで転がったあとを作図せよ。


（２）上の図１において、点Ａから球を転がして辺ＰＱ，ＱＲ，ＲＰの順に衝突させて反射させ、再び点Ａを通過するようにしたい。球が点Ａから辺ＰＱ，ＱＲ，ＲＰに、それぞれ衝突して点Ａまで転がったあとを作図せよ。

　（１）の問題は何度も作図したことがあるのですぐにできた。


書き方は
　①Ａから直線ＰＱに垂線を引き、ＰＱとの交点をＨとする。
　②ＰＱに関してＡの反対側に、Ａ'Ｈ＝ＡＨとなる点をとる。
　③２点Ａ'，Ｂを結び、ＰＱとの交点をＸとし、ＡとＸを結ぶ。
このとき、２つの線分ＡＸ，ＸＢが求めるあとである。
（これでいい理由は、∠ＡＸＰ＝∠Ａ'ＸＰ、∠Ａ'ＸＰ＝∠ＢＸＱであるから、∠ＡＸＰ＝∠ＢＸＱが成り立つから）

　だが、（２）がどうやっても思いつかない。もちろん（１）の書き方を応用すればいいのだが、どうやったらいいのかまったく見当がつかない。普段なら色々調べて答えを見つけられるが、夏休み中ではそんな時間もなく、分からないまま徒に日が過ぎていってしまった。だが、決して忘れたわけではなく、何度も考えてみたのだが、どうにも閃かない。もともと数学のセンスに乏しい私であるから、こうなってしまうとどうにもならないのは自覚しているが、生徒の手前投げ出すわけにもいかない。あれこれ粘ってみたのだが、結局分からないまま夏休みが終わってしまい、「ごめん、とうとう分からなかった。答えをもらったら見せてね」と謝るしかなかった。屈辱的だが、できないものは正直に認めなければいけない。
　２学期が始まって少ししたら、その生徒が学校で配られた解答を持って来てくれた。それを見て、「なるほど！」と思わずうなってしまったが、やはり私にはとても思いつけないものだったと素直に認めざるを得なかった。だが、もし万一同じ問題をいつか見かけたら、今度は同じ失敗を繰り返さないように以下にその解答を書き留めておこうと思う。　

（解)　直線ＰＱ，ＰＲに関して、点Ａと対称な点を、それぞれＡ'，Ａ''とし、直線ＱＲに関して、Ａ''と対称な点をＡ'''とする。また、Ａ'Ａ'''とＰＱ，ＱＲとの交点を、それぞれＸ，Ｙとし、ＹＡ''とＰＲとの交点をＺとする。このとき（１）と同様に考えると、
　∠ＡＸＰ＝∠ＹＸＱ，　∠ＸＹＱ＝∠ＺＹＲ，　∠ＹＺＲ＝∠ＡＺＰ
が成り立つから、点Ａから点Ｘに向けて球を転がすと、Ｙ，Ｚで反射して、球は再びＡに戻る。


　
　(反省)　点ＡのＰＱ，ＱＲ，ＲＰに関する対称な点をそれぞれとって、その３点を結んでしまったのが混乱の原因。まったく頭が固くていやになる・・。