人生の答えは１つじゃない〜円周等分方程式と約数と因数分解の奇妙な関係

　”入試問題の正解は1つだが､人生には正解が幾つもある”
　これは｢ドラゴン桜｣の桜木先生(阿部寛)の言葉だという事を､あるフォロワーの記事で知った。
　”解が幾つもある”と聞いて､円周を等分する方程式であるxⁿ−1をふと思い出した。
　数学の巨人ガウスに言わせると､xⁿ−1=0は円をn等分するからn個の解があると。
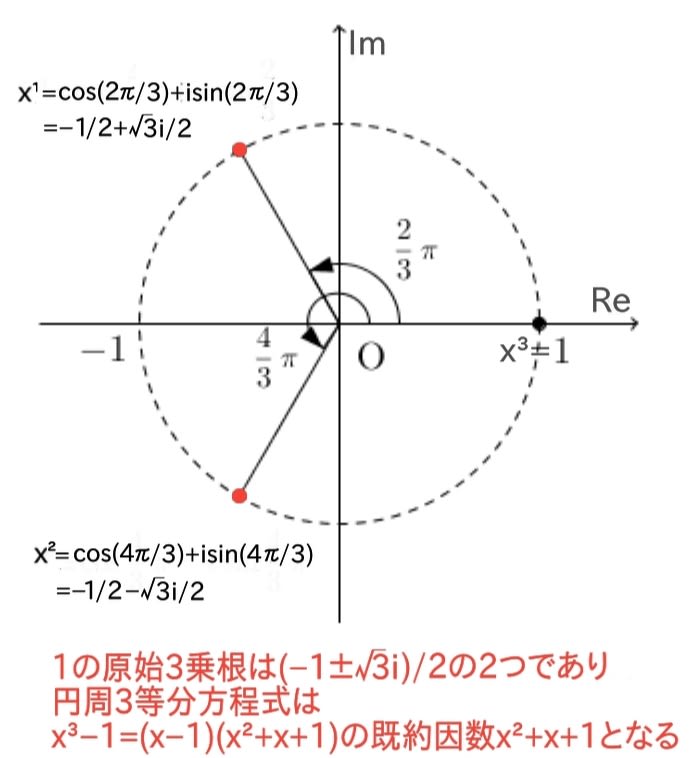
　確かに､x²−1=(x−1)(x+1)=0は､x=±1で円を2等分し､x³−1=(x−1)(x²+x+1)=0は､x=1とx=(−1±√3i)/2で円を3等分する(上図)。

　こうして見れば､人生の答えが我らの周りを等間隔に無数に並んでると思えば､人生も満更悪くはない気がする。しかし､人生も数学も思うほどに単純じゃない。
　x⁴−1=(x²−1)(x²+1)=(x−1)(x+1)(x²+1)と分解できる所までは簡単だが､x⁵−1となると数学に慣れてる人以外は､x⁴+x³+x²+x+1が円を5等分する円分方程式だと一目で見抜くのは難しいだろう。
　つまり､x⁵−1=(x−1)(x⁴+x³+x²+x+1)と分解できるからだ。もっと数学に慣れてる人なら､x⁴+x³+x²+x+1がそれ以上(因数)分解できない事を。そしてもっともっと慣れてる人は､アイゼンシュタインという数学者を思い出すだろう。彼が発見した”既約の法則”を使えば､これ以上因数分解できない事が判るからだ。

円周等分方程式の誕生　

　xⁿ−1を(整数係数の既約)因数分解した時に現れる､ある既約多項式を円周等分方程式(円分方程式)いう。
　nが2以外の素数では､xⁿ−1=(x−1)(xⁿ⁻¹+xⁿ⁻²+･･･+x²+x+1)が成立し､既約因数xⁿ⁻¹+xⁿ⁻²+･･･+x²+x+1を円周等分多項式という。
　ガウス的に言えば､xⁿ−1=0の事も”円の等分割を定める方程式”と呼ぶ。
　xⁿ−1=0の解は､cos(2kπ/n)+isin(2kπ/n)､(k=1,2,…,n)と複素数根の形で表示されますが､(cosθ+isinθ)ⁿ=cos(nθ)+isin(nθ)というドモアブルの定理から即座に導き出せ､ガウス以前から知られてました。

　円分方程式のn個の複素数根はn乗すると1(1のn乗根)になるが､これらのn個の根を複素平面(ガウス平面)上で表すと､単位円周上をn等分する点になり､それらを直線で結ぶと円に内接する正n角形ができる。故に､円周等分多項式と呼ぶ。
　オイラー研究で有名な高瀬正仁サン的に言い換えると､正多角形の作図という幾何の問題は､円分方程式の根を求めるという代数方程式の問題に帰着する。また､根の実部と虚部はsin関数とcos関数の形で表示され､円関数である三角関数と円分方程式との関連も見て取れる。
　更に､オイラーの公式(eⁱᶿ=cosθ+isinθ)を使えば､円分方程式の解はe^(2πik/n)で示される。
　つまり､ガウスは円周等分方程式の解を複素指数関数の特殊値として表示した。しかしガウスの真意は数論にあり､円分方程式の解を用いて､平方剰余相互法則に結びつけます。

　ガウスが創造した円周等分方程式論は実に不思議な理論で､異質な幾つもの側面が一同に共有されます。
　複素変数関数論と代数方程式論と幾何の作図問題と数論が円周等分方程式の舞台で一堂に会し､密な関係で結ばれている。ガウスはそんな神秘的な光景を当り前の様に見る事のできる眼力の持ち主でした。
　ベルヌイもオイラーもガウスも得体の知れない複素数に戸惑い､尻込みする数学者が多かった中で､何の躊躇もなく正面から堂々と複素数を語っていました。
　彼らは人生に答えがなかったとしても堂々と人生を語り続けたでしょうね。
　

原始n乗根と円分方程式

　上述したガウスの解の表示を使えば､1の3乗根は､cos(2kπ/3)+isin(2kπ/3)となり､k=1,2,3について計算した(−1+√3i)/2と(−1−√3i)/2と1の3つの根を繋ぐと正三角形になる(上図)。　
　そこで1のn乗根のうち､x=cos(2π/n)+isin(2π/n)のべきx¹,x²,x³,…を順につくれば､n乗して初めて1になるものがある。この様に､n乗して初めて1になる複素数を”1の原始n乗根”という。

　例えば1の6乗根は､x¹=(1+√3i)/2､x²=(−1+√3i)/2､x³=−1､x⁴=(−1−√3i)/2､x⁵=(1−√3i)/2､x⁶=1の6つだが､{(−1±√3i)/2}³=1､(±1)²=1であるから､(−1±√3i)/2と±1の4つは､1の6乗根であっても原始6乗根ではない。
　また､(1±√3i)/2は6乗して初めて1になるから1の原始6乗根である。つまり､6と互いに素な1と5のべき乗根となる。
　故に､1のn乗根xᵏ=cos(2πk/n)+isin(2πk/n)が1の原始n乗根になる為の必要十分条件は､kとnが互いに素である事が解る。
　1の原始6乗根x¹とx⁵は､x⁶−1=(x−1)(x+1)(x²+x+1)(x²−x+1)の既約因数x²−x+1の根であり､円周6等分方程式はx²−x+1となる。
　同様に､1の原始3乗根は(−1±√3i)/2であり､円周3等分方程式はx³−1=(x−1)(x²+x+1)の既約因数x²+x+1となる。

　実際に､xⁿ−1の因数分解をnが1から12までについてやってみる。
　x²−1=(x−1)(x+1)
　x³−1=(x−1)(x²+x+1)
　x⁴−1=(x−1)(x+1)(x²+1)
　x⁵−1=(x−1)(x⁴+x³+x²+x+1)
　x⁶−1=(x−1)(x+1)(x²+x+1)(x²−x+1)
　x⁷−1=(x−1)(x⁶+x⁵+x⁴+x³+x²+x+1)
　x⁸−1=(x−1)(x+1)(x⁴+1)　
　x⁹−1=(x−1)(x²+x+1)(x⁶+x³+1)
　x¹⁰−1=(x−1)(x+1)(x⁴+x³+x²+x+1)(x⁴−x³+x²−x+1)
　x¹¹−1=(x−1)(x¹⁰+x⁹+x⁸+x⁷+x⁶+x⁵+x⁴+x³+x²+x+1)
　x¹²−1=(x−1)(x+1)(x²+1)(x²−x+1)(x⁴−x²+1)

　これを見れば判る様に､xⁿ−1の因数分解はnが大きくなるより､nの約数が多い程に分解される因子も多くなる。
　但し､ 係数が0か±1しか出てこない事に気付いた貴方は流石です。しかし､n=105の時に係数−2が登場し､n=385では絶対値3の項も登場。後はスパコンでの計算ですが､n=40755で絶対値100の係数が､n=40755では絶対値57から342が初めて登場する事が知られてます。

　そこで､nの約数の数とxⁿ−1の因子の数を比較してみます。
n=2､約数の数=2､xⁿ−1の因子の数=2　
n=3､約数の数=2､xⁿ−1の因子の数=2 　
n=4､約数の数=3､xⁿ−1の因子の数=3
n=5､約数の数=2､xⁿ−1の因子の数=2
n=6､約数の数=4､xⁿ−1の因子の数=4
n=7､約数の数=2､xⁿ−1の因子の数=2
n=8､約数の数=4､xⁿ−1の因子の数=4
n=9､約数の数=3､xⁿ−1の因子の数=3
n=10､約数の数=4､xⁿ−1の因子の数=4
n=11､約数の数=2､xⁿ−1の因子の数=2
n=12､約数の数=5､xⁿ−1の因子の数=5

　見事に､nの約数の数=xⁿ−1の因子数となってますね。
　そこでxⁿ−1を因数分解した時の最高次数を見てみますが､nが素数の時､n−1となってます。それに､nの約数が多い程少ない。
　そこで､nと互いに素なn以下の自然数の数φ(n)と最高次数を比べます。
　因みに､φ(n)はオイラーのφ関数で､”互いに素”とは､共通の約数が1だけ(最大公約数が1)で､例えばn=10の時の互いに素な自然数は1,3,7,9の4つとなる。すると
　n=2､φ(2)=1､最高次数=1
　n=3､φ(3)=2､最高次数=2
　n=4､φ(4)=2､最高次数=2
　n=5､φ(5)=4､最高次数=4
　n=6､φ(6)=2､最高次数=2
　n=7､φ(7)=6､最高次数=6
　n=8､φ(8)=4､最高次数=4
　n=9､φ(9)=6､最高次数=6
　n=10､φ(10)=4､最高次数=4
　n=11､φ(11)=10､最高次数=10
　n=12､φ(12)=4､最高次数=4

　つまり､xⁿ−1を因数分解した時の因子の数はnの約数と一致し､因子の最高次数はφ(n)である事が判る。この様に､xⁿ−1の因数分解とnの素因数分解は密に関わってますね。
　xⁿ−1=0の解は勿論､n乗して1になりますが。上述した様に､この1のn乗根の中で”n乗して初めて1になる”ものを”原始n乗根”と呼びます。xⁿ−1=0の中で､”原始n乗根”のみを解とするものを円周等分方程式(円分多項式)といい､Φₙ(x)で示す。
　n=12までの例で言えば､
　Φ₁=x−1
　Φ₂=(x²−1)/Φ₁=x+1
　Φ₃=(x³−1)/Φ₁=x²+x+1
　Φ₄=(x⁴−1)/Φ₁Φ₂=x²+1
　Φ₅=(x⁵−1)/Φ₁=x⁴+x³+x²+x+1
　Φ₆=(x⁶−1)/Φ₁Φ₂Φ₃=x²−x+1
　Φ₇=(x⁷−1)/Φ₁=x⁶+x⁵+x⁴+x³+x²+x+1
　Φ₈=(x⁸−1)/Φ₁Φ₂Φ₄=x⁴+1
　Φ₉=(x⁹−1)/Φ₁Φ₃=x⁶+x³+1
　Φ₁₀=(x¹⁰−1)/Φ₁Φ₂Φ₅=x⁴−x³+x²−x+1
　Φ₁₁=(x¹¹−1)/Φ₁=x¹⁰+x⁹+x⁸+x⁷+x⁶+x⁵+x⁴+x³+x²+x+1
　Φ₁₂=(x¹²−1)/Φ₁Φ₂Φ₃Φ₄Φ₆=x⁴−x²+1

　そこで､nを奇素数p(2を除く素数)とする時､1の原始n乗根はφ(p)=p−1個ある。
　一方､xᵖ−1=(x−1)(xᵖ⁻¹+xᵖ⁻²+･･･+x²+x+1)のxᵖ⁻¹+xᵖ⁻²+･･･+x²+x+1=0はp−1次式より､この解は全て1の原始n乗根である事が判る。
　故に､Φₚ(x)=xᵖ⁻¹+xᵖ⁻²+･･･+x²+x+1となる。勿論これは､Φₙ(x)が既約(な多項式)であるという前提が必要ですが。
　但し､既約である為には､アイゼンシュタインの(既約)判定法を使います。これは整数係数多項式がある3つの条件を満たせば既約になるというもので､定理自体は単純ですが､証明は難しいのでここでは省きます。

　故に”既約”を前提とすれば､xⁿ−1の因数分解は簡単に導き出せます。
　例えばn=10の時､10の約数は10,5,2,1の4つで､1の10乗根は1の原始10乗根と原始5乗根と原始2乗根と原始1乗根からなり､これらは重複しない。
　つまり､x¹⁰−1=Φ₁Φ₂Φ₅Φ₁₀となる。k=1,2,5,10(10の約数)とすると､1の原始k乗根はφ(k)個あるので､上述した様にxⁿ−1の円分多項式の(最高)次数はφ(n)に等しいから､Φₖ(x)の次数はkである事が判る。
　故に､x¹⁰−1=(x−1)(x+1)(x⁴+x³+x²+x+1)(x⁴−x³+x²−x+1)と因数分解できる。
　これは､n=12でも同じで､12の約数は1,2,4,6,12より､x¹²−1=Φ₁Φ₂Φ₄Φ₆Φ₁₂=(x−1)(x+1)(x²+1)(x²−x+1)(x⁴−x²+1)となる。

　つまり､何をいいたいのか？
　これこそが､”約数さえ判れば円周等分多項式は簡単に解ける”という見事なトリックなんですね。

　ガウスは何故､数学という難題塗れの人生を優雅に堂々と歩めたのか？
　それは､難題の裏側に広がる雄大な背景を見抜く鋭い洞察眼と､数学という複雑多岐に組み合わさった魔術(トリック)とアイデアを併せ持ってたからでしょうか。
　ガウスは数学の教授にはなりませんでした。もし彼が教授になってたら､”人生には正解が幾つもある様に思える。しかし､数学と同じで人生にも最適解というものは存在しない。だが､数学には人生と同じく無限の可能性がある。それに､その可能性の奥には美しい光景が広がってる”とでも言ったでしょうか。
　ガウスの円周等分方程式を眺めてる内に､ふとそう思ってしまう自分がいる。

　因みに､私がドラゴン桜の先生だったら､以下の様な説教を垂れるかもしれない。

　”人生には数学と同じで最適解は存在しない。だが､その最適解を探し出そうとするその姿勢が尊く､美しいのだ”と。