今回は「連続体力学」の話題です。固体も流体も、力学的には「連続体」として統一的に扱うことができます。なお、この記事では「専門書」のような厳密かつ精密な理論展開ではなく、ざっくりとした「思考の流れ」を扱います。
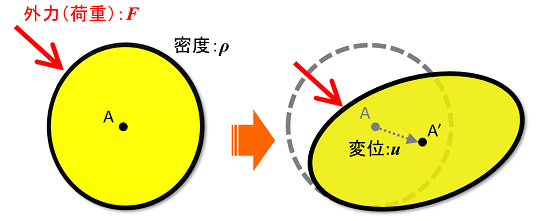
まずは、ある物質の塊を考えてみます。さらにこの塊に外から力(外力・荷重)Fを加えてみた所、変形しました。そんな状況をイメージしてみましょう。

この変形した塊の内部では、外力Fとは異なる力(内力)が分布しています。塊を仮想的に切断してみると、その切断面上では様々な内力Pが分布しています。
この中のほんの一部(ΔA)に着目すると、このわずかな面積に対してわずかな内力(ΔP)が作用しています。この時の「面積に対する内力」のことを応力と言います。もう少し詳しく見てみましょう。

微小面積ΔAに対する微小内力ΔPの向き(角度)は、切断面の取り方によって変わります。そこで、微小内力ΔPを成分分解します。つまり、微小面積ΔAに対して垂直な方向(法線方向)と切断面に沿う方向(接線方向)です。
この各成分ΔPnとΔPtをΔAで割り、ΔA→0の極限をとったものが、垂直応力σn、およびせん断応力σtとなります。
この概念をもう少し拡張して考えてみましょう。塊全体を考えるに当たって、まずはそのごく一部だけを取り出して考えることにします。この取り出した部分を「微小片」と言います。

微小片に対して、座標系を設定します。ここでは「x軸、y軸」に替えて「x1軸、x2軸」を使用します(便宜上)。また、簡単のため「2次元問題」として考えてみます。従って、奥行の大きさは一律で「1」(単位長さ)とします。
微小片に働く応力を考えてみます。応力は微小片の外周(切断面)上に作用するものと考えます。また、応力には垂直応力とせん断応力の2種類が存在します。ここで、応力は「σij」の形で表記されます。i軸をぶった切る方向の面に対してj軸の方向に作用する応力という意味です。

垂直応力(σ11、σ22)は各面に対して垂直に作用する一方、せん断応力(σ12、σ21)は各面を擦る(または、滑る)ように作用します。図中の「×」が作用点です。
ここで、微小片が勝手に回転することは無いので、せん断応力σ12とσ21は等しくなります(せん断応力σ12とσ21に伴うモーメントは常に釣り合います)。
また、これらの応力に伴って、微小片に働くx1軸とx2軸方向の力(=応力×面積)を右側の青枠に記載しました。いきなり微分記号(∂)が登場していますが、これは下記の近似を使用したためです。

続いては、「ひずみ」について考えてみます。微小片に応力が働くと変形を生じます。そこで、「元の長さ」に対する「長さの変化」の割合を「ひずみ」と言います。

まずは垂直ひずみを考えてみましょう。
垂直応力σ11が働くことで、x1軸方向の長さがΔu1だけ変化します。また、垂直応力σ22が働くことで、x2軸方向の長さがΔu2だけ変化します。
それぞれ、元の長さに対する変化の割合(さらに元長さ→0の極限)を求めて、ε11とε22が決まります(右側青枠)。

続いて、せん断ひずみを考えてみましょう。
せん断応力σ21が働くことで、x1軸方向の面がΔu1だけシフトします。これに伴い、元長さΔx2の面が角度θ1だけ傾きます。
また、せん断応力σ12が働くことで、x2軸方向の面がΔu2だけシフトします。これに伴い、元長さΔx1の面が角度θ2だけ傾きます。
それぞれ、元の長さに対するシフト長さの割合(さらに元長さ→0の極限)を求めて、角度θ1とθ2が決まります。θ1とθ2を足して2で割ったものとして、ε21とε12は定義されます(図中青枠)。
ここで、2つの変位(Δu1とΔu2)から3つのひずみ(ε11、ε22、ε21=ε12)が決まります。と、言うことは3つのひずみの間には何らかの関係があるはずです。
そこで、せん断ひずみε12の式を、x1とx2で順次微分してみます。

こうして、3つのひずみの関係が明らかになりました(図中青枠)。この関係を「ひずみの適合条件式」と言います。
微小片に働く力(応力)と変形(ひずみ)について考えてきましたので、今度は移動(速度・加速度)について考えてみましょう。速度は変位の時間変化で定義されます。また、速度は位置(x1、x2)と時間(t)の関数です。

上の図のように、時間Δtの間に点Aが点A’まで移動する場合を考えてみます。速度が時間Δtでの変化量、すなわち加速度を求めてみましょう。

速度が位置(x1、x2)と時間(t)の関数であることに着目すると、加速度は時間微分項に非線形項が加わった形で表されます。但し、速度が遅い場合、また変位勾配が小さい場合には非線形項は無視できる程度に小さいと近似することができます。
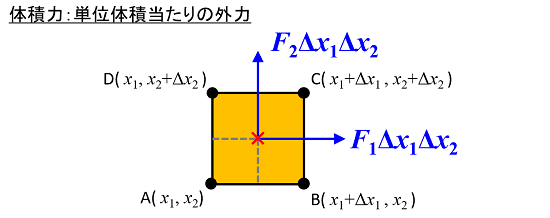
最後に、塊全体を取り巻く環境条件を考慮することを考えましょう。例えば、重力場における重力、電磁場における電磁力などの影響です。このような環境(外界)の影響によって作用する力を、単位体積当たりに働く力として考慮し、これを体積力(物体力)と言います。
ここまでの結果を用いて、x1軸方向、およびx2軸方向の運動方程式を立ててみましょう。

以上の内容を、アインシュタインの縮約記法(総和規約)を用いて一般化すると次のように表されます。記事の中では2次元問題として扱いましたが、一般化することで3次元問題への適用も容易になります。

さて、ここまで微小片に働く力(応力)と変形(ひずみ)、移動(速度・加速度)を考察し、運動方程式を導出してきました。しかし、ここまで「この塊」が「固体」であるか「流体」であるかについては明確にしてきませんでした。つまり、ここまでの内容は固体・流体を問わず適用可能と言うことです。
それでは、「固体」と「流体」の性質はどのように反映させるのでしょうか。実は「固体」と「流体」の性質を決める方程式は、また別に存在します。それは応力とひずみを結びつける「構成方程式」です。
例えば、「固体」の場合は次のような構成方程式を適用します。

これを応用することで、「弾性体の変形解析」を行うことができます。
また、「流体」の場合は次のような構成方程式を適用します。

上記の応力で表示した運動方程式に、こちらの構成方程式と連続の式を適用すると、粘性流体の運動方程式である「ナビエ・ストークス方程式」が導出されます。これを応用することで、例えば「建造物の通風・換気シミュレーション」を行うことができます。
このような技術が、さらに「地域気象の計算シミュレーション」にまで発展します。

まずは、ある物質の塊を考えてみます。さらにこの塊に外から力(外力・荷重)Fを加えてみた所、変形しました。そんな状況をイメージしてみましょう。

この変形した塊の内部では、外力Fとは異なる力(内力)が分布しています。塊を仮想的に切断してみると、その切断面上では様々な内力Pが分布しています。
この中のほんの一部(ΔA)に着目すると、このわずかな面積に対してわずかな内力(ΔP)が作用しています。この時の「面積に対する内力」のことを応力と言います。もう少し詳しく見てみましょう。

微小面積ΔAに対する微小内力ΔPの向き(角度)は、切断面の取り方によって変わります。そこで、微小内力ΔPを成分分解します。つまり、微小面積ΔAに対して垂直な方向(法線方向)と切断面に沿う方向(接線方向)です。
この各成分ΔPnとΔPtをΔAで割り、ΔA→0の極限をとったものが、垂直応力σn、およびせん断応力σtとなります。
この概念をもう少し拡張して考えてみましょう。塊全体を考えるに当たって、まずはそのごく一部だけを取り出して考えることにします。この取り出した部分を「微小片」と言います。

微小片に対して、座標系を設定します。ここでは「x軸、y軸」に替えて「x1軸、x2軸」を使用します(便宜上)。また、簡単のため「2次元問題」として考えてみます。従って、奥行の大きさは一律で「1」(単位長さ)とします。
微小片に働く応力を考えてみます。応力は微小片の外周(切断面)上に作用するものと考えます。また、応力には垂直応力とせん断応力の2種類が存在します。ここで、応力は「σij」の形で表記されます。i軸をぶった切る方向の面に対してj軸の方向に作用する応力という意味です。

垂直応力(σ11、σ22)は各面に対して垂直に作用する一方、せん断応力(σ12、σ21)は各面を擦る(または、滑る)ように作用します。図中の「×」が作用点です。
ここで、微小片が勝手に回転することは無いので、せん断応力σ12とσ21は等しくなります(せん断応力σ12とσ21に伴うモーメントは常に釣り合います)。
また、これらの応力に伴って、微小片に働くx1軸とx2軸方向の力(=応力×面積)を右側の青枠に記載しました。いきなり微分記号(∂)が登場していますが、これは下記の近似を使用したためです。

続いては、「ひずみ」について考えてみます。微小片に応力が働くと変形を生じます。そこで、「元の長さ」に対する「長さの変化」の割合を「ひずみ」と言います。

まずは垂直ひずみを考えてみましょう。
垂直応力σ11が働くことで、x1軸方向の長さがΔu1だけ変化します。また、垂直応力σ22が働くことで、x2軸方向の長さがΔu2だけ変化します。
それぞれ、元の長さに対する変化の割合(さらに元長さ→0の極限)を求めて、ε11とε22が決まります(右側青枠)。

続いて、せん断ひずみを考えてみましょう。
せん断応力σ21が働くことで、x1軸方向の面がΔu1だけシフトします。これに伴い、元長さΔx2の面が角度θ1だけ傾きます。
また、せん断応力σ12が働くことで、x2軸方向の面がΔu2だけシフトします。これに伴い、元長さΔx1の面が角度θ2だけ傾きます。
それぞれ、元の長さに対するシフト長さの割合(さらに元長さ→0の極限)を求めて、角度θ1とθ2が決まります。θ1とθ2を足して2で割ったものとして、ε21とε12は定義されます(図中青枠)。
ここで、2つの変位(Δu1とΔu2)から3つのひずみ(ε11、ε22、ε21=ε12)が決まります。と、言うことは3つのひずみの間には何らかの関係があるはずです。
そこで、せん断ひずみε12の式を、x1とx2で順次微分してみます。

こうして、3つのひずみの関係が明らかになりました(図中青枠)。この関係を「ひずみの適合条件式」と言います。
微小片に働く力(応力)と変形(ひずみ)について考えてきましたので、今度は移動(速度・加速度)について考えてみましょう。速度は変位の時間変化で定義されます。また、速度は位置(x1、x2)と時間(t)の関数です。

上の図のように、時間Δtの間に点Aが点A’まで移動する場合を考えてみます。速度が時間Δtでの変化量、すなわち加速度を求めてみましょう。

速度が位置(x1、x2)と時間(t)の関数であることに着目すると、加速度は時間微分項に非線形項が加わった形で表されます。但し、速度が遅い場合、また変位勾配が小さい場合には非線形項は無視できる程度に小さいと近似することができます。
最後に、塊全体を取り巻く環境条件を考慮することを考えましょう。例えば、重力場における重力、電磁場における電磁力などの影響です。このような環境(外界)の影響によって作用する力を、単位体積当たりに働く力として考慮し、これを体積力(物体力)と言います。

ここまでの結果を用いて、x1軸方向、およびx2軸方向の運動方程式を立ててみましょう。

以上の内容を、アインシュタインの縮約記法(総和規約)を用いて一般化すると次のように表されます。記事の中では2次元問題として扱いましたが、一般化することで3次元問題への適用も容易になります。

さて、ここまで微小片に働く力(応力)と変形(ひずみ)、移動(速度・加速度)を考察し、運動方程式を導出してきました。しかし、ここまで「この塊」が「固体」であるか「流体」であるかについては明確にしてきませんでした。つまり、ここまでの内容は固体・流体を問わず適用可能と言うことです。
それでは、「固体」と「流体」の性質はどのように反映させるのでしょうか。実は「固体」と「流体」の性質を決める方程式は、また別に存在します。それは応力とひずみを結びつける「構成方程式」です。
例えば、「固体」の場合は次のような構成方程式を適用します。

これを応用することで、「弾性体の変形解析」を行うことができます。
また、「流体」の場合は次のような構成方程式を適用します。

上記の応力で表示した運動方程式に、こちらの構成方程式と連続の式を適用すると、粘性流体の運動方程式である「ナビエ・ストークス方程式」が導出されます。これを応用することで、例えば「建造物の通風・換気シミュレーション」を行うことができます。
このような技術が、さらに「地域気象の計算シミュレーション」にまで発展します。

















