それにしても・・・高校の世界史は、なかなか覚えられませんね(やっぱり、理系なんだな・・・)。古代ギリシャとローマの区別がつきにくかったり、とにかく舌を噛みそうなカタカナ言葉が多いです。その一方で、古代中国では難しい漢字ばかりでやっぱり紛らわしい・・・何とか覚えたのが、古代インド・マウリア朝のアショーカ王・・・だけ(爆)。
そういえば、ブログではここ2~3日、珍しく真面目に気象学の記事を書いているので(←本来はいつもそうあるべきなのですが)・・・ついでに?、大気の運動方程式についても触れておきましょう。
今回は、局地気象ではなく・・・むしろ局地気象に支配的な影響を及ぼす、北半球規模での大規模スケールの運動を考えてみましょう。図1のように北半球上に原点をとり、直交座標系を設定します。

図1.北半球上に設置された直交座標系
直交座標系内のある一部の空気の塊についての運動方程式は次のように表すことができます。
(x軸方向:東西方向) ρ(du/dt)=-(∂p/∂x)+ρfv+Fx
(y軸方向:南北方向) ρ(dv/dt)=-(∂p/∂y)+ρfu+Fy
(z軸方向:鉛直方向) ρ(dw/dt)=-(∂p/∂z) +Fz-ρg
ここで
(du/dt)=(∂/∂t)+u(∂/∂x)+v(∂/∂y)+w(∂/∂z)
f=2Ωsinφ
地球上の大気には、気圧傾度力、コリオリの力、摩擦力、重力の4つの力が働いています。コリオリの力とは、地球の自転に伴う慣性力で、進行方向の右向きに働きます。
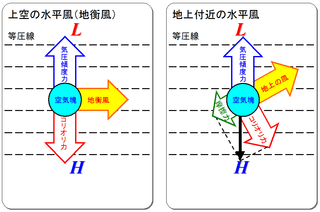
図2.上空の風と地上の風
図2には地上と上空の風の様子を示してみました。上空の大気については、x軸方向とy軸方向の運動方程式において、第一近似としてこれを定常流と見做すと、結局は気圧傾度力とコリオリの力の釣り合いに帰着するので、次の式で表されるような流れに書き直すことができます。
ug = -(1/fρ)(∂p/∂y)
vg = (1/fρ)(∂p/∂x)
このような上空の風を地衡風と呼びます。実は、上空の風はこの地衡風に近い状態で流れています。その一方で、地上の流れはさらに摩擦力が加わるため、風の向きが等圧線に対して傾いています。
続いて、今度は鉛直方向について考えてみましょう。図3のような気柱(大気の柱)を考えてみます。

図3.気柱と静力学平衡
柱の一部を赤い部分のような微小片として捉え、この微小片に働く力の釣り合いを考えましょう。重力は下向きに働き、これに抗して微小片を上向きに支える力は上下の気圧の差によって生じます。従って、重力と気圧の差による力の釣り合いは次のように表されます。
-ρ×S×Δz×g=Δp×S
これを簡単化して
Δp=-ρgΔz
この極限をとると、次のような静力学平衡の関係を得る事ができます。
(∂p/∂z)=-ρg
これは、鉛直スケールの運動が無視できると仮定した場合の鉛直方向の運動方程式であると言えます。
また、理想気体の状態方程式は次のように与えられます。
p=ρRT
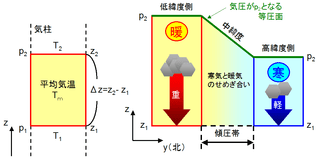
図4.層厚と傾圧帯
ここまでの知見を応用して、図4の左側に示すような気柱の中のz1~z2の部分の厚さΔzを求めてみましょう。この厚さは層厚(シックネス)と呼ばれ、上端と下端の気圧(p2、p1)と層内の平均気温Tmから次のように求める事ができます。
Δz=(RTm/g)ln(p1/p2)
気柱の底面における大気圧は気柱内に含まれる空気の総重量に比例しますが、この式の形から、この平均気温が高ければこの気柱の底面における気圧は高くなり、この平均気温が低ければこの気柱の底面における気圧は低くなると言えます。
図4の右側には北半球の様子を経線方向の断面図で模式的に表してみました。低緯度側では気温が高いため気柱の高さ(気圧がp2となる面=等圧面の高度)は高くなる一方、高緯度側では気温が低いため気柱の高さは低くなります。両者に挟まれた中緯度地方では、気柱の上端(気圧がp2の等圧面)は低緯度から高緯度に向かって傾斜しています。すなわち、低緯度から高緯度に向かって等圧面p2の坂道が作られていると考える事ができます。この等圧面の坂道の傾きを傾圧性と呼び、この傾きが緩やかであれば傾圧性が弱い、この傾きが急になるほど傾圧性が強いと言います。
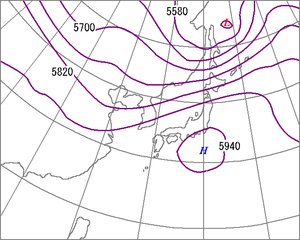
図5. 高層天気図で見る傾圧帯のイメージ図 (夏の場合)
図5には、500hPa面の高層天気図のイメージを示しました。地上天気図は海面上における気圧や前線の分布、そして地上の各種観測値を一つの地図上に重ねて表示していますが、上空の大気の様子を示す高層天気図は等圧面上の地図を描いています。この図は500hPa等圧面上の天気図であるため、この図面上はどこでも気圧が500hPaとなります。
この図の等値線は、気圧が500hPaとなる高度(ジオポテンシャル高度)を表しています。冬の天気予報で「上空5500m付近の寒気が・・・」と言うフレーズを良く聞くと思いますが、この「上空5500m付近」とは、500hPa等圧面の事を指しています。この高度では60m毎に等高度線が引いてあります。図5では、500hPa等圧面は日本の南海上では5940mと高くなる一方、オホーツク海上空で5520mと低くなっていますね。
この図の場合は、青森県からオホーツク海にかけては等圧面の坂道の傾きが急となるため傾圧性が強くなる一方、華中からシベリアにかけては等圧面の坂道の傾きが緩やかになるため傾圧性が弱い事が見て取れます。また、等高度線の形に注目してみると、沿海州から中国東北部、黄海を経て華中に向かって、下(南)に凸となる領域が広がっています。これが上空の気圧の谷(トラフ)です。その直ぐ西側では等高度線が上(北)に凸となる領域が広がっています。これが上空の気圧の峰(リッジ)です。
そういえば、ブログではここ2~3日、珍しく真面目に気象学の記事を書いているので(←本来はいつもそうあるべきなのですが)・・・ついでに?、大気の運動方程式についても触れておきましょう。
今回は、局地気象ではなく・・・むしろ局地気象に支配的な影響を及ぼす、北半球規模での大規模スケールの運動を考えてみましょう。図1のように北半球上に原点をとり、直交座標系を設定します。

図1.北半球上に設置された直交座標系
直交座標系内のある一部の空気の塊についての運動方程式は次のように表すことができます。
(x軸方向:東西方向) ρ(du/dt)=-(∂p/∂x)+ρfv+Fx
(y軸方向:南北方向) ρ(dv/dt)=-(∂p/∂y)+ρfu+Fy
(z軸方向:鉛直方向) ρ(dw/dt)=-(∂p/∂z) +Fz-ρg
ここで
(du/dt)=(∂/∂t)+u(∂/∂x)+v(∂/∂y)+w(∂/∂z)
f=2Ωsinφ
地球上の大気には、気圧傾度力、コリオリの力、摩擦力、重力の4つの力が働いています。コリオリの力とは、地球の自転に伴う慣性力で、進行方向の右向きに働きます。

図2.上空の風と地上の風
図2には地上と上空の風の様子を示してみました。上空の大気については、x軸方向とy軸方向の運動方程式において、第一近似としてこれを定常流と見做すと、結局は気圧傾度力とコリオリの力の釣り合いに帰着するので、次の式で表されるような流れに書き直すことができます。
ug = -(1/fρ)(∂p/∂y)
vg = (1/fρ)(∂p/∂x)
このような上空の風を地衡風と呼びます。実は、上空の風はこの地衡風に近い状態で流れています。その一方で、地上の流れはさらに摩擦力が加わるため、風の向きが等圧線に対して傾いています。
続いて、今度は鉛直方向について考えてみましょう。図3のような気柱(大気の柱)を考えてみます。

図3.気柱と静力学平衡
柱の一部を赤い部分のような微小片として捉え、この微小片に働く力の釣り合いを考えましょう。重力は下向きに働き、これに抗して微小片を上向きに支える力は上下の気圧の差によって生じます。従って、重力と気圧の差による力の釣り合いは次のように表されます。
-ρ×S×Δz×g=Δp×S
これを簡単化して
Δp=-ρgΔz
この極限をとると、次のような静力学平衡の関係を得る事ができます。
(∂p/∂z)=-ρg
これは、鉛直スケールの運動が無視できると仮定した場合の鉛直方向の運動方程式であると言えます。
また、理想気体の状態方程式は次のように与えられます。
p=ρRT

図4.層厚と傾圧帯
ここまでの知見を応用して、図4の左側に示すような気柱の中のz1~z2の部分の厚さΔzを求めてみましょう。この厚さは層厚(シックネス)と呼ばれ、上端と下端の気圧(p2、p1)と層内の平均気温Tmから次のように求める事ができます。
Δz=(RTm/g)ln(p1/p2)
気柱の底面における大気圧は気柱内に含まれる空気の総重量に比例しますが、この式の形から、この平均気温が高ければこの気柱の底面における気圧は高くなり、この平均気温が低ければこの気柱の底面における気圧は低くなると言えます。
図4の右側には北半球の様子を経線方向の断面図で模式的に表してみました。低緯度側では気温が高いため気柱の高さ(気圧がp2となる面=等圧面の高度)は高くなる一方、高緯度側では気温が低いため気柱の高さは低くなります。両者に挟まれた中緯度地方では、気柱の上端(気圧がp2の等圧面)は低緯度から高緯度に向かって傾斜しています。すなわち、低緯度から高緯度に向かって等圧面p2の坂道が作られていると考える事ができます。この等圧面の坂道の傾きを傾圧性と呼び、この傾きが緩やかであれば傾圧性が弱い、この傾きが急になるほど傾圧性が強いと言います。

図5. 高層天気図で見る傾圧帯のイメージ図 (夏の場合)
図5には、500hPa面の高層天気図のイメージを示しました。地上天気図は海面上における気圧や前線の分布、そして地上の各種観測値を一つの地図上に重ねて表示していますが、上空の大気の様子を示す高層天気図は等圧面上の地図を描いています。この図は500hPa等圧面上の天気図であるため、この図面上はどこでも気圧が500hPaとなります。
この図の等値線は、気圧が500hPaとなる高度(ジオポテンシャル高度)を表しています。冬の天気予報で「上空5500m付近の寒気が・・・」と言うフレーズを良く聞くと思いますが、この「上空5500m付近」とは、500hPa等圧面の事を指しています。この高度では60m毎に等高度線が引いてあります。図5では、500hPa等圧面は日本の南海上では5940mと高くなる一方、オホーツク海上空で5520mと低くなっていますね。
この図の場合は、青森県からオホーツク海にかけては等圧面の坂道の傾きが急となるため傾圧性が強くなる一方、華中からシベリアにかけては等圧面の坂道の傾きが緩やかになるため傾圧性が弱い事が見て取れます。また、等高度線の形に注目してみると、沿海州から中国東北部、黄海を経て華中に向かって、下(南)に凸となる領域が広がっています。これが上空の気圧の谷(トラフ)です。その直ぐ西側では等高度線が上(北)に凸となる領域が広がっています。これが上空の気圧の峰(リッジ)です。

















