先日の記事でも述べましたが、この夏の暑さは異常です。外に出るのも儘ならず、インドアで過ごすことが多くなりました。
そこで、この8月中はスキマ時間に「特殊相対性理論」の解説を読み返しておりました。工学部(機械系)で特殊相対性理論を履修したのは、約四半世紀前の大学1年(教養部)の頃です。使用された物理学の教科書では僅か「10ページ前後」の記述でしたが、なかなか難解でした。あらためて理解したイメージを「メモ書き」として記事に残しておきます。
【異なる2つの空間(K系とK'系)】
まずは一連の話の前提として、異なる2つの空間を導入します。一方の空間をK系、もう一方の空間をK'系と呼ぶことにしましょう。
K系は静止状態にあり、この中には観測者Aが存在します。また、K'系は一定の速度で動いており、この中には観測者Bが存在します。K系が駅のホームだとすると、K'系はホームを通過する新幹線のようなイメージです。

【慣性系】
ここで、K系とK'系のそれぞれに座標を設定します。これらの座標系は「慣性系」と呼ばれます。慣性系とは、慣性の法則が成立する座標系の事です。慣性の法則は「静止している物体は静止し続け、運動している物体は一定の速度を保ちながら運動を続ける」と言う法則です。
つまり、座標系は静止しているか等速運動をしているため、その加速度は常にゼロであり続けます。

【ガリレイ変換】
K'系内における点Pに着目し、この点Pの位置を観測者A、Bのそれぞれから見た場合の見え方について考えてみます。点Pの位置(座標は)は、観測者Aからはxの位置に見えます。そして、この位置xは時々刻々変化します。
一方、観測者Bからはx'の位置に静止しているように見えます。観測者Aの立場から言えば「観測者Bもまた点Pと共に同じ速度で動いている」のです。
この関係を等式で表し、時間微分を施すと、位置の関係から、速度や加速度が導かれます。その結果、運動方程式はK系、K'系で同じ形となります。

すなわち、一つの座標(慣性系)で成立する力学の原理は、これと等速運動する他の座標系(慣性系)についても成立します。従って、力学現象の基礎として絶対速度を測定する方法は無く、ただ相対速度のみが測定できる、と言うことです。これを「ガリレイの相対論」と言います。
【非慣性系と慣性力】
ここで、もしK'系が慣性系ではなかった場合を考えてみましょう。つまり、K'系が一定の「加速度」を持って運動している状況です。この場合、K'系は「非慣性系」と呼ばれます。

先ほどのガリレイ変換と同様に、K'系内における点Pに着目し、この点Pの位置を観測者A、Bのそれぞれからの見え方(位置)について式を立ててみます。時間微分を施すと、位置の関係から、速度や加速度が導かれます。

その結果、K'系の運動方程式の中に「-ma」と言う項(慣性力)が現れました。非慣性系の運動では、座標系自身の加速度に伴う「みかけの力」が新たに加わります。
【K'系における光の往復(1)】
ニュートンの運動方程式と慣性系の関係を概観した後は、マクスウェルの電磁方程式と慣性系の関係を見てみましょう。ここでは、運動する座標系(K'系)の中で光(電磁波)を往復させ、その様子を外部の静止系(K系)の観測者Aの目線で考察してみます。
まずはK'系の中で、光を(K'系の)進行方向に沿って、距離lだけ往復させてみます。

K'系では「光源から反射板までの光の速度はcであり、また反射板から反射される光の速度もcと認識される」と考えられます。
一方、K系では、K'系自体の速度vも加わるため、「光源から反射板までの光の(相対)速度はc+vであり、また反射板から反射される光の(相対)速度もc-vと認識される」と考えられます。
この結果、K系の観測者Aから見た場合の光の往復に要する時間t1が求められます。

【K'系における光の往復(2)】
続いて、K'系の中で、光を(K'系の)進行方向とは垂直に、距離lだけ往復させてみます。
K'系では「光源から反射板までの光の速度はcであり、また反射板から反射される光の速度もcと認識される」と考えられます。
一方、K系でも「光源から反射板までの光の速度はcであり、また反射板から反射される光の速度もcと認識される」と考えられます。
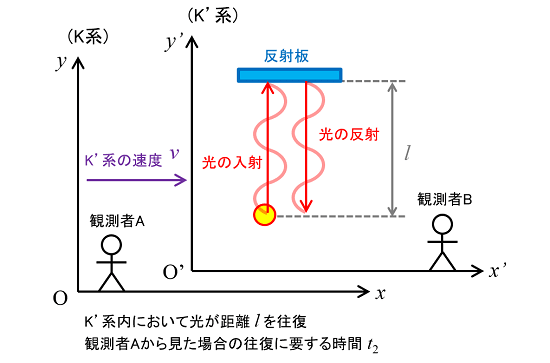
ただし、K'系自体の速度vの影響で、「光の進み方は『真っ直ぐ』ではなく『斜めに傾く』と認識される」と考えられます。
この結果、K系の観測者Aから見た場合の光の往復に要する時間t2が求められます。

【2種類の光を合わせると】
ここで、上記の2つの光(1)(2)を合わせた場合を考えてみます。
(1) K'系の進行方向に沿った方向(往復時間:t1)
(2) K'系の進行方向に垂直な方向(往復時間:t2)
当初、2つの光は時間差「Δt = t1 - t2」に相当する干渉を生じる(時間差がある=光路差がある)と考えられました。しかし、実際には観測されなかったのです(あれっ?)。
K系とK'系との間で「ニュートンの運動方程式」は変わらず適用できますが、「マクスウェルの電磁方程式」の場合はちょっと勝手が違うようです。そこで、次のような要請(アインシュタインの要請)が基本原理に組み込れました。
(1)1つの慣性系で成立する物理法則は、これと等速運動する他の座標系(慣性系)に対しても同じ形で成立する。
(2)真空中の光の速度は、光源および観測者の運動とは無関係に、常に一定である(光速不変の原理)。
つまり、光速が変化するのではなく、K'系の空間が歪む(縮む)ことで「Δt = t1 - t2 = 0」、つまり「t1 = t2」となる(←辻褄が合う)と考えます。この時、K'系の空間は元の長さlからl'に変化すると考えます。この結果、「t1 = t2」が実現すると考えると、次のような式が得られます。

このように、慣性系の速度に応じて内部の空間が縮むことを「ローレンツ収縮」と言います。
【ローレンツ変換】
ローレンツ収縮の概念を拡張してみます。
改めて、K系(静止)に光源を設置し、K'系(運動)の中にある点Pに向かって光を発射する状況を考えてみます。
ここで、K系とK'系の時刻をそれぞれt,t'と表すことにします。また、K系とK'系の座標をそれぞれx,x'と表すことにします。
初期状態(t = t' = 0)の時、K系とK'系は重なっており、この瞬間にK系の光源(x = 0)から光を発し、同時にK'系は速度vで動き出すものとします。
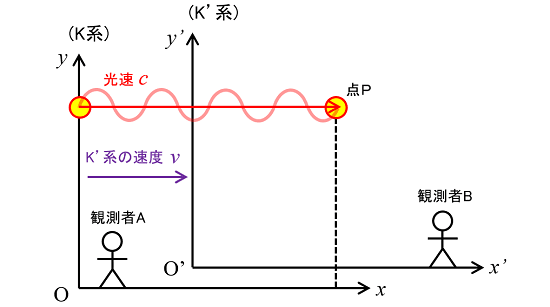
ある程度の時間(K系ではt、K'系ではt')が経過した後の様子を考えてみます。ここからは、座標系の取り方とは無関係に一様に流れる「絶対時間」という考え方を捨てて、各慣性系毎に異なる時間を考えます。
改めて、光の経路上に点P1、点P2、点P3を置いて考えてみます。P1~P2間はK系のみ、P2~P3間はK系とK'系が重なっている区間となります。

ここで、K系に固定された光源(点P1)から発せられた光は、点P2を経てK'系内に入り、点P3に到達したとします。
観測者Aの視点に立って、P1~P3間の距離を考えてみると、P1~P2間の距離は「時間tにおけるK'系の移動距離」であり、P2~P3間の距離は「K'系内を通過した距離」となります。
一方、観測者Bの視点に立って、P2~P3間の距離を考えると、やはり「K'系内を通過した距離」となります。
ここで、P2~P3間の距離について、2人の観測者の認識が異なります。観測者BはP2~P3間の距離をx'と認識しています。しかし、観測者Aはx'からローレンツ収縮した長さを認識しています。K'系内は空間そのものが収縮しているので、観測者Bも一緒に収縮していることになります。もちろん、観測者Bは自らの収縮を認識できません。
従って、観測者Aの認識をベースに、観測者Bが認識する空間x'と時間t'を表現すると、次のようになります。

つまり、K系とK'系では「空間の大きさが変わるのと同時に、時間の長さも変わる」ということです。この変換を「ローレンツ変換」と言います。また、この逆変換は次のようになります。

ここで、ローレンツ変換の式を基に、空間と時間の微小変化を考えてみましょう。
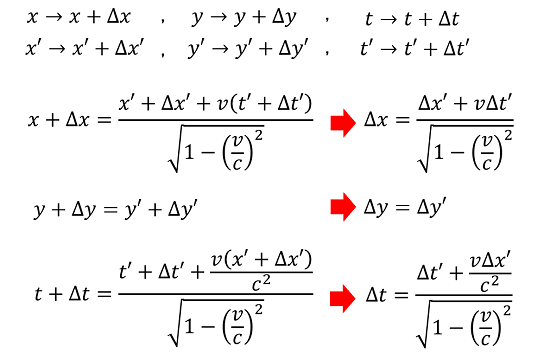
時間と空間の微小変化を基にして、速度成分のローレンツ変換の式を導くことができます。

この続きとなる「エネルギーと質量の等価性」は、こちらです。
ちなみに、現実の世界で身近な物理現象を考える際は、運動速度vは光速cよりも圧倒的に小さく「古典力学(ニュートン力学)」で十分対応できます。ローレンツ変換の式で「(v/c)→0」の極限を取ると、ガリレイ変換の式と一致します。
一方、「光速に近い速度で運動する、または天体のような巨大な質量を扱う」ような物理現象を扱う際には、この知識は必要になると学びました。今後の人生において、そのような現象を扱うことが「全く無い」とは言い切れないので、念のため勉強しておきます。
そこで、この8月中はスキマ時間に「特殊相対性理論」の解説を読み返しておりました。工学部(機械系)で特殊相対性理論を履修したのは、約四半世紀前の大学1年(教養部)の頃です。使用された物理学の教科書では僅か「10ページ前後」の記述でしたが、なかなか難解でした。あらためて理解したイメージを「メモ書き」として記事に残しておきます。
【異なる2つの空間(K系とK'系)】
まずは一連の話の前提として、異なる2つの空間を導入します。一方の空間をK系、もう一方の空間をK'系と呼ぶことにしましょう。
K系は静止状態にあり、この中には観測者Aが存在します。また、K'系は一定の速度で動いており、この中には観測者Bが存在します。K系が駅のホームだとすると、K'系はホームを通過する新幹線のようなイメージです。

【慣性系】
ここで、K系とK'系のそれぞれに座標を設定します。これらの座標系は「慣性系」と呼ばれます。慣性系とは、慣性の法則が成立する座標系の事です。慣性の法則は「静止している物体は静止し続け、運動している物体は一定の速度を保ちながら運動を続ける」と言う法則です。
つまり、座標系は静止しているか等速運動をしているため、その加速度は常にゼロであり続けます。

【ガリレイ変換】
K'系内における点Pに着目し、この点Pの位置を観測者A、Bのそれぞれから見た場合の見え方について考えてみます。点Pの位置(座標は)は、観測者Aからはxの位置に見えます。そして、この位置xは時々刻々変化します。
一方、観測者Bからはx'の位置に静止しているように見えます。観測者Aの立場から言えば「観測者Bもまた点Pと共に同じ速度で動いている」のです。
この関係を等式で表し、時間微分を施すと、位置の関係から、速度や加速度が導かれます。その結果、運動方程式はK系、K'系で同じ形となります。

すなわち、一つの座標(慣性系)で成立する力学の原理は、これと等速運動する他の座標系(慣性系)についても成立します。従って、力学現象の基礎として絶対速度を測定する方法は無く、ただ相対速度のみが測定できる、と言うことです。これを「ガリレイの相対論」と言います。
【非慣性系と慣性力】
ここで、もしK'系が慣性系ではなかった場合を考えてみましょう。つまり、K'系が一定の「加速度」を持って運動している状況です。この場合、K'系は「非慣性系」と呼ばれます。

先ほどのガリレイ変換と同様に、K'系内における点Pに着目し、この点Pの位置を観測者A、Bのそれぞれからの見え方(位置)について式を立ててみます。時間微分を施すと、位置の関係から、速度や加速度が導かれます。

その結果、K'系の運動方程式の中に「-ma」と言う項(慣性力)が現れました。非慣性系の運動では、座標系自身の加速度に伴う「みかけの力」が新たに加わります。
【K'系における光の往復(1)】
ニュートンの運動方程式と慣性系の関係を概観した後は、マクスウェルの電磁方程式と慣性系の関係を見てみましょう。ここでは、運動する座標系(K'系)の中で光(電磁波)を往復させ、その様子を外部の静止系(K系)の観測者Aの目線で考察してみます。
まずはK'系の中で、光を(K'系の)進行方向に沿って、距離lだけ往復させてみます。

K'系では「光源から反射板までの光の速度はcであり、また反射板から反射される光の速度もcと認識される」と考えられます。
一方、K系では、K'系自体の速度vも加わるため、「光源から反射板までの光の(相対)速度はc+vであり、また反射板から反射される光の(相対)速度もc-vと認識される」と考えられます。
この結果、K系の観測者Aから見た場合の光の往復に要する時間t1が求められます。

【K'系における光の往復(2)】
続いて、K'系の中で、光を(K'系の)進行方向とは垂直に、距離lだけ往復させてみます。
K'系では「光源から反射板までの光の速度はcであり、また反射板から反射される光の速度もcと認識される」と考えられます。
一方、K系でも「光源から反射板までの光の速度はcであり、また反射板から反射される光の速度もcと認識される」と考えられます。

ただし、K'系自体の速度vの影響で、「光の進み方は『真っ直ぐ』ではなく『斜めに傾く』と認識される」と考えられます。
この結果、K系の観測者Aから見た場合の光の往復に要する時間t2が求められます。

【2種類の光を合わせると】
ここで、上記の2つの光(1)(2)を合わせた場合を考えてみます。
(1) K'系の進行方向に沿った方向(往復時間:t1)
(2) K'系の進行方向に垂直な方向(往復時間:t2)
当初、2つの光は時間差「Δt = t1 - t2」に相当する干渉を生じる(時間差がある=光路差がある)と考えられました。しかし、実際には観測されなかったのです(あれっ?)。
K系とK'系との間で「ニュートンの運動方程式」は変わらず適用できますが、「マクスウェルの電磁方程式」の場合はちょっと勝手が違うようです。そこで、次のような要請(アインシュタインの要請)が基本原理に組み込れました。
(1)1つの慣性系で成立する物理法則は、これと等速運動する他の座標系(慣性系)に対しても同じ形で成立する。
(2)真空中の光の速度は、光源および観測者の運動とは無関係に、常に一定である(光速不変の原理)。
つまり、光速が変化するのではなく、K'系の空間が歪む(縮む)ことで「Δt = t1 - t2 = 0」、つまり「t1 = t2」となる(←辻褄が合う)と考えます。この時、K'系の空間は元の長さlからl'に変化すると考えます。この結果、「t1 = t2」が実現すると考えると、次のような式が得られます。

このように、慣性系の速度に応じて内部の空間が縮むことを「ローレンツ収縮」と言います。
【ローレンツ変換】
ローレンツ収縮の概念を拡張してみます。
改めて、K系(静止)に光源を設置し、K'系(運動)の中にある点Pに向かって光を発射する状況を考えてみます。
ここで、K系とK'系の時刻をそれぞれt,t'と表すことにします。また、K系とK'系の座標をそれぞれx,x'と表すことにします。
初期状態(t = t' = 0)の時、K系とK'系は重なっており、この瞬間にK系の光源(x = 0)から光を発し、同時にK'系は速度vで動き出すものとします。

ある程度の時間(K系ではt、K'系ではt')が経過した後の様子を考えてみます。ここからは、座標系の取り方とは無関係に一様に流れる「絶対時間」という考え方を捨てて、各慣性系毎に異なる時間を考えます。
改めて、光の経路上に点P1、点P2、点P3を置いて考えてみます。P1~P2間はK系のみ、P2~P3間はK系とK'系が重なっている区間となります。

ここで、K系に固定された光源(点P1)から発せられた光は、点P2を経てK'系内に入り、点P3に到達したとします。
観測者Aの視点に立って、P1~P3間の距離を考えてみると、P1~P2間の距離は「時間tにおけるK'系の移動距離」であり、P2~P3間の距離は「K'系内を通過した距離」となります。
一方、観測者Bの視点に立って、P2~P3間の距離を考えると、やはり「K'系内を通過した距離」となります。
ここで、P2~P3間の距離について、2人の観測者の認識が異なります。観測者BはP2~P3間の距離をx'と認識しています。しかし、観測者Aはx'からローレンツ収縮した長さを認識しています。K'系内は空間そのものが収縮しているので、観測者Bも一緒に収縮していることになります。もちろん、観測者Bは自らの収縮を認識できません。
従って、観測者Aの認識をベースに、観測者Bが認識する空間x'と時間t'を表現すると、次のようになります。

つまり、K系とK'系では「空間の大きさが変わるのと同時に、時間の長さも変わる」ということです。この変換を「ローレンツ変換」と言います。また、この逆変換は次のようになります。

ここで、ローレンツ変換の式を基に、空間と時間の微小変化を考えてみましょう。
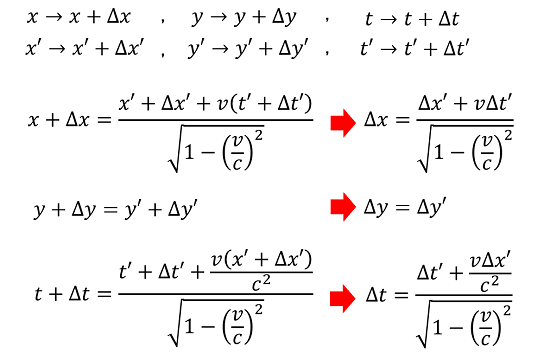
時間と空間の微小変化を基にして、速度成分のローレンツ変換の式を導くことができます。

この続きとなる「エネルギーと質量の等価性」は、こちらです。
ちなみに、現実の世界で身近な物理現象を考える際は、運動速度vは光速cよりも圧倒的に小さく「古典力学(ニュートン力学)」で十分対応できます。ローレンツ変換の式で「(v/c)→0」の極限を取ると、ガリレイ変換の式と一致します。
一方、「光速に近い速度で運動する、または天体のような巨大な質量を扱う」ような物理現象を扱う際には、この知識は必要になると学びました。今後の人生において、そのような現象を扱うことが「全く無い」とは言い切れないので、念のため勉強しておきます。

















