”四色問題”から眺めたウクライナ危機

　NHKBS｢笑わない数学｣(第3回)では､四色問題がテーマだ。
　｢四色定理｣とも呼ばれ､平面上のいかなる地図(領域)も”4色あれば同じ色が隣り合わずに塗り分けられる”という定理である。
　但し､(境界線ではなく)点のみを共有する領域は隣り合ってるとはみなされず､同色でもよい。

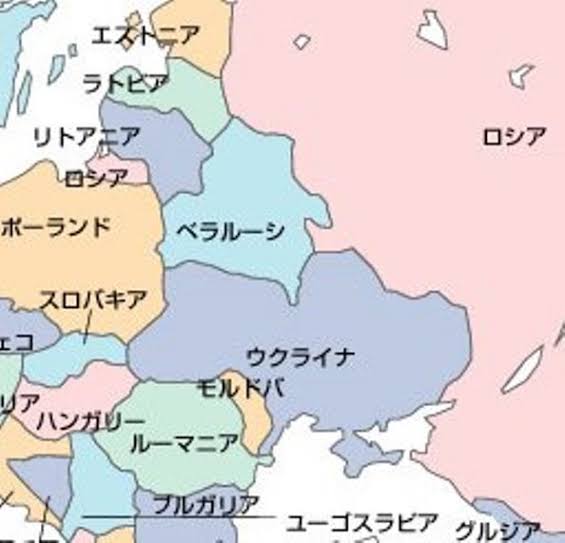
　この地図の”塗り分けの定理”を今回のウクライナ危機に例えてみる。
　そもそも､ウクライナをアメリカ(NATO)とロシアのニ色で塗り分けようとした時点で､大きな悲劇が待ち構えていた。
　中立を必死に訴えるウクライナだが､それだけでは三色になり､”塗り分けの定理”は成り立たず､長らく続いてきたウクライナ危機も一向に解決しない。
　つまり､ウクライナの悲劇を繰り返さない為には､ウクライナを囲む隣国の領域を(アメリカとロシアとEUの3つの色とは)異なった色で塗り直さなければならない。
　これを数学的に定義すればだが､”四色あれば十分”(=四色の定理)となる。
　故にウクライナの周りには､四色目となるアメリカ･ロシア･EUと､新たな中立圏が必要となり､これは私が｢結合則で見るウクライナ｣で提案した東欧圏である。

四色問題

　証明される前は四色問題と呼ばれ､1976年に一応は証明されたが､未証明の期間が長かった為､現在でも｢四色問題｣と呼ばれる事がある。
　(ウクライナと米と露の関係みたいに)3つの境界線が1点に集まる場所がある為､最低でも3色が必要である事は明らかですね。
　更に､ある領域の周囲に幾つかの領域がある場合､その領域が偶数(長野県は8個)であれば3色で塗り分けできるが､奇数個の領域で囲まれてる場合(ウクライナの場合は7個)は3色での塗り分けは(不可能で)4色が必要となる。
　そして､”4色あればどんな場合でも塗り分け可能なのか？”という事がこの｢四色問題｣の本質である。

　ここでは証明は(難解すぎて)省くが､この四食問題の歴史は偶然にも(ウクライナ危機の起源とされる)クリミア戦争の前の1852年に､フレデリック･ガスリー(英)により定式化され提案された。
　1890年になり､パーシー･ヒーウッド(英)により”地図を塗り分けるには5色で十分である”事が証明される(五色定理)。
　しかし､”4色で十分か？”という四食問題は､”平面グラフは4彩色可能である”という(離散数学の)グラフ理論における､最も有名な未解決問題として残った。
　1976年､ケネス･アッペル(米)とヴォルフガング･ハーケン(独)は､コンピュータを利用し約2000個(後に1405個)の”可約”な配置からなる”不可避集合”を見出し､何とか(力業で)四色定理を証明する？に至る。
　その後､アルゴリズムやプログラムの改良が行われ､不可避集合の数を1405個から633個に抑え､再証明が行われた。
　2004年､ジョルジュ･ゴンティエ(加)はよりシンプルな証明を行い､コンピュータ手法の洗練により､確かな手続きで証明が行われ､現在では四色問題は解決したとされる。

塗り分け可能なウクライナ問題

　四色定理の証明の手法は､以下の大きく2段階に分けられる。
　まずどんな平面グラフでも､その集合に属するグラフのどれか1つが部分グラフとして含まれる集合を考えた時､この様な性質を持つグラフの集合を”不可避集合”と呼ぶ。
　これは､かつてウクライナやベラルシが旧ソ連に含まれてた事を(不可避の現実として)イメージすれば判り易いですかね。
　因みに､ここで言う”グラフ理論”のグラフとは(関数のグラフではなく)､点(ノード)の集合に線や辺(エッジ)を書き加えたダイヤグラム(図式､構造)で表現される。
　例えば､路線図(ダイヤ)は(実際の地理の形状ではなく)駅と路線との”繋がり方”に注目する。この”点と繋がりを結ぶ線”の概念こそがグラフ(理論)である。

　次に､この不可避集合をうまく選ぶと､それに属するどのグラフも”可約”になる。
　つまり､その部分グラフを含むグラフがある時､その部分グラフを除いたものが4色で塗り分けが可能ならば､グラフ全体も4色で塗り分けができる。
　因みに､”可約”とは整数論や関数論でよく使われ､ある数やある多項式で割り切れる数や多項式を言います。一般的に言えば､ある単純なものに分解出来る。ここでは､ある領域(グラフ)が色分け出来る事を指します。
　これは､ウクライナが旧ソ連の(不可避な)領土だったとしても､上手く選べば”可約”になる。つまり､ウクライナがある独立した色に塗り分けられる事をイメージすれば､少しは理解しやすいですね。

　もっと冒険的に言えば(ですが)､例え戦争が不可避でも戦争そのものを4色で塗り分ける事は出来る。更に､4色に塗り分ける事で戦争を分散させる事は不可能じゃないとも言える。
　結局､どんな複雑な民族間の紛争も､たかが4色で塗り分けられると(少し強引すぎますが・・・)。

最後に〜四色問題が描くウクライナ

　前述のアッペルとハーケンはコンピュータによる実験を繰り返し､プログラムを何度も書き換え､可約なグラフから成る約2000個のグラフからなる不可避集合を求めた。当時のスパコンであるIBMSystem/370を､1200時間以上使用した､まさに力業とも言える証明でした。
　数学の世界では､複雑な問題に対し､簡潔にまとまった短い証明を”エレガントな解答”と言う事がある。四色定理に対する”力業による証明”は､これとは対極にあり､”エレファント(象)な証明”とも言われます。
　一方で､五色問題の証明は簡潔なもので､四色問題とは対照的でもあった。
　以上､ウィキを参考に主観を加え､簡単にまとめました。

　この様に､ウクライナ危機を数学的に記述する事で､ユニークな見方が出来ますね。
　ウクライナが中立ではなく四番目の色に染まる時､本当の意味での春が来るんでしょうか。
　いや､戦争や介入ではなく､四色問題の解法により平和が訪れてくれれば､数学フェチにとってはこれほど嬉しい事もない。