江戸時代に何故､数学が大ブームになったのか？〜和算とその時代”序盤”

　｢大河への道｣では､伊能図の完成に寄与した江戸時代の測量学や和算に少し触れました。特に測量学を支えたのが､江戸時代中期に栄えた和算でした。
　でも何故､江戸時代に数学(和算)が日本全国レヴェルで大ブームになったのか？
　そこで今日は､江戸時代の数学である”和算”について書きたいと思います。

”そろばん”伝来と江戸初期の和算

　結論から言えば､武士や農民や商人ら､年貢を集める側も収める側も､その年貢を計算する為にみんな数学が必要だった。更に､”そろばん”という便利な道具が現れた。
　江戸時代以前は､日常的な四則演算は､そろばんが伝来する前の計算道具である”算木”によって計算してた事が知られている。が､そろばんが日本に伝来し､日本の江戸時代の数学(和算)の歴史は始まったとされる。
　実は､そろばんは日本で発明されたものでなく､中国大陸のどこかで14世紀前後に発明され､それが瞬く間に中国大陸で普及し､日本にも伝来。1590年代に刊行された｢日葡辞書｣には"Soroban"という項目があり､計算道具としての記述がある。つまり､この頃には国内に流通し始めていた事が判る。
　以下､｢和算の歴史~第1章｣から大まかに纏めます。

　このそろばんは当時としては非常に簡便な計算道具で､以前の算木に比べると､手の上で弾き､迅速に計算できた。貿易の現場では重宝され､野外での測量や土木工事などでも威力を発揮した。江戸時代初期の屏風絵には､そろばんを弾いてる人物が描写されている。
　つまり､鎖国以前の日本における海外貿易関係者や土木工事や開墾にあたった人々の必需品こそがそろばんだったのだ。
　更に､この一世代程の間に､そろばんの知識は日本全国に広く浸透したとされる。
　この様に､江戸時代初期にそろばんが一気に普及すると､その入門書として｢塵劫記(じんこうき)｣が出版された。
　この背景には､商売や年貢の計算など､人々が数学を必要とする社会になった事も挙げられる。特に実用的側面で言えば､田畑の計算や毎年の暦を作る為の暦法計算､それに地図を作る為の測量術にて､数学(和算)が必要とされた。　

　更に､この入門書には仕事や実用に役立つだけでなく､好奇心をくすぐる楽しい問題も載っていて､庶民の中でも大ヒットし､数学ブームが起こる。
　因みに､｢塵劫記｣は京都の数学者･吉田光由が書いた数学書で､1627年に出版されると大人気となり､その後､改訂版が何度も出され､江戸時代を通して売れたロングセラーである。
　吉田の死後も｢塵劫記｣の類似本が数多く刊行され､江戸時代の日本人に初等的な算術の基礎を与えた。折しも､徳川幕府による治世は安定し､国内では農地開発を伴う土木事業が各地で盛んになった。こうした事業を監督する役人は､従来の様に槍や刀で武功を挙げて出世するでなく､民政を担当する事で頭角を現す新しいタイプの侍身分が期待された。各地でもそんな能力を持った人物が登用され､中には数学書を刊行する人々も現れる。

　しかし､｢塵劫記｣の教える四則演算は小学校の算数を集大成した内容で､その巻末に提示された遺題は､高校･大学初年級レベルの数学にも相当する難問だった。
　全く質的に異なる数学が必要となったが､当時の日本にはそれに対応する数学的技法はなかった。
　が､以下でも述べるが､幸運な事に｢算学啓蒙｣という13世紀末に中国で刊行された数学書がこの時代の日本に伝来していた。以下でも詳しく述べるが､その中に僅かに紹介されてた”天元術”が当時の多くの和算家の注目を集めた。
　この天元術とは､”算木”と呼ぶ小さな角棒を用いて､2次や3次方程式を立てるテクニックの事で､当時の数学の難問にはかなりの応用が利いたという。

　この天元術を日本風にアレンジし､更に応用の道を広げたのが当時､”算聖”と慕われた関孝和(?-1708)である。
　つまり､この偉人をきっかけに江戸の数学(和算)は大きく発展し､高度になっていく。
　以上､｢江戸の数学｣からでした。

 
和算探訪の旅

　和算とは､江戸時代から明治にかけて日本人が独自に研究･発展させた数学で､そのレベルは世界最高水準にあったとされる。
　例えば､関孝和の弟子である建部賢弘(1664-1739)は円周率πの計算で41桁まで弾き出し､関孝和の11桁を軽く上回った。更に､和算初の冪級数展開を考案し､これは天才レオンハルト･オイラーが微積分学を用いて同じ結果を発見する15年も前の事であった。
　建部賢弘の偉業は後で述べるとして､まずは”算聖”と崇められた関孝和からである。
　以下､｢江戸の科学者列伝｣から長々と抜粋します。

　ニュートン(1642-1727)とライプニッツ(1646-1716)と同世代である関孝和だが､彼ら微積分の創始者と並べられ紹介されてる事はあまり知られてはいない。
　和算とは江戸期の日本に独自に発達した数学で､記号を使って高度な代数や幾何を解くという点では洋算と変わらなかった。また､そのレベルも同時代の西洋数学と肩を並べるほどで､その立役者となったのが孝和である。
　孝和の研究でよく知られてるのが円周率の計算で､10万を超える角数の正多角形を使い､円周率を小数点以下11桁まで求めた。また連立方程式の解を求める公式をつくる過程で発見した行列式は､ヨーロッパに先駆ける発見だった。
　更に､n次方程式の近似的な解を求める方法の考案やベルヌーイ数の発見､円理(円弧に関する計算)の創始など､いずれも当時のヨーロッパの研究水準と遜色ないものだったとされる。
　幼くして大人の計算の誤りを指摘するなど､ガウスそっくりだが､早くから数理に目覚め､きっかけは前述の｢塵劫記｣(1627)を読んだ事だとされる。

　ここで和算の歴史を少し振り返ってみる。
　中国で発達した数学が日本に入ったのは飛鳥時代とされ､この時代はすでに官職として算博士が置かれ､実用数学と理論数学を研究し､また数学教育の任に当ったとの記録が残されてる。
　室町時代には中国からソロバンが伝来､これが改良されながら独自の発展を遂げ､戦国時代になると､武将たちの中に戦さや財政の必要から､数理に強い者を重用する傾向があらわれる様になった。
　それが和算として発展するのは江戸時代で､戦国の世が終わり､失職した武士の中にはソロバン塾で生計を立てる者も出た。藩士にも武より文が求められ､貨幣経済の発展と共に､経理に強い者が登用される様になる。
　この様な時代背景の元､ソロバンの教科書として数学入門書としてもよく読まれたのが｢塵劫記｣であったのだ。

和算の開祖･関孝和の偉業

　幼くして数学の面白さにとりつかれた孝和だが､師には就かず独学で学んでいく。つまり､師は書物であり､大きな影響を受けたのは､中国から伝わった数学書｢算学啓蒙｣(1299)と｢楊輝算法｣(1274-75)だ。が特に､朱世傑が著した｢算学啓蒙｣により最初に”天元術”に触れたとされる。
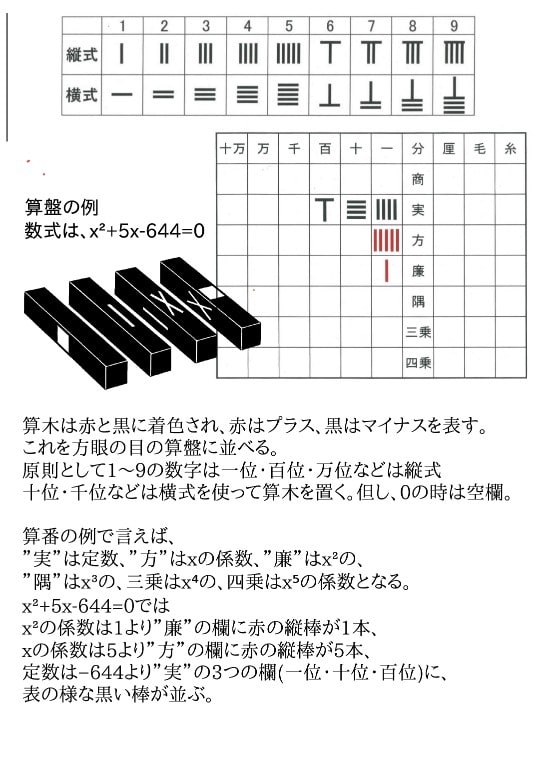
　因みに天元術とは､前述の算木(さんぎ)や算盤などの計算具を使う中国発祥の代数学の事で､算木には正数を表す赤い算木と負数を表す黒い算木の2種類がある。これを算盤と呼ぶマス目を書いた紙や布の上に並べ､その組合せで高次の代数方程式を解く事ができた(上図参照)。

　しかし､天元術には大きな制約があり､高次とても扱えるのは未知数が1つのみで､しかも係数が数字の数式(3x²+5x−22=0の様な)に限られた。この算木による方法の限界を悟った孝和は､一般の整式も表せる独自の方法を考案した。それは､算木の配列を紙に筆写し､式の係数に文字を付記する事だった。
　この表記法は”傍書法”と呼ばれ､等号やプラス記号こそなかったが､現代数学の記号法に通じるものだった。この”傍書法”に基づき開発されたのが”演段法”で､これは”配置”という補助数を使い､その後､補助数を消去し､文字係数の方程式をつくる方法だ。
　算木から記号への転換は､和算の発展にとって決定的だった。傍書法と演段法を合わせて､算木では不可能だった文字係数の高次多元方程式の計算が可能になったのだ。
　この記号的代数学の体系は後に､”点竄術”(てんざんじゅつ)と総称される。

　当時の代表的な和算家･沢口一之が著した｢古今算法記｣1671年)の巻末には､天元術では解けない15の遺題が載せられていた。これこそが各地の数学愛好者の挑戦意欲を刺激し､和算のレベルアップに貢献する事になる。
　こうして日本の数学は中国の数学から抜け出し､独自の数学―和算への道を歩み出したのだ。関はその成果を｢発微算法｣(1674)を著し､これは孝和が生前発刊した唯一の書であった。
　前述した様に､孝和の研究は多岐に渡るが､まずは円周率の計算がある。
　円周率を求める方法はアルキメデスの時代から知られ､円に内接する正多角形の角数を徐々に増やし､その辺の長さを計算し近似するというものだ。アルキメデスは正96角形を使って3.14という数字を得たが､孝和も同様な方法で正131072角形の辺の長さを計算し､円周率を小数以下11桁まで求め､更に､円周率を表す近似分数として355/113を示した。

　次に､ライプニッツに先駆けて導入したのが行列式の展開である。例えば､2×2行列を展開して計算する時､1行目がa,bで､2行目がc,dの正方行列の展開式はad－bcとなる。孝和はこれを2変数x,yを含む2つの連立方程式から､未知数を消去する過程でこの展開式を発見する。
　孝和は方程式を問題の性質により､解見題･解隠題･解伏題と分類し､解法を示した。解見題とは算術のみで解ける問題､解隠題とは未知数が1つの方程式､解伏題とは2つ以上の連立方程式を解く問題である。この解法の為に孝和が考案したのが上の行列式の展開である。
　因みに､行列式は西洋数学ではライプニッツが1693年に導入したのが最初とされるが､孝和の発見は約10年も前の事であった。後に孝和の解法は3次の行列式までは正しかったが､4次以上では誤りが判明する。

　更に､｢楊輝算法｣にヒントをえて､高次方程式の近似的な解を求める解法(ホーナー法)をも孝案する。ウィリアム･ホーナー(英)が同じ解法を発見したのは19世紀初めで､孝和は同等の解法を1世紀以上早く示してた事となる。
　また､”円理”の創建にも貢献。因みに､円理とは前出の円周率や円弧の研究から発展した和算の一分野で､孝和以降の発展によって三角関数や積分や無限級数などが扱われる様になった。
　また彼の死後に刊行された「概括算法｣(1712)には､ヤコブ･ベルヌーイ(仏)が発見したベルヌーイ数が示されている。両者ほぼ同時期の発見だった為､この級数は”関･ベルヌーイ数”とも呼ばれる。

　好奇心旺盛な孝和は､数学だけでなく天文学･暦学･測量学から機械仕掛け(からくり)などにも関心をもち､その才能を多方面で発揮する。暦学では改暦の研究が知られ､800年に渡って使われてきた宣明暦は誤差が大きくなり､使い物にならなくなっていた。これを改める為に第6代将軍徳川家宣は新しい暦の制定を孝和に命じる。
　家宣に仕え､江戸詰めとなり､勘定方吟味役にまで出世してた孝和だが､一大決心をし､中国の”授時暦”を参考に暦学を数学で基礎固めする。研究は大きな成果を挙げたが､その徹底さ故に作業自体の進行が遅れる。
　当時､孝和のライバルとされた幕府の碁打ちで､天文学者の渋川春海だが､西洋の暦法を採り入れ､誤差を修正し､暦をいち早く完成させた。暦は完全ではなかったが､諸大名を巧く味方につけ”貞享暦”として採用させる。
　一方､将軍の命を果たせなかった孝和の落胆は大きく､彼の数学研究をも衰退させたとされる。

 
関孝和の不運とその生涯

　建部賢弘らを筆頭に弟子には恵まれた孝和も､家族の縁には恵まれなかった。孝和の家族に関する資料は殆ど残されていないが､判る範囲では､遅くに結婚し､40代で2人の娘をもうけるも､不幸にも長女は幼少期に､次女は10代半ばで亡くなったという。
　跡継ぎがいない関家が養子として迎えたのが､弟永行の息子新七郎。関孝和の関する資料の散逸には､この新七郎の不行跡が関与していた。
　孝和の死により家督を相続した新七郎は甲府勤番士として赴任。赴任中､甲府城中の金庫から大金が盗まれる大事件が勃発。この事件の捜査で､新七郎が他の番士と博打をしてた事が露見。当然､重い処分を科せられ､関家は途絶えた。その際､孝和に関する資料も没収され､散逸してしまう。

　孝和の死後､彼が開拓した和算は弟子たちにより､更に高度な数学に発展し､江戸和算の全盛期が築かれた。しかしその和算も明治期に入ると洋算に代わられ衰退。それに伴い､孝和の業績も一部の研究者を除いて忘れられていく。
　かつては､日本には世界的数学者は存在しなかったというのが通説になっていた。理由は､公理から説き起こし､”抽象的な思考を進めるという思考スタイルが日本人には適さないからだ”とされてきた。一方､日本ではソロバンが発達し､計算に重きが置かれ､数学が理論的に発展しなかったという説もある。
　日本には関孝和も建部賢弘もいた。他にも沢山の優れた和算家を輩出した。江戸期には数学書がベストセラーになり､西洋と同じ記号による数学が隆盛を極める。日本人は決して数学が嫌いな訳でも数学的思考が苦手な訳でもなかったのだ。むしろ､庶民レベルでも大ブームとなった学問なのである。
　以上､｢大人の科学.net｣からでした。

　少し長くなりすぎたので､序盤はこれで終りにします。次回(中盤)は､実用数学としての和算と､その後について述べたいと思います。