小学生がたった1日で19×19までかんぺきに暗算できる本

11月30日発表の『第16回オリコン年間“本”ランキング2023』では、一般書籍部門にあたるBOOKランキングで小杉拓也氏の『小学生がたった1日で19×19までかんぺきに暗算できる本』が1位になり、話題となっている。

本作は東大卒でプロ算数講師である著者が、11×11～19×19を暗算できる「おみやげ算」の理論を紹介、演習までできる1冊だ。

子どもに教えられるよう作られているが、親世代やシニア世代が計算力や思考力を鍛えるため購入するという声も多い。

脳トレ本としてだけではなく、習得した計算法を孫に教えるコミュニケーションとしての需要もつかんでいたことが、ヒットにつながったと言える。

 

ここで言う「おみやげ算」とは、２桁同士の掛け算に使える計算方法の一種です。数字を移動させる動作が「お土産」に似ていることから名付けられた。

 

では実際に、「おみやげ算」の計算法について見てみよう。

Step①：片方の一の位を全てもう片方へ移す。

まず、かける数字の一の位を移し、キリのいい数に変えて計算しやすくする。

この問題の場合は、「15」から「5」を持ってきて、「14」に渡してあげます。
すると「（14＋5）×（15－5）」＝「19×10」となる。

キリのいい数にすれば、あとは掛け算する。
「1９×10＝1９0」

このように後ろの数字をキリのいい数にすることで、計算が楽になる。

一の位の数を移した結果、「20」や「30」になっても構いません。

Step②：一の位同士を掛け算する。

「14×15」の一の位同士を掛けるので、「4×5＝20」
これは簡単ですね。

Step③：求めた2つの数字を足す。

Step①で求めた「190」とStep②で求めた「20」を足す。
「190＋20＝210」
これが「14×15」の答えとなる。

 

図解で説明すると下記の通り。

 

 

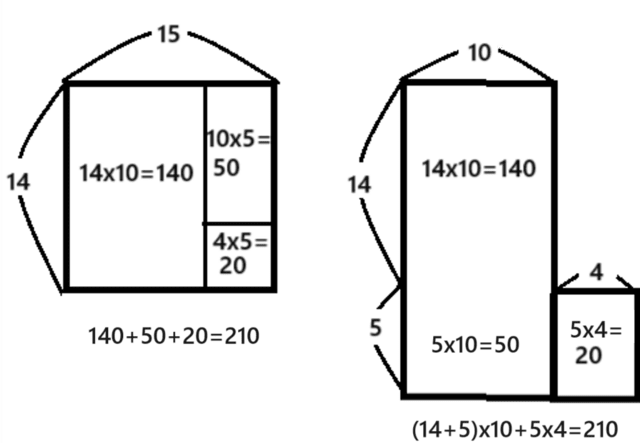
同様に、他の数字で計算してみよう。

87×84、45x45などでも、おみやげ算を使ってすべて計算できます。さっそく試してみましょう。

（例）87×84＝

①87×84の右の「84の一の位の4」をおみやげとして、左の87に渡します。すると、87×84が、（87＋4）×（84－4）＝91×80（＝7280）になります。

②その7280に、「87の一の位の7」と「おみやげの4」をかけた28をたした7308が答えです。
まとめると、87×84＝（87＋4）×（84－4）＋7×4＝7280＋28＝7308です

 

また、十の位が同じ数同士の応用例です。

165×14＝の例：

（1）分配法則によって、「165×14＝（160＋5）×14＝160×14＋5×14」と変形できます。

（2）「165×14＝160×14＋5×14」の、「160×14」は「16×14×10」と変形できるので、「16×14」を、おみやげ算を使って　　　解くと、次のようになります。

①16×14の右の「14の一の位の4」をおみやげとして、左の16に渡します。すると、16×14が、（16＋4）×（14－4）＝20×10（＝200）になります。

②その200に、「16の一の位の6」と「おみやげの4」をかけた24をたした224が、16×14の計算結果です。

これにより、「160×14＝16×14×10＝2240」と求められます。

（3）元の式に戻りましょう。「165×14＝160×14＋5×14」の、「160×14」は2240です。その2240に、（5×14＝）70をたすと、「2240＋70＝2310」となります。つまり、「165×14＝2310」ということです。

スムーズに暗算できたでしょうか。

 

しかし、残念ながら、おみやげ算は十の位が同じ数同士でしか使えない！

 

例えば、「28x15」をおみやげ算で計算できるのかを確かめてみよう。

1. 28+5＝33

2. 33✕10＝330

3. 8x5=40

4. 330+40=470

おみやげ算を使って暗算で計算すると、「28ｘ15=500」になります。

次に「28×15」を電卓で計算すると「28×15=420」となり、おみやげ算で計算する答えと異なることがわかりました。

以上のことから「28×15」はおみやげ算で計算できないことが判明した。

 

こちらの場合は、「2本曲線法」を覚えると、簡単に暗算ができるようになります。

手順は下記の通りです。

 2本曲線法がなぜ成り立つのか見てみよう。

ある2ケタの自然数の十の位をA、一の位をBとすると、その自然数は「10A＋B」と表せる。もう一方の2ケタの自然数の十の位をC、一の位をDとすると、その自然数は「10C＋D」と表せる。これをかけると：

「（10A＋B）×（10C＋D）＝100AC＋10AD＋10BC＋BD＝100AC＋10（AD＋BC）＋BD」　　となる。

一方、2本曲線法は、前述の説明から「100AC＋（AD＋BC）×10＋BD」と表せる。変形すると「100AC＋10（AD＋BC）＋BD」となる。2つの式は同じなので、2本曲線法が成り立つ。

 

脳の訓練になるだけでなく、大人にとっても目からウロコの計算法です。ぜひ親子または、お孫さんと一緒に楽しく学んでください。

 

 

ランキングに参加中。下記をクリックして応援お願いします！

にほんブログ村 

 

トップへ戻る（全体表示）