昨日の続きです。正規分布が役に立つ場面に「偏差値」があります。そう、あの試験の「偏差値」です。
偏差値は、私たちが中学生だった頃からいつの間にか馴染んでしまった言葉です。高校受験のとき、A高校は偏差値が60でちょっと難しい。偏差値55くらいのB高校を本命にして、滑り止めに50かそれ以下の高校も受けておこうか・・・なんて悩んだ人も多いことでしょう(数値はあくまでも参考です)。
「偏差値って、要は成績の順番を表す数字でしょ?」と言われるかもしれません。まあ、実際そうなんですが・・・。では、例を挙げて実際に偏差値を計算してみましょう。電卓のご用意を。
あるクラス(10人)が英語と数学のテストを受けました。その結果が以下の表です。

合計点では小林君が1位、佐藤さんが2位です。二人とも得意科目で90点を取っています。では、どちらの90点の方がより「価値」があるでしょうか?
それを判断するために、平均点(数学は60点、英語は70点)からどれだけ上回っているかを計算します。つまり、点数-平均点を出せばよいわけです。
小林君の得意な数学は90-60=30点の差、佐藤さんの得意な英語は90-70=20点の差を勝ちとっています。
この、点数-平均点を偏差と言います。全員分の偏差を出したものが以下の表です。偏差は、平均点との差ですから、平均点より少なければマイナスになります。したがって、全部を合計すればゼロになります。
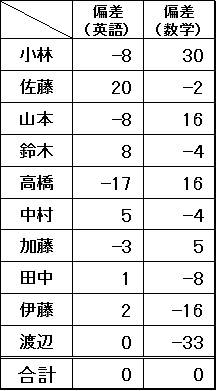
ここで偏差値の「偏差」が明らかになったわけです。
次は、クラス全体の英語と数学、それぞれの点数のバラツキ(散らばり具合)を数字で示します。
なぜ、そんなことをするのでしょう。
皆の点数が平均点近くに集まっているとき、ある人の偏差がかなり大きければ(それだけ皆の点数から離れていますから)「価値がある」と言えます。
一方、平均点から離れている人がちらほらいたとすれば、そこまで価値があるとは言えないでしょう。
ちょっと長くなりましたので、ここから先はまた明日ということで・・・。
(人材育成社)










