(引用つづき)『数学の流れ30講(中)』(志賀浩二著)
実際
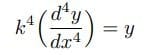
の解としては、この微分方程式の特性方程式(d/dxをpでおきかえたもの)

の根
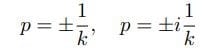
に対して、
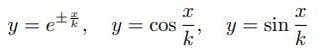
が出てくる。
これから、オイラーの天才の閃きの中で、驚くべき関係

がはじめて見出された。これは
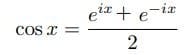 (1)
(1)
とかいても同じことである。これからすぐに

も導かれる。オイラーの公式は微分方程式から生まれてきたのである。
(引用おわり)
余弦の公式(1)からすぐに正弦の関係が導かれたという(たしかに微分すれば一瞬である)が、3年ほどかかったのではないかというのが、私が提起している公式の経緯である。また、公式は指数関数と三角関数の関係というより、虚数が実数の弧と関係していることにはじめは着目されていたのではないかと考えている(「オイラーの公式――起承転結」や12月の記事「オイラーの公式を近くで見る」で展開している)。
1741年と1742年のゴールドバッハへの手紙の式は特殊な形で、公式(1)に到達していない。1739年のベルヌーイ宛の手紙に公式(1)がかいてあるとも思えない。実際のところ、どうだったのだろうか。
実際
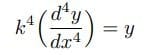
の解としては、この微分方程式の特性方程式(d/dxをpでおきかえたもの)

の根
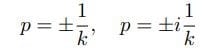
に対して、
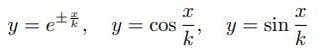
が出てくる。
これから、オイラーの天才の閃きの中で、驚くべき関係

がはじめて見出された。これは
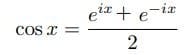 (1)
(1)とかいても同じことである。これからすぐに

も導かれる。オイラーの公式は微分方程式から生まれてきたのである。
(引用おわり)
余弦の公式(1)からすぐに正弦の関係が導かれたという(たしかに微分すれば一瞬である)が、3年ほどかかったのではないかというのが、私が提起している公式の経緯である。また、公式は指数関数と三角関数の関係というより、虚数が実数の弧と関係していることにはじめは着目されていたのではないかと考えている(「オイラーの公式――起承転結」や12月の記事「オイラーの公式を近くで見る」で展開している)。
1741年と1742年のゴールドバッハへの手紙の式は特殊な形で、公式(1)に到達していない。1739年のベルヌーイ宛の手紙に公式(1)がかいてあるとも思えない。実際のところ、どうだったのだろうか。










 (1741年)
(1741年) (1742年)
(1742年)







