ケプラーの『新天文学』第56章の「目覚め」をあきらかにするために、単純な図を提示してみよう。
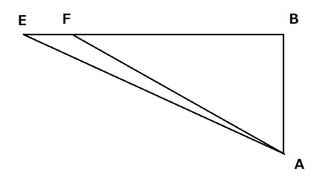
これはケプラーの楕円軌道発見の図の中心部分を取り出したものである。山本義隆と比較するために、記号は変えてある。Eは離心円上の点、Fは楕円上の点(観測結果が示す点)、Bは離心円の中心、Aは太陽である。山本義隆の楕円軌道発見図では、太陽Aと離心円上の点Eを結ぶ線はなく、∠BFAが5°18′と考えられている。この図ではAEは結ばれていて、∠BEAを5°18′と考えている。この2つの点で、これは山本義隆の発見図に対するアンチテーゼである。
エイトンは「目覚め」を次のように述べた。
「太陽から惑星への距離FAはEB、すなわち離心円の直径へのEAの投影に等しい」
FA=EA・cos(∠BEA)=EB
どのようにこの考えにケプラーが至ったのかといえば、ぼうだいな数の数値の中から、特別な数値が目に留まったからである。
上の図の線分はすべて長さが決まっている。それを取り出してみよう。
離心円の半径EBは1、離心距離BAは0.09265、切り取る三日月の幅EFは0.00429である。これをもとに、直角三角形に着目し三平方の定理を使って、FA、EAを求めることができる。
直角三角形FBAに着目して、FA
2=(1-0.00429)
2+0.09265
2より、FA=1.00001≒1。
直角三角形EBAに着目して、EA
2=1
2+0.09265
2より、EA=1.00428≒1.00429。
まとめると、FA=1、EA=1.00429である。そして、EB=1である。
ケプラーは次のように述べていた。(ここから半径は1ではなく100000である。)
(引用はじめ)
全く偶然に最大の視覚的均差を測り取った5°18´という角度の正割に思い至った。この値が100429であることを見たとき、まるで新たな光のもと、眠りから目覚めたかのように、以下の推論をし始めた。平均的な長さを取る所で均差の視覚的部分が最大になる。平均的な長さを取る所で三日月形つまり距離の短縮分が最大になり、ちょうど最大の視覚的均差の正割100429 が半径100000 を上回る分になる。したがって、平均的な長さを取る所で正割の代りに半径を用いると観測結果のとおりとなる。
(引用おわり)
正割は余弦の逆数である。EB・sec(∠BEA)=EAである。この関係を数値で表せば、100000sec(5°18′)=100429となる。正割と半径(底辺)は100429と100000である。その差は429である。また半径100000は観測結果(太陽と惑星への距離)100000と同じである。「最大の視覚的均差を測り取った5°18´という角度の正割」の値100429が、EAとEBとFAをつなぎ合わせて、「目覚め」を支えている。まずEA=EB・sec(5°18′)、次にFA=EB。そしてFA=EA・cos(∠BEA)=EBだったろう。
ケプラーは「正割EA(100429)の代りに半径EB(100000)を用いると観測結果FA(100000)のとおりとなる」と推論する。これが求めていた方法である。これで離心円から三日月形を切り取った軌道(楕円)になるだろう。半径(直径距離)を媒介にすればよい。

「正割の代りに半径を用いると観測結果のとおりとなる」は、「円軌道を放棄すると同時に、その円形性からの外れ」(山本義隆の表現)の端的な表現である。「正割」EAはプトレマイオスである。「観測結果」FAはティコ・ブラエである。そして、「半径」EBはケプラーである。ケプラーは半径(直径距離)を媒介にして、「離心円から三日月形を切り取った軌道(楕円)」を展望する。円周距離EAの代わりに、直径距離EBを用いると、求めていた軌道が得られる。「円から楕円へ」の歩みが、『新天文学』第56章で始まったのである。
山本義隆の楕円軌道発見の説明や図には「正割の代わりに」が欠如している。エイトンの3段階の「直径距離の法則」に対して、山本の「直径距離の法則」は2段階である。そこには、ティコ・ブラエとケプラーだけがいて、プトレマイオスは見当たらないのである。それでは「直径距離」の媒介性が明確にならない。正割EAは盲点になっているのである。
EとAが結ばれていないから∠BFAを5°18′と考えたのか、∠BFAを5°18′と考えたからEとAを結ばなかったのかはよくわからない。いずれにせよ、「正割の代わり」が欠けていることは、離心円上に端点をもつ「正割」(EA)を離心円から切り離し(FA)、離心円上に頂点をもつ5°18′(∠BEA) を離心円から切り離す(∠BFA)ことになった。
△BEAではなく、△BFAに注意がそそがれ、次のような誤った「目覚め」が演出されたのである。
FA=
FBsec(5°18′)=(1-0.00429) (1+0.00429)a≒a=
EB
(つづく)

















