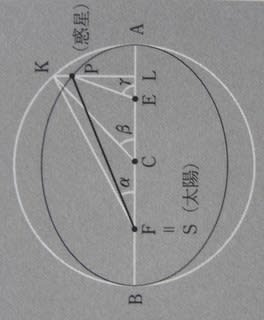
『新天文学』56章にでてくる100429(基準が100000、基準が1のときは1.00429)は、
離心円上にある火星と太陽の間の距離
rの、離心率
eの2次までの近似式
r=
a(1+
ecos
β+
e2/2・sin
2β)
において、
β=90°のとき、火星の離心率e=0.09265(ケプラーの値)を代入したものである。
すなわち、(1+
e2/2)=1.00429
である。(「100429の数学的背景」、「離心円に内在する楕円1」参照)
この指摘は単純で、これまでだれか指摘しているかもしれないが、見たことはない。わたしの「気づき」であり、おおげさにいえば「発見」である。山本義隆は離心円上にある惑星と太陽の間の距離
rの近似式について述べている。しかし、これと1.00429の関係についてはふれていない。関心がないのである。それは「ケプラーの第1法則(楕円軌道)の発見」の図12.11(『世界の見方の転換』3)において、AとEは結ばれておらず、離心円上にある火星と太陽の間の距離
rが視野に入っていないことからわかる。(「楕円軌道の発見」5,6参照)

山本義隆が指摘しているのは三日月の幅
EFが0.00429であり、この値は
e2/2に等しいことである。
(引用はじめ)
したがって正しい軌道の円(
b=a)と近似楕円(
b=(1-
e2)
a)の中間、すなわち
b=(1-
e2/2)
aとなる楕円であろうと考えられる。つまり、すでに求めていた火星の離心率
e=0.09265に対して、円から切り取るべき三日月の幅
a-bは、卵型を近似した上記の楕円の場合では
e2a=0.00858
aとなったが、正しくはその半分
e2a/2=0.00429
aでなければならない。(半径
aを1として読んでください。引用者注)
(引用おわり)
ここで
e2/2は、楕円の短半径を離心率
eの2次までとった近似式にでてくるものである。
長半径を1とした場合、短半径は
√(1-
e2)=(1-
e2)
1/2=1-
e2/2となる(注)。
すなわち、長半径と短半径の差は
1-(1-
e2/2)=
e2/2
となる。
この2つの出自の違う
e2/2によって、ケプラーの「目覚め」に接近できる。目覚めは次のようだった。
(引用はじめ)
全く偶然に最大の視覚的均差を測り取った5°18´という角度の正割に思い至った。この値が100429であることを見たとき、まるで新たな光のもと、眠りから目覚めたかのように、以下の推論をし始めた。平均的な長さを取る所で均差の視覚的部分が最大になる。平均的な長さを取る所で三日月形つまり距離の短縮分が最大になり、ちょうど最大の視覚的均差の正割100429が半径100000を上回る分になる。したがって、平均的な長さを取る所で正割の代りに半径を用いると観測結果のとおりとなる。
(引用おわり)
ケプラーは三日月の最大の幅429を切り取る理由と方法を考えていた。偶然、5°18´という角度の正割の値が100429であることを知る。429は、最大の視覚的均差の正割100429が半径100000を上回る分である。429は離心円と楕円を結びつけている。ケプラーの「目覚め」を次のようにいうことができる。
正割と半径(離心円の半径)の差を、e2までの近似で表した式と値
(1+e2/2)-1=e2/2=0.00429
と
楕円の長半径(離心円の半径)と短半径の差(三日月の幅)を、e2までの近似で表した式と値
1-(1-e2/2) =e2/2=0.00429
が結びついたのである。
これが「目覚め」の数学的背景である。離心円は切り取られ楕円になる。離心円の離心点と等化点(エカント点)は、そのまま楕円の2つの焦点となる。
e2/2が媒介したのである。
(注)
2次までの近似式について。
f(
e)=√(1-
e2)=(1-
e2)
1/2とする。
f'(
e)
=1/2・(1-
e2)
-1/2 ・(-2
e)
=-
e (1-
e2)
-1/2
f"(
e)〔は積の微分とみて〕
=-(1-
e2)
-1/2+(-
e)(-1/2・(1-
e2)
-3/2 ・(-2
e))
=-(1-
e2)
-1/2+
e2 (1-
e2)
-3/2
したがって、
e=0を代入すると、
f(0)=1
f'(0)=0
f"(0)=-1
ゆえに、
f(e)=
f(0)+
f'(0)e+
f"(0)
e2/2!
=1-
e2/2