ネイピアの対数の考えを説明する図が、『数の大航海』でも『数学の流れ30講 中』でも同じように、107とあるべきところが、10-7となっている(2か所)と述べ、校正の不備を指摘した。
ところが、『中高一貫数学コース 数学3をたのしむ』では正しく107となっていた。
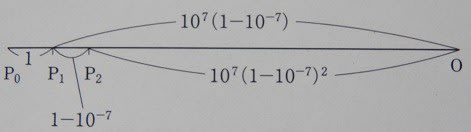
しかも、前2書の本文の説明で、不親切と思われた展開も、志賀先生らしく配慮が届いていた。
P1P2~10-7×107(1-10-7)=1-10-7を示した後、
前2書では、
P2O~107(1-10-7)-(1-10-7)=107(1-10-7)2
となっているだけだったが、
後書では、
P2O~107(1-10-7)-(1-10-7)
=107(1-10-7)-10710-7(1-10-7)
=107(1-10-7)2
となっていたのである。
『数の大航海』(1999年、日本評論社)
『数学の流れ30講 中』(2007年、朝倉書店)
『中高一貫数学コース 数学3をたのしむ』(2003年、岩波書店)
岩波書店の校正に軍配が上がる。
ところが、『中高一貫数学コース 数学3をたのしむ』では正しく107となっていた。
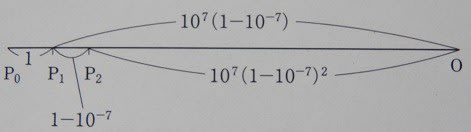
しかも、前2書の本文の説明で、不親切と思われた展開も、志賀先生らしく配慮が届いていた。
P1P2~10-7×107(1-10-7)=1-10-7を示した後、
前2書では、
P2O~107(1-10-7)-(1-10-7)=107(1-10-7)2
となっているだけだったが、
後書では、
P2O~107(1-10-7)-(1-10-7)
=107(1-10-7)-10710-7(1-10-7)
=107(1-10-7)2
となっていたのである。
『数の大航海』(1999年、日本評論社)
『数学の流れ30講 中』(2007年、朝倉書店)
『中高一貫数学コース 数学3をたのしむ』(2003年、岩波書店)
岩波書店の校正に軍配が上がる。










 1741年
1741年 1742年
1742年


