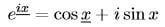点Zについて

ケプラーは、火星の位置Mを見いだす直前に、火星の位置として点Zを想定している。これまでふれてこなかったが、取り上げるとしよう。
まず、山本義隆を確認しておこう。（『世界の見方の転換』3）
（引用はじめ）

したがって、残された問題は、火星までの距離がこのように（直径距離として、引用者注）与えられたときの火星の正しい方向、つまり真アノーマリーαを見いだすことにあった。ケプラーは、第58章で、その目的を「距離を観測結果に一致させるだけではなく、角度をも同様に正しく与えるような物理的仮説を見いだすこと」としている。物理的な考察からすると、磁力による変動は当然直径にそってであろうと考えられたので、はじめにケプラーは、図12.11で太陽Aから距離r＝a(1＋ecosβ)にある惑星の位置を半径BK上の点Zと想定した。しかし、その場合には真アノーマリーに無視しえない5.5分の食い違いが生じた。そこで、そのすぐ近くの点である、Kから長軸線HIにおろした垂線KL上で太陽Aからの距離がr＝a(1＋ecosβ)となる点を火星の位置Mととれば、正しい角度を与えることを見いだした。
（引用おわり）
点Zを捨て点Mを選んだ理由について見ていきたいと思う。

ゆきとしろはら

先週の金曜日、2日続きの雪景色だった。朝、モズが訪れたが、昼からはシロハラが庭を歩いていた。

足元にジャノヒゲの青い実が一粒写っている。雪は溶けてしまったが、寒い日が続いている。

数式の比較 HTMLとLaTex

HTMLで数式を書くことはできる。指数（上付き文字）x²や添え字（下付き文字）a_nは問題ないだろうが、分数や平方根になると苦しくなり、シグマやインテグラルや極限などはほぼ無理になる。
数式はLatexが一番である。しかし、準備が大変で、あまり使わないので、新しいパソコンにはインストールしないことにした。その代わり、Webサイト（Cloud LaTex）を利用することにした。数式だけをピンポイントに利用するつもりである。PDFに表した数式を画像jpegとして取り出しブログに張り付ける。
複素数（２元数）と４元数のオイラーの公式を比較してみよう。
HTML
e^ix＝cos x + i sin x
e^ix+jy+kz＝cos √(x²+y²+z²) + (ix+jy+kz)/√(x²+y²+z²)･sin √(x²+y²+z²)
ここでは標準よりもフォントを大きくしている。
Latexでは次のようになる。


こちらが見やすいが、この辺まではHTMLでも許されるだろう。

モズあらわれる

今朝も雪が積もっていたが、風はほとんどなく、落ち着いた雪景色であった。何音節もある鋭い鳥の鳴き声がした。記憶になかった。玄関を開けると、南天に止まっていた鳥が飛び立っていった。鳥は電柱のてっぺんのワイヤーに止まってしばらく動かなかった。
　
名前が浮かばない。腹はジョウビタキにみえるが、頭部が違う。知らない鳥だと思った。目の近くの黒い帯が目印になるだろうか。
どうやらモズ（百舌、百舌鳥、鵙）のようである。名前は聞いたことがある。こんどは庭に降りてきたところを撮ってみたい。2日続きの雪景色に迷ったのだろうか。大歓迎である。

ふきとゆき

昨日の午後3時ごろから雪が降り始めた。みるみる積もっていった。今季、３度目の雪である。
今朝は、妻も子供も職場の雪かきのため早めに出かけた。寒く、風も強いが、日差しはあった。窓から見ていると、ビワやナンテンやユスラウメに積もっていた雪は徐々になくなっていった。庭も一面の白色から午後には土色が見えはじめた。雪靴をはいて庭に出る。ふきのとうは年が明けたころから出はじめていた。咲きはじめる春と溶けてゆく冬。

三日月の幅4

一般的な三日月の幅KMを求めよう。離心円の半径を1、離心率をeとする。

KM＝KL－MLである。
KLは△KLBに着目して、KL＝sinβ。
MLは△MLAに着目する。
ML²＝MA²－AL²
ここで、ケプラーの方法を確認しておこう。β＝90度のとき、直角三角形EBAに着目した。
火星と太陽の距離FAとして、正割EAではなく半径EB（＝1）を用いることによって、FA＝1とした。
K点では直角三角形KTAに着目することになる。火星と太陽の距離MAとして、正割KAではなく半径（直径距離）KTを用いる。MA＝KTである。

KT＝KB＋BT
＝1＋ecosβ
また、AL＝AB＋BL
＝e＋cosβ
である。
したがって、
ML²＝MA²－AL²
＝KT²－AL²
＝(1＋ecosβ)²－(e＋cosβ)²
＝(1－e²)(1－cosβ²）
＝(1－e²)sinβ²
したがって、ML＝√(1－e²)sinβ
したがって、一般的な三日月の幅KMは、
KM＝KL－ML
＝sinβ－√(1－e²)sinβ
＝sinβ(1－√(1－e²))
これが一般的な三日月の幅の式になる。また、KL:ML＝1: √(1－e²)である。

離心アノマリアβが0°から180°へと大きくなるにつれて、離心円から一定の割合で三日月が切り取られ、90°で最大の幅1－√(1－e²)を切り取って、楕円軌道が描かれていく過程をたどることができる。

三日月の幅3

離心円の半径を1、離心率をeとする。

図で、EB＝1、BA＝eである。火星と太陽の距離として、正割EAではなく半径EBを用いることによって、FA＝1である。FB＝√(1－e²）となり、三日月の幅EFは、
EF＝1－√(1－e²）
となる。
ここで、√(1－e²）の近似式を考える。e²まで（e²の1次までの）の近似（注）で、
√（1－e²）＝1－1/2･e²
したがって、
EF
＝1－(1－1/2･e²）
＝1/2･e²
ここにe＝0.09265を代入すると、
EF
＝0.00429となり、
切り取られるべき三日月の幅と実際に切り取られた幅の値に違いはない。

しかし、e⁴まで（e²の2次まで）の近似（注）を考えると、
√(1－e²）＝1－1/2・e²－1/8･e⁴
したがって、
EF
＝1－(1－1/2・e²－1/8･e⁴）
＝1/2・e²＋1/8･e⁴
ここにe＝0.09265を代入すると、
EF
＝0.00429＋0.00001
＝0.00430
となり、
切り取られるべき三日月の幅と実際に切り取られた幅の値に違いが生じていたことがわかる。

次に、一般的な三日月の幅についてみておこう。

（注）
（1＋x)ⁿ＝1＋nx＋1/2･n(n－1)x²＋…
において、n＝1/2、x＝－e²とおく。

うぐいすいろ

鶯色（うぐいすいろ）は、抹茶の色に近い柔らかな黄緑色ではなく、灰色がかった緑褐色だという。灰色がかった緑褐色はウグイスの羽の色を再現したもので、正式な鶯色である。これに対して、柔らかな黄緑色の方はメジロをウグイスと混同したもので、鶯色ではなく、「鶯をイメージした色」のようである。写真で確認してみよう。

ビワのつぼみやメジロの腹部の褐色の部分が「鶯色」で、メジロの羽や頭部の黄緑色は「鶯をイメージした色」である。

三日月の幅2

図（注1）で数値を確認しておこう。

離心円の半径は１である。三日月の幅EFは0.00429、離心距離BAは0.09265である。これらはティコ・ブラーエのデータである。これをもとに、火星と太陽の距離FAは、△FABに着目することによって求めることができる。
FA²=FB²＋AB²
＝(1－0.00429)²＋0.09265²
＝1.00002
したがって、
FA=1.00001

ケプラーは「平均的な長さを取る所で正割の代りに半径を用いると観測結果のとおりとなる」と述べている。平均的な長さを取る所とは、離心円上の点E。また、正割（注2）はEAであり、半径はEBである（直角三角形EBAに着目）。ケプラーが気づいたのは、火星はEではなくFにあり、火星－太陽間の距離として、正割EA（＝1.00429）ではなく半径EB（＝1）を用いれば、観測結果（FA＝1.00001）の通りになることである。たしかに1.00001≒1である。

FAの距離は、EA＝1.00429ではなく、EB=1。これがケプラーの洞察である。ティコの観測値はFA=1.00001だが、これを正確に半径の値1、強調していえば、1.00000と置く。この場合、ティコのデータに依存せず、FA=1.00000となる。観測値の1.00001の近似値ではなく、理論値の1.00000である。

楕円軌道が発見されるまでは、直角三角形FBAにおいて、未定なのはFAで、FB＝1－0.00429、BA＝0.09265はわかっていた。FAはデータから計算するものだった。しかし、楕円軌道の端緒が発見されたとき、未定なのはFBで、FA＝1.00000、BA＝0.09265はわかっている。こんどはFA＝1.00000が起点となる。FBを求めてみよう。

直角三角形FBAで、FA=1、BA=0.09265である。
三平方の定理より、
FB²=1²－0.09265²
＝1－0.008584
＝0.991416
したがって、
FB
＝√0.991416
＝0.99570

したがって、三日月の幅の値EFは、
EF＝1－0.99570
＝0.00430

切り取られるべき三日月の幅は0.00429だったが、実際に切り取られた幅の値は0.00430である。
わずかだが、違いはあったというべきだろう。
0.00001の差とは、100メートルに対して1ミリの差である。違いはあるが、同じというべきだろうか。

数値を使って三日月の幅を見てきたが、こんどは離心率eのまま、三日月の幅を検討してみよう。

（注1）
この図は、『世界の見方の転換』3で提示されている図「ケプラーの第1法則（楕円軌道）の発見」に離心円上の点E、Kと太陽Aを結んだ線分を付け加えたものである。（「楕円軌道の発見」5,6など参照）
（注2）
「正割」の値はティコのデータとは無関係である。正割は余弦の逆数である。ケプラーは∠BEAが5°18´である△BEAに着目していた。そして、まったく偶然に5°18´という角度の正割の値を調べてみる。すると、半径EB＝１に対して、斜辺EAは1.00429になった。正割EA＝1.00429である。1.00429－1＝0.00429で、三日月の幅の値と対応するではないか。ここで、ケプラーは新たな光を見たのだと思う。

枇杷とひよどり

先週の金曜日に今季2度目の雪が降った。土曜日の朝、2階の部屋から。