ハミルトンの止揚

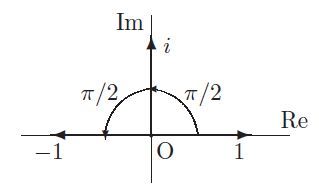
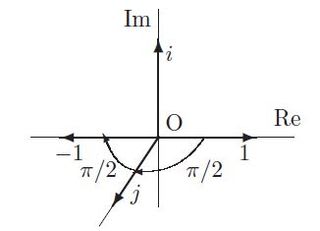
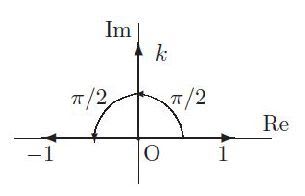
ハミルトンは空間ベクトルを4元数の虚部と同定した。これをハミルトンの止揚とよんでみよう。そのこころは?

ハミルトンは平面のベクトル「複素数」（2元数）と対応させて空間ベクトル「3元数」を構想した。
簡単にたどってみよう。
2元(1,i)
↓　第3の元jの発見
3元(1,i,j)
↓　第4の元kの発見
4元(1,i,j,k)
↓　虚部に着目
3元(i,j,k)

3元の間に着目すると、
3元(1,i,j)
↓　4元 (1,i,j,k)
3元(i,j,k)
ハミルトンは1を「止」めて、kを「揚」げたのである。

飛騨古川 on ゼロの焦点

2009年に「ゼロの焦点」（広末涼子主演）が公開されていたとき、見に行った。金沢が舞台になっていたが、金沢の旅館と旅館近くの風景に見覚えがあった。飛騨古川の「八ツ三」、荒城川、霞橋。古川がロケ地になっているとは思わず（映画の最後にロケ地の紹介があった）、金沢にも同じ名前の旅館があるのかと思ってみていた。今週の火曜日にNHKのBSで「ゼロの焦点」をやっていた。録画をみると、瀬戸川沿いも映っている。旅館の近くも瀬戸川沿いも映画用に装飾されていた。飛騨古川（飛騨市古川町）はとてもいい町に見えるのだった。

午後のラジオ体操

朝6時30分の体操が基本だった。明るくなってきて、この時間で再開してもよいのだが、起きられない。これまで第1放送に周波数をあわせていたが(729)、いまは第2である(909)。8時40分、12時、15時。3回のうち1回が基本。2回やった日もある。朝は「歌」があるが、午後はない。その分、体操の時間が少し長い。朝は「おはようございます」で始まったが、昼は「こんにちは」である。午後の放送は朝の再放送ではなかった。

台所で焼き芋

以前、庭で芋を焼いた。今日も炭をおこして焼くつもりだった。ところがうまく炭がおきないし、時間がかかりすぎると思った。台所で焼けるか試そうと思った。初め、オーブン（電気）でやってみたが、1000Wでも火力が弱い。それで魚を焼くグリル（ガス）でやってみた。30分ほど焼いたが、ホクホクだった。これは使える。後で検索してみると、魚焼きグリルで焼き芋のレシピはいくつも公開されているのだった。

かかと落とし

骨を刺激して骨ホルモンを分泌させて臓器を活性化する。すい臓を元気にして、血糖値の改善をしたい。そう思って始めた。刺激が伝わっていく感じが心地よい。かかと落としは、骨粗しょう症の対策としても効果があると記事にある。また、かかとには生殖腺の反射区がある。かかと落としによって、ここを刺激することにもなる。簡単な運動だが、さまざまな効果が期待できる。

2つの公式の違い

ハミルトンは1843年10月16日、２種類の公式を書いている。
朝、手帳と橋の欄干に書いたもの。
i²=j²=k²=ijk=-1
夜、ノートに書いたもの。
i²=j²=k²=-1
ij=k,jk=i,ki=j
ji=-k,kj=-i,ik=-j

この２つの式は４元数の公式として同じものである。しかし、朝の1行の式は「ことの重大性が一瞬に感じとれたこと」、「電気の回路は閉じ、閃光がひらめいた」（An electric circuit seemed to close, and a spark flashed forth.）と形容されているものである。この2つの公式の違いは何なのだろうか。比喩的にいえば、朝の式は迷いのなかでみた光であり、夜の式は悟りのなかで輝く光といえばよいのではないだろうか。

ノートには研究の経緯が述べられている。そのなかで注目すべきは、3元数の積について、特殊な場合と一般的な場合では違いがあったことである。
特殊な場合、
(x+iy+jz) ²
(a+iy+jz)(x+iy+jz)
では、これらはij=0やij=-ji（iとjだけで閉じている）の仮定だけでも3元数は成立していた。
これに対して、一般的な３元数の積
(a+ib+jc)(x+iy+jz)
を考えた場合は、3元では収まらず、「積ijが新しい虚数、ji=-kとしたときのkになるのではないか」という考えがあったことである。4元数が隠顕していたのである。

朝の式の核になっているのはijk=-1である。この式がどのように現れたのかは「謎」（ハミルトンにとっても）である。しかし、この式の中でij=0が成立しないことは明確である。ハミルトンにとってij=0（やij=-ji）は空間のベクトルを3元（1,i,j）で完結させたいという要請・願望・先入観の表現である。
ijk=-1の出現によって、この道が消えたのである。いいかえれば3元数の積は3元では表現できず、第4の元を導入せざるを得ないことが明確になったのである。ijk=-1はij=0を排除して4元数と直面させた。「迷いのなかでみた光」というゆえんである。
しかし、迷いはすぐになくなったわけではない。ノートを読むと、ijk=-1を自覚した後でも、ij=0の可能性に対する未練は残っていたことがわかる。ハミルトンは次のように述べている。
（引用はじめ）
未だに（そしてたぶん前にも）ij=0になることは可能ではないか、と考えていた:そして（朝の思考過程を夜になって思い出そうと試みて）私は信ずるに、この等式ij=0が真であることが分かるのが、奇妙かもしれないが、もっともらしいとさえ考えた
（引用おわり）
感動的な告白ではないか。3元だけで完結させたいという気持ちはそれほど強かったのである。しかし、この後、ハミルトンは気を取り直して、3行のほうの公式を「仮定もしくは定義」として書き下ろしている。
そして、一般的な4元数の積において「乗積の絶対値が絶対値の乗積に等しい」ことを確認し、4元数に拡張したオイラーの公式を導いている。そこでノートは終わっている。

参考文献
『ハミルトンと四元数』（堀源一郎著、海鳴社、2007）1章、2章（ノート）
『四元数の発見』（矢野忠著、海鳴社、2014）2章、3章（ノートの解読）

拡張

2元から４元へ。出発点にもどれるように拡張されていて感動する。

2次式の因数分解（共役に着目）
a²+b²
=(a+bi)(a-bi)
a²+b²+c²+d²
=(a+bi+cj+dk)(a-bi-cj-dk)

オイラーの公式（虚数単位などに着目）
e^ix
=cos x + i sin x
e^ix+jy+kz
=cos √(x²+y²+z²) + (ix+jy+kz)/√(x²+y²+z²) ･ sin √(x²+y²+z²)

骨ホルモン

NHKためしてガッテン!をみていて勇気づけられた。
骨を上手に刺激すると骨からホルモンが出て全身へ運ばれ、脳・肝臓・すい臓・腎臓などの臓器を活性化することがわかってきたという。血液中の骨ホルモン（オステオカルシン）の量が少ない人は、血糖値が高い傾向にあるのだという。
番組は、骨を上手に刺激する運動として「かかと落とし」を勧めていた。これは直立した姿勢からゆっくり真上に伸びあがり一気にかかとを落とす運動。これを１日３０回以上を目標にやるといいのだという。
ラジオ体操の後でやることにした。

幻視のなかの橋2（改訂）

４元数の考察を始めたが、途中から「幻視のなかの橋」というイメージが出てきた。幻視のなかの橋2は、すでに書いていた記事（2つの原則、2元数と3元数、3元数の積）を前提にしていたので、「幻視のなかの橋」の2としては不十分なものになっているように思えた。幻視のなかの橋2を以下のように改訂する。

幻視のなかの橋2

2.1　i²=j²=-1　
複素数の二つの元1とiは次のように表示される。元1を原点Oを中心にしてπ/2=90°回転した位置に元iがある。このiをπ/2=90°回転すると-1が得られる。複素数（2元数）a+biは実軸Re(x軸)、虚軸Im(y軸)の平面上の点(a,b)を表わす。

ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づいた。iがxy平面を回転するのに対して、jはxz平面を回転して－1になる。j²=-1である。j²=i²だが、jはiではない。3元数a+bi+cjは実軸Re(x軸)、虚軸Im(y軸)、虚軸I'm(z軸)の空間の点(a,b,c)と対応するのではないか。これがハミルトンの出発点だった。

図は矢野忠「四元数の発見へ」（『数学・物理通信』1巻11号）より

2.2　２つの原則
ハミルトンが複素数から類推して3元数を構想したとき、端的にいえば、2つの原則があった。
1　体の原則　加減乗除について閉じていること
2　絶対値の原則　絶対値の乗積は、乗積の絶対値に等しいこと
　 |p||q|=|pq|
複素数で2つの原則を確認しておこう。
1　かけ算（だけ）で確認する。複素数同士のかけ算の結果は複素数になる。閉じている。
(a+bi)(x+yi)=(ax-by)+(ay+bx)i
2 |p|²|q|² =|pq|²で確認する。
p=a+bi , q=x+yi,pq=(ax-by)+(ay+bx)i
(a²+b²)(x²+y²)=(ax-by) ²+(ay+bx) ²　成り立っている（ラグランジュの恒等式）。
２つの原則は複素数において成立している。
3元数a+bi+cjとx+yi+zjはどうだろうか。
注
(ax-by) ²+(ay+bx) ²
=a²x²-2abxy+b²y²+a²y²+2abxy+b²x²
=a²x²+b²y²+a²y²+b²x²
=a²(x²+y²)+b²(x²+y²)
=(a²+b²)(x²+y²)

2.3　ij=-ji=kの可能性
3元数a+bi+cjとx+yi+zjの積をみる。
(a+bi+cj)(x+yi+zj)
=(ax-by-cz)+(ay+bx)i+(az+cx)j+bzij+cyji
下線部の項によって3元数の積は3元数にはならない。ij=X+Yi+Zjと変形できるとも思えない。閉じていない。3元数は体の原則を満たしていないのである。
下線部を0とみなして、絶対値の原則と照らし合わせてみる。
(a²+b²+c²)(x²+y²+z²)=(ax-by-cz)²+(ay+bx) ²+(az+cx)²
この式は成り立っていない。左辺は右辺より(bz-cy)²だけ大きい。
すなわち、
(a²+b²+c²)(x²+y²+z²)=(ax-by-cz)²+(ay+bx) ²+(az+cx)²+(bz-cy)²
なら成り立つのである。
このbz-cyは下線部bzij+cyjiと密接に関係している。すなわち、ij=-jiと想定するとbzij+cyji=(bz-cy)ijである。
いま、3元1,i,jに加えて第4の元が見え隠れしている。ij=-ji=kとおこう。

2.4　k²=-1
i²=-1,j²=-1を基礎にk²の値を調べてみよう。
k²=(ij)²=ijij=-i(ij)j=-iijj=-i²j²=-1
i²=j²=k²=-1である。虚数単位として整合的ではないか。単独で図示すれば次のようである。

これは２元の図でiにkを重ねた図である。こちらは問題はない。
だが、1,i,jの関係と連立させて図示するとどのようになるのだろうか。

これは3元の図で1にkを重ねた図である。実軸は虚軸に隠れている。1とkは下の図では重なって見えるが、角度を変えて見ると上のように1とkは垂直である。

東西南北を意識する

日本では、衛星放送（BS）のアンテナ（円盤状のパラボラアンテナ）は必ず南西の方向を向いている。放送衛星はフィリピン・ボルネオ島の上空に静止して地球と同じ速さ回っている。南西に向けて設置しないと、その電波を受けとれないからである（『図解よくわかる計り方の事典』星田直彦著、参照）。
庭に出て北の方向を見ていた。近くの屋根の上のアンテナの側面が左前方45度の方向に見えた。たしかに南西を向いていると思った。他のアンテナの向きも確認していると、東の方から西に向かって自衛隊機が３機、かなり低空を飛んで行った。