千両と万両

雪は降らなかったが、寒い一日となった。昨年の末に撮った赤実と白実の万両を見に行くと、どちらも実の付きが悪く、白の方は数粒ついているだけだった。今年は千両もだめだったが、万両の方はもっとひどい結果になっていた。赤と白の対照はあきらめて、他の対照を求めて庭を歩いた。


今年は平均すると130人ほどの方にみていただきました。ありがとうございます。今年はここまでにします。どうぞよい年をお迎えください。

「アブダクション」を振り返る

カテゴリー「アブダクション」をつくり、パースのアブダクションについて、考察を進めていくつもりだったが、失速してしまった。

1、パースのアブダクションは「通常科学」の推論で、「科学革命」の推論ではないように思われた。それでアブダクションを拡張する必要があると思った。「演繹モデル」の前に「帰納」を導入すればよいと考えたが、展開しきれなかった。
2、帰納とアブダクションの関係が明確にならなかった。
パースは「論文集」（『世界の名著』所収）で次のように述べていた。
（引用はじめ）
どんな演繹的推論もつぎのような公式にはめこむことができる。「もしAならばB。しかるにA。ゆえにB」。ところでこの公式における小前提Aは、大前提である仮言命題のなかに、その前件として出現している。したがって推定的推論（アブダクションのこと、注）は後件から前件への推論とよぶことができる。
（引用おわり）
これは米盛裕二や池上嘉彦（『記号論への招待』）が定式「Bである。AならばBである。ゆえにAである」をアブダクションの定式として捉えていることと対応している。しかし、ポリアも瀬山士郎もこの定式を「帰納」と捉えている。ここがうまく説明できなかった。
3、演繹・帰納・アブダクションと記号の1次性・2次性・3次性の関係をつかみたかったが、パースの記号論が難しく進まなくなってしまった。

蛇の髯の實の瑠璃なるへ

蛇の髭（ジャノヒゲ）の葉が拡がって座布団のようになっている。根元の実を探して、葉をかき分けていると、すぐそばの葉の上に乾いた糞があった。危なかった。猫の糞である。庭に何匹か猫がやってくる。野良猫ではなく、近所で飼われている猫である。
タイトルは中村草田男の俳句からである。「蛇の髯の實の瑠璃なるへ旅の尿」。蛇の髭の実が冬の季語である。中村は立小便をした。ここでは猫が糞をした。どちらも切羽詰まっていたのだろう。

「ピントレ」は続いている

1度、挫折したが、続けている。2人の方にコメントをいただき、頑張ろうと思った。ピンク色の付箋に「ピントレ」と書いてテレビの画面の横に貼って注意を喚起している。ルーティンを決めたことが、続いている理由だろうか。

目覚まし時計（アナログ）を机の上に置き、テレビを見ながら始める。
しゃがみ込むときにボールペンを椅子の座面に、横、縦、横……と置きかえて、座面に「正」の字を描いていく。これを2回繰り返すと、10回の屈伸になる。9回目、10回目のときの腿の筋肉の緊張がたまらない。正確に数える必要はないが、これがよかったように思う。しばらく休んで、繰り返す。休まないとできない。
最初に試みたときは、初めの10回で、もう汗が出てきたが、このごろは少し遅くなって、20回、30回で汗ばんでいる。
15分から20分の運動である。ラジオ体操より長く、早歩きより短い。2日ほど休んで、1週間に2度のペースでやっている。

赤実の千両

庭の花を確認する。水仙と南天は正月の飾りに十分まかなえるが、赤実の千両は少し心もとない。

鼻水がとまらなくなった

愛知県図書館に行って来た。名古屋駅では宝くじの行列ができていた。いつものように名古屋駅近くの本屋をのぞいてから、図書館まで歩いた。前回から昼食を用意している。前は近くの公園で食べたが、今回は館内に用意してあるスペースを利用した。時間にもよるだろうが、老若男女、ほぼ満室だった。いつもは帰りも名古屋駅まで歩くのだが、今日は地下鉄を利用した。調子が悪くなったのである。鼻水が出てきて、とまらなくなってしまった。風邪ではなく、おそらく本のほこりが原因だと思う。一冊、閉架の本で、古いのがあったのである。これがきっかけだったと思う。今は回復している。
今日借りた本を返却するのは新年になってからになる。

数学的帰納法のプリンキピアモデル

数学的帰納法の解説にはドミノ倒しがよく持ち出される。たしかに、ドミノ倒しは自然数という数のシステム（1からはじまり1ずつ増えていく）の特徴と対応していて、数学的帰納法はドミノ倒しの論法といっていいだろう。
　1　2　3　･･･　n　n＋1　n＋2　･･････
しかし、ドミノ倒しの＋1は、直線的で単調で、数学的帰納法で核心となるnからn＋1への移行の重要性を減じているように思われる。それはnからn＋1への飛躍を単調な＋1へと還元している。
パスカルが「数三角形」で踏み出した小さな一歩は数学にとって大きな一歩になった。それはドミノ倒しの単調な一歩ではないように思われた。違った比喩、単調な連鎖の中に埋没しているnからn＋1への＋1の重要性に注意が向くような比喩はないのだろうか。それはパスカルが踏み出した小さな一歩を大きな一歩とみる比喩である。

数学的帰納法のプリンキピアモデルというのは、ニュートンがプリンキピアで示した次のような図を数学的帰納法と対応させるものである。

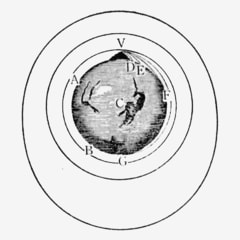
端的にいえば、nからn＋1への移行に、放物線から楕円への移行を対応させ、nからn＋1の移行を特別視するものである。

このモデルはわたしが思いついたものではない。ポリアが『数学における発見はいかになされるか1帰納と類比』（柴垣和三雄訳、丸善株式会社、1959年初版、1974年5版）で提起しているものである。
（引用はじめ）
一つの推測を検査するとき、われわれは、それが当てはまると想像される幾つかの事例を研究する。われわれは推測によって主張される関係が安定であるかどうか、すなわち、事例の変動に無関係でそれによって乱されないかどうかを知りたいのだ。われわれの注意はこうして自然に、一つのそのような事例から他の事例への移行に向けられる。「遠心力によって遊星がある軌道に束縛されることは、発射体の運動を考えれば容易に理解できる。」とニュートンは述べ、それから彼はついに月の軌道のように地球のまわりを回るようになるまで次第次第に増大する初速度をもって発射される石を想像する。（上の図を見よ。）こうしてニュートンは発射体の運動から遊星の運動への連続的移行を目に浮かべる。彼は、彼が証明しようと企てた万有引力の法則が同様にあてはまるはずの、二つの事例の間の移行を考える。ある初等的定理を証明する際に数学的帰納法を用いる初学者は、この点に関してはすべてニュートンのようにやるわけである。彼はnからn＋1への移行、彼が証明しようと企てた定理が同様にあてはまるはずの、二つの事例の間の移行を考えるのである。
（引用おわり）
ここで数学的帰納法を用いる初学者とは、17世紀のパスカルであり、現代の高校生である。このモデルは魅力的に思えた。しかし、無限に連続する自然数の列とこのモデルはそのままでは対応しているようには思えなかった。そこで、nとn＋1の間に断絶を導入し、その前後を分けて、自然数の列にいわば構造を想定してみた。
　1　2　3　･･･　n　n＋1　n＋2　･･････
1は鉛直落下である（リンゴは落ちる）。2　3　･･･　n　は射程を伸ばしていく放物線である。n＋1　n＋2　･･････は楕円（月は落ちてこない）である。
このような対応を想定していたが、何か人工的で自然ではないように感じていた。不自然な自然数の列を感じて一歩踏み出せなかった。

しばらく足踏みが続いたが、新井紀子著『数学は言葉』で数学的帰納法の別のバージョンがあることを知った（注）。これまで馴染んでいたのは自然数と等置されたペアノ版であった。これは「ドミノ倒し」と正確に対応する。別のバージョンは有限集合を基礎にする数学的帰納法であった。人工的に導入した断絶がおのずと有限集合から無限集合への境界としてそのまま存在し、その境界を越えることがそのまま数学的帰納法の証明になるように思われた。いままで不自然な自然数の列と見えていたものが、自然な自然数の列に見えてきた。いいかえれば、数学的帰納法の別のバージョンはプリンキピアモデルと対応するのではないかと思われてきたのである。

もう一歩進んでみよう。

（注）
「数学的帰納法の別バージョン」
　自然数nに関する性質Q(n)について、次の2つのことが示されたとする。
　　(1)　Q(1)が正しい。
　　(2)　任意の自然数k＜nについて、Q(k)が正しいと仮定すると、Q(n)は正しい。
　このとき、任意の自然数nについて、Q(n)は正しい。

サザンカを見上げる

午前中は、ナンキンハゼの木を切り倒した。道路沿いにあるので、庭の方に倒れるように注意した。枝は束ねた。幹の方は、40センチほどの長さに切断した。6つの断片が庭に転がっている。こちらの始末は明日以降である。チェーンソーになれてきたなあと実感した。少し前に、背の低い唐棕櫚、幹だけになっていた楠を整理したので、道路沿いはすっきりしてきた。近所の人によると、家には風通しがよくなるのが一番いいらしい。
あと道路沿いにはクロガネモチ、イロハモミジ、カキ、サザンカがある。クロガネモチはいずれ切り倒す。柿と山茶花は残す。イロハモミジは迷うなあと考えながら、道路にでて、サザンカを見上げた。

数学的帰納法、2つのバージョン

新井紀子は『数学は言葉』で次の3つの公理は互いに同値であるといっている。
（引用はじめ）
1.　数学的帰納法
2.　任意の自然数について、nより小さい自然数全体の集合は有限集合である。
3.　自然数nに関する性質Q(n)について、次の2つのことが示されたとする。
　　(a)　Q(1)が正しい。
　　(b)　任意の自然数k＜nについて、Q(k)が正しいと仮定すると、Q(n)は正しい。
　このとき、任意の自然数nについて、Q(n)は正しい。（数学的帰納法の別バージョン）
（引用おわり）
数学的帰納法の中身は次の通り。
1.　自然数nに関する性質Q(n)について、次の2つのことが示されたとする。
　　(a)　Q(1)が正しい。
　　(b)　任意の自然数kについて、Q(k)が正しいと仮定すると、Q(k＋1)が正しい。
　　このとき、任意の自然数nについて、Q(n)が正しい。
バージョンの違いは(b)の表現である。新井紀子の高校生へのアドダイスは1.の数学的帰納法、瀬山士郎のは3.の数学的帰納法の別バージョンを背景にしていると思う。

どちらもkからk＋1への移行に着目することになるが、＋1の移行が、1.では最初からどれも同じ大きさの＋1である。一方、3.では、Q(n)を示すときの＋1はそれまでの＋1とは違う大きさをもつ印象を受ける。また、1.では無限集合だけを見ているが、3.では有限集合を基礎にした無限集合を見ることになる。
わたしはパスカルの『数3角形』で示されている数学的帰納法を3.のように捉えてきた。それは有限集合から無限集合へと拡張する数学的帰納法である。これがオリジナルバージョンだったと思う。これを数学的帰納法のパスカル版としよう。
これに対して、1.は改訂され整理された数学的帰納法である。数学的帰納法のペアノ版というところだろうか。

ペアノ版は「ドミノ倒し」と相性がいい。パスカル版はどうだろうか。同値な命題だから、「ドミノ倒し」は否定できない。しかし、別のバージョンだから、「ドミノ倒し」とはちがったモデルを提起する余地はあるだろう。これをやってみよう。

数学的帰納法、高校生の誤解

数学的帰納法を学ぶ高校生のなかには、これで証明になっているのかと疑問をもつ者がいる。この疑問は数学的帰納法の誤解から生じているが、誤解を取り上げその原因を示している本があった。1つは新井紀子『数学は言葉』（東京図書、2009年）、もう1つは瀬山士郎『なっとくする数学の証明』（講談社、2013年）である。
1『数学は言葉』
数学的帰納法は次のような命題としてまとめられている。
〈数学的帰納法〉
自然数nに関する性質Q(n)について、次の2つのことが示されたとする。
1.Q(1)が正しい。
2.任意の自然数kについて、Q(k)が正しいと仮定すると、Q(k＋1)が正しい。
このとき、任意の自然数nについて、Q(n)が正しい。
これに対する高校生の疑問は次のようなものである。
「任意の自然数kについて、Q(k)が正しいと仮定する」ならば、「任意の自然数nについて、Q(n)が正しい」は決まっている。なぜこれで証明になっているのだろう。
新井紀子は数学的帰納法を数文に訳す。
　(Q(1)∧∀k(Q(k) → Q(k＋1)))　→　∀nQ(n)
そして、次のように指摘する。
（引用はじめ）
仮定に登場する量子化∀は、Q(k)だけにかかっているのではなく、(Q(k)→Q(k＋1))全体にかかっていることがわかります。「任意の自然数kについて、Q(k)が正しいと仮定」しているのではなく、「任意の自然数kについて、Q(k)→Q(k＋1)が正しいと仮定」しているのです。ここを誤読しないようにしましょう。
（引用おわり）
2『なっとくする数学の証明』
疑問は次のようである。
もう1つ、高校生の疑問に答えておきます。数学的帰納法で、「P(k)が正しいと仮定すればP(k＋1)が正しい」の部分です。一般のkについてP(k)が正しいと仮定するなら、なにもP(n)が正しいことを証明する必要がないのではないかという疑問です。
これに対して、瀬山士郎は新井紀子とは違った角度から次のように注意している。
（引用はじめ）
このkは一般のnではありません。仮定しているのは、k以下の自然数nについて命題P(n)が成り立つということで、kより大きな自然数については命題が成り立つかどうかわからない。しかし、kまで仮定すれば、もう一つ大きなk＋1まで命題が成り立つことが分かるという意味です。ですから、帰納法の第2ステップを、
　(2)　k以下のnについて、P(n)が正しいと仮定するとP(k＋1)も正しいことを証明する。
と表現すると分かりやすいのだと思います。ですが、普通はこれを
　(2)　Ｐ(k)が正しいと仮定するとP(k＋1)も正しいことを証明する。
と表現するのです。
（引用おわり）
両者の高校生に対するアドバイスはどちらも正しいと思われるが、その説明の違いには、数学的帰納法のバージョンの違いが背景にあるようだ。
これを見ておこう。