楕円軌道の発見におけるプトレマイオスとケプラーの関係は、弁証法発見のヘーゲルとマルクスの関係と対応しているのではないか。このように考えはじめていた。プトレマイオスが導入した「離心距離の二等分」は神秘的な外皮に隠されている。プトレマイオス惑星理論の「合理的核心」を把握するにはひっくり返さなければならない。
コペルニクスは天地を転倒し、惑星軌道は地球中心から太陽中心に変わった。ケプラーはこの惑星軌道で「離心距離の二等分」を継承し、楕円軌道を発見する。楕円発見の過程はすでに見てきた(「楕円軌道の発見」参照)。ここではプトレマイオスとケプラーの関係に焦点を当てることにする。
ケプラーが楕円を発見する火星の軌道に、プトレマイオスが金星で導入した等化点と等化円を描いてみる。『新天文学』の火星と『アルマゲスト』の金星をつないでみるのである。プトレマイオスの等化円の特徴は、遠日点で離心円に内接していて、離心円の中心が等化点と離心点を二等分していることだった。離心円の半径を1、離心率をeとすると、等化円の半径は1-eである。
ケプラーが『新天文学』第32章で描いた等化円は離心円と同じ半径だった(「速さと遅さ」参照)。その等化円を1-e 対1の比で縮小し、遠日点Hで内接させてみる。楕円軌道も描いてある。
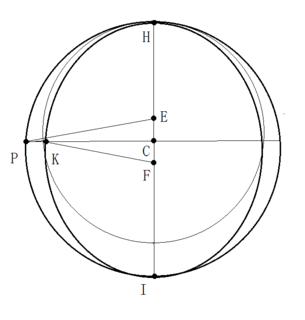
Fは離心点、Cは離心円の中心、Eは等化点である。等化円は細い線で描いてある。Hは遠日点、Iは近日点である。PとKは楕円軌道発見の現場で、「平均的な長さを取るところでは正割の代わりに半径を用いる」箇所である。Pは離心円上の点、Kは楕円上の点である。
長さを見ておこう。離心円の半径CH=CP=CIを1、離心率をeとする。CF=CE=e、EH=1-e、EI=1+eである。
PE は直角三角形PCEに三平方の定理を適用して
PE =√(1+e
2)となる。
この
PE は「離心距離の二等分」より
PF に等しい。ケプラーが使った火星の離心率eは0.009265で、√(1+e
2)を計算してみると1.00429になる。これが正割の値に対応している。ケプラーを目覚めさせた正割は、遠日点から90°離れた離心円上の点Pとプトレマイオスが導入した等化点Eとの距離に対応する。楕円発見の端緒には「離心率の二等分」が背景にあった。(注)
ケプラーは正割の代わりに半径を用いる。すなわち、
PF =1.00429ではなく
PC =1を用いる。これが端緒だった。Fを中心に半径1で弧を描きPCとの交点をKとする。それが正しい火星の位置である。
KF =1である。直角三角形KCFに着目し、三平方の定理を使うと、
KC =√(1-e
2)である。これが楕円の短半径となる。
離心点Fと等化点Eは全く動いていない。離心点Fと等化点Eは離心円の中心Cによって二等分されたまま、離心円から三日月形が切り取られることによって、楕円の焦点となっている。「離心距離の二等分」は自然の秘密の鍵であり、プトレマイオス惑星理論の「合理的核心」だったのである。
(注)
「100429の数学的背景」では、離心円上にある惑星と太陽の間の距離を離心アノマリア
βを使って求め、べき展開して近似式を導いた。それは離心率
eの2次までの近似で次のようになった。
r=1+
ecos
β+
e2/2・sin
2β
β=90°を代入したときがPFの距離になる。
PF = 1+
e2/2
ここに火星の離心率e=0.09265(ケプラーの値)を代入して、1.00429を導いた。
しかし、ここでは、等化点Eと離心円上の点Pとの距離
PE と「離心率の二等分」という仮定だけを使っている。離心円上の1点Pだけに着目した展開だが、興味深いと思われる。(だれかこれまでに指摘しているだろうか。)
√(1+
e2)をべき展開すると
1+1/2・e
2-1/8・e
4+…
となり、2次までとると
1+
e2/2
となり、同じ結果を与えることがわかる。













 1プトレマイオス
1プトレマイオス 2太陽中心系
2太陽中心系 3ケプラー
3ケプラー


