数学で
nC
rといえば、n個の異なるものからr個とる組合せの数である。Cはcombination(組合せ)のイニシャルである。また、
nC
rはn次の二項展開式におけるr次の項の係数である。この場合のCはcoefficient(係数)だろう。
この2つのCはパスカルの数三角形と密接に関係している。ここで、パスカルの数三角形における細胞の位置と数を示す表記として、もうひとつ
nC
rを考えてみよう。この場合のCは細胞(cell)のCである。
| 0C0 | 1C1 | 2C2 | 3C3 | 4C4 | 5C5 | 6C6 | 7C7 | 8C8 | 9C9 |
| 1C0 | 2C1 | 3C2 | 4C3 | 5C4 | 6C5 | 7C6 | 8C7 | 9C8 | |
| 2C0 | 3C1 | 4C2 | 5C3 | 6C4 | 7C5 | 8C6 | 9C7 | | |
| 3C0 | 4C1 | 5C2 | 6C3 | 7C4 | 8C5 | 9C6 | | | |
| 4C0 | 5C1 | 6C2 | 7C3 | 8C4 | 9C5 | | | | |
| 5C0 | 6C1 | 7C2 | 8C3 | 9C4 | | | | | |
| 6C0 | 7C1 | 8C2 | 9C3 | | | | | | |
| 7C0 | 8C1 | 9C2 | | | | | | | |
| 8C0 | 9C1 | | | | | | | | |
| 19C01 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 |
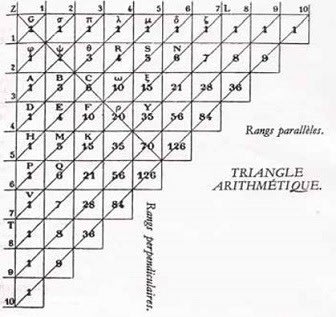
数三角形の数は、次の規則で規定されたものである。
「各細胞の数はその垂直行における直前の細胞の数とその水平行における直前の細胞の数との和に等しい。」
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | | |
| 1 | 4 | 10 | 20 | 35 | 56 | 84 | | | |
| 1 | 5 | 15 | 35 | 70 | 126 | | | | |
| 1 | 6 | 21 | 36 | 126 | | | | | |
| 1 | 7 | 28 | 84 | | | | | | |
| 1 | 8 | 36 | | | | | | | |
| 1 | 9 | | | | | | | | |
| 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 | 111 |
例えば、色付きの部分。
これは
5C2=
4C1+
4C2
である。
一般に、次のような規則で並べてある。
nC
r=
n-1C
r+
n-1C
r-1
これは組合せの公式として馴染みがあるものだが、ここで配列の規則である。
このような数三角形の数の配置からさまざまな規則をパスカルは読み取っていく。なかでも核心は三角形の底辺(斜め)で隣り合う2細胞の数の比例関係である。
「あらゆる数三角形において、同じ底辺にあって隣接する2つの細胞のうち、上位の細胞と下位の細胞との比は、上位の細胞から底辺の最上段までの細胞の個数(両端の細胞を含む)と、下位の細胞から最下段までの細胞の個数(両端の細胞を含む)との比に等しい。」
例えば、赤字の部分。
6(上位の細胞
4C
2の数)と4(下位の細胞
4C
1の数)の比は、3(上位の細胞から底辺の最上段までの細胞
4C
2・
4C
3・
4C
4の個数)と2(下位の細胞から最下段までの細胞
4C
1・
4C
0の個数)に等しい。
(つづく)