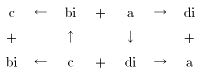シロハラ

しばらく前から、見なれぬ鳥が庭に来るようになっていた。ムクドリとも違うし、ツグミとも違う。地面をぴょんぴょん跳ねて何かをついばんでいたり、枝にとまったりしていた。人をあまり恐れない。近づいても何かおっとりしている感じである。飛んでいるとき、尾羽に白いものが見える。シロハラではないかとあたりをつけていた。今日、洗濯物を取りこむとき鳥の鳴き声が聞こえた。キョッ、キョッ。見ると花桃の枝に止まっている。これで確定できると思った。たしかにシロハラであった。冬はほとんど鳴かず、たまに小声で地鳴きする程度とある。ラッキーだった。


今年は平均すると80人ほどの方にみていただきました。ありがとうございます。2016年はこれで最後です。
では、みなさま、どうぞよい年をお迎えください。

「オイラーの公式と弁証法」

「オイラーの公式と弁証法」（はじめに）より。

オイラーの公式は数学で最も美しい式といわれている。たんに美しいだけでなく、実用的にもすぐれている。それは異なる種類の2つの関数、指数関数と三角関数を結びつけるもので、次のような式で表わされている。
　　e^ix = cos x+isin x
遠山啓はこの式を「太平洋と大西洋を結ぶパナマ運河」と形容していた。また吉田武は「虚」と「実」、「円」と「三角」を結ぶ「不思議の環」と形容している。ファインマンは「jewelry(宝石)」とよんでいた。
この公式は18世紀にオイラーが導いたものである。異なる指数関数と三角関数が結ばれているので、この公式が作られた過程は弁証法と対応しているのではないかと思われた。ここで弁証法とはギリシアやヘーゲル、あるいはマルクス主義の弁証法ではなく、私が提起している弁証法のことである。それは端的にいえば、2つの「論理的なもの」を選んで1つの「論理的なもの」にまとめる技を指している。『オイラーの無限解析』（レオンハルト・オイラー著/高瀬正仁訳/海鳴社）と『無限のなかの数学』（志賀浩二著/岩波新書）を参考にして、オイラーの公式が作られた過程を把握したいと思う。

「オイラーの公式と弁証法」（PDF）
目次
1　はじめに
2　指数関数とn倍角の公式
3　n倍角の公式への極限の導入
4　指数関数への虚数単位の導入
5　オイラーの公式
6　公式の導出と弁証法との対応
付録
1　オイラーによる虚数単位iを用いたn倍角の公式の導出
2　オイラーによるsinとcosの巾級数展開の導出
3　「論理的なもの」
　　1　自己表出と指示表出
　　2　複素数モデル
4　弁証法の理論
　　1　「対話」の基礎
　　2　「対話」のモデル
　　3　「止揚」のモデル
　　4　ひらがな弁証法
参考文献
「オイラーの公式と弁証法」（PDF）

オイラーの公式、再論。

『無限のなかの数学』（志賀浩二著/岩波新書）を読んでいるとき、オイラーの公式が導かれた過程は弁証法の新しい考え方（複合論）で捉えられるのではないか思われた。『オイラーの無限解析』（レオンハルト・オイラー著/高橋正仁訳/海鳴社）の関連する個所を読んでみたが、オイラーの発想と複合論は対応しているのではないかという思いは強くなっていった。2005年に「オイラーの公式と複合論」を書いた。
今年（2016年）の10月ごろから、LaTexの修業をかねて、「オイラーの公式と複合論」を見直しはじめた。「論理的なもの」や「弁証法」についての認識や表現があいまいだったので、その後、現在の立場から「論理的なもの」や「弁証法」についていくつか記事を書いてきた。
いま「オイラーの公式と弁証法」というタイトルで「オイラーの公式と複合論」の改訂版をLaTexで書いている。「論理的なもの」や「弁証法」についての説明は、本文ではなく脚注と付録に移した。また、「虚数単位を用いた n 倍角の公式」の導出も本文ではなく付録に移した。これでオイラーの公式が導かれた過程が前面に出ると思う。また今回、文献を読み直していて、オイラーが「虚数単位を用いた n 倍角の公式」からsinとcos の巾級数展開を導いていることを知った。これが公式を導く重要なステップになっていた。これも付録に入れている。

弁証法は27のひらがな。

ひらがな弁証法を提起している。「ひらがな弁証法2010」
弁証法は2つの「論理的なもの」から1つの「論理的なもの」にみちびく技である。これを次のように表示してきた。
あれとこれと
むすんでひらいて
ふたつをひとつに
つなぐわざ
「あれとこれと」は2つの「論理的なもの」、「むすんでひらいて」は弁証法の場所的構造、あれとこれの可能性がひろがっていくかたちを表わしている。これは「対話」をとりいれたものである。「ふたつをひとつにつなぐ」は弁証法の過程的構造で、「止揚」をとりいれたものである。
先日、LaTexで記事を書いていた。見た目は上のように改行してあるのだが、DIVで閲覧してみると1行で表示されていた。これが新鮮だった。石の記念碑に刻んでおきたい気分になった。あれとこれと6、むすんでひらいて8、ふたつをひとつに8、つなぐわざ5。ひらがな27。
　　あれとこれとむすんでひらいてふたつをひとつにつなぐわざ

弁証法の複素数モデル

複素数のかけ算、
Ａ×Ａ'
＝（ａ＋ｂｉ）×（ｃ＋ｄｉ）
＝（ａｃ－ｂｄ）＋（ａｄ＋ｂｃ）ｉ
＝ｘ＋ｙｉ
＝Ｂ
は、2つの異なる複素数から1つの複素数が出てくる過程を表わしている。これを2つの異なる「論理的なもの」から1つの「論理的なもの」が形成される過程のモデルとした。
2つの「論理的なもの」を出発点にして、その自己表出（ａとｃ）と指示表出（ｂiとｄi）が関連しあい、新しい自己表出（ａｃ－ｂｄ）と指示表出（ａｄ＋ｂｃ）iをもつ「論理的なもの」が形成される過程を表わしている。これは『もうひとつのパスカルの原理』で提起した複素過程論で、ケストラーの創造活動の理論バイソシエーションbisociation（二元結合）のモデルとみることができるものである。
しかし、上に示した複素数のかけ算は数学の公式通りの展開である。その意味では同じレベルでの展開であり連続している。この複素数のかけ算を基礎に「対話」と「止揚」を導入して非連続化する。これが弁証法の複素数モデルになる。
「対話」の導入は次の図式で表示できる。
「ひろがるかたち」（弁証法の場所的構造）
　　　　
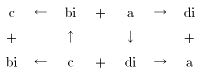
「止揚」の導入は次の表で表示できる。
「つながるかたち」（弁証法の過程的構造）
　
ひろがるかたち（場所的構造）の中央にあるbi +a とc+di は、つながるかたち（過程的構造）の２（混成）の上部（ａ＋ｂｉ）×（ｃ＋ｄｉ）に対応している。また、ひろがるかたち（場所的構造）の両側のａ＋ｄｉとｃ＋ｂｉ（縦に並んでいる第3の要素） は、２（混成）の下部（ａ＋ｄｉ）×（ｃ＋ｂｉ）に対応している。
混成の段階（ａ＋ｂｉ）×（ｃ＋ｄｉ）≒（ａ＋ｄｉ）×（ｃ＋ｂｉ）において、＝ではなく≒で表記しているは、この過程が純粋な論理的な過程ではなく、飛躍を含んでいるからである。≒は「およそ等しい」を表わす記号である。選ばれた２つの「論理的なもの」とは異なった関係性と指示性が形成されていること、また、新しい価値と意味が形成されていることを表わしている。混成モメント（ａ＋ｄｉ）×（ｃ＋ｂｉ）の後が、再び＝（等号）にもどるのは、この過程は論理的な過程だからである。ひろがるかたち（場所的構造）とつながるかたち（過程的構造）の混成の段階が弁証法の核心である。

過活動膀胱の改善

過活動膀胱の症状がこの2カ月ほど顕著になっていた。頻尿。基準は１日８回以上排尿らしいが、これに当てはまった。しかし、緑茶を静岡県人以上に飲むので回数はあまり気にしていなかった。尿意切迫感(急に排尿したくなる)と夜間頻尿(夜間に１回以上排尿に起きる)があった。夜中は1回起きるようになっていた。切迫性尿失禁(尿意がおこると、我慢できずにすぐに失禁してしまう)は微妙である。
過活動膀胱を改善する膀胱訓練がある。訓練といっても、これは尿意が起こってもとりあえず我慢してみるだけのことである。これを試みていた。自分では尿道を閉じているつもりなのだが、実際にトイレにいってみると下着が濡れているのである。ちびっているのである。これが切迫性尿失禁の範囲ならこの症状もあったことになる。
こんな症状が続くようなら困ったなあと思っていた。10日ほど休肝日を続けているが、しばらく前から夜間頻尿がなくなった。そして2日ほど前に尿意が起こって我慢するとき、我慢できて下着が濡れなくなっていることに気づいた。漏れていないのである。訓練が効いたのだろうか。改善していたらいいのだが。
2週間前はこんな感じだった。寝る前にトイレに行き、夜中に１回トイレに行く。朝起きてすぐトイレに行き、朝食後、昼までに２回。今日は朝起きてもトイレに行く必要がなかった。11時半にはじめてトイレに行った。次は14時半だった。次は17時半。最初は計りわすれたが、2回目の体重変化は約400グラム、3回目も約400グラム。今日の排尿は、回数も量も正常の範囲に収まるのではないかと思う。

庭に来る鳥

2階の窓からながめると目につくのはメジロである。みかん、びわ、はなもも、ゆすらうめのあいだを飛びまわっている。機敏な動きである。かきの実を啄みにくる鳥はスズメをはじめとしていろいろいるが、絵になるのはヒヨドリとムクドリである。食べる実があり、遊んだり憩える枝があり、わが家の庭は鳥に重宝がられているのではないだろうか。
「来る」をひらがなで「くる」と書くと朝永振一郎氏の庭になる（『庭にくる鳥』みすず書房1976年）。武蔵野の庭にきた鳥は次のようなものだった。
ひよどり、むくどり、おなが、しじゅうがら、あおじ、かわらひわ、ひたき、うぐいす、めじろ、きじばと、すずめ。
このなかで、おなが、あおじ、かわらひわはここでは見たことがない。図鑑で見るとおながは特徴的で見ればわかりそうである。わが家の庭には来ていないのではないかと思う。
他の鳥は来ている。朝永家には来なかったカラスもときどきみかける。またツグミも来る。
朝永氏は庭にえさ台を作りリンゴを置いていた。食べにきた鳥が残したふんのなかの植物の種を鉢にまいて育てていた。次のようなものが生えてきたとある。
ツタ、アオキ、ネズミモチ、イヌツゲ、ビナンカズラ、ナツメ、オモト、シュロ、ツルバラ。
「庭にくる鳥」は3ページほどの短いものだが、これが本の題名になったのは収録された随筆が「えさ台に残された鳥の糞からぽつりぽつりと出てきた木の芽みたいなところもあるなあ、と思った」ことにあった。

鳥の糞のなかの植物の種は条件が整えば発芽する。それは21世紀の尾張の庭でも同じである。クスノキ、クロガネモチ、ナンキンハゼ。これらは鳥がよそから運んできて野生えしたものである。トウジュロ、ビワは、もともと庭にあった木から運ばれたものだろう。気づいたときには発芽してから1,2年経っていただろう。いま、ビワは本家と比べると幹はまだ細いが背は高くなってしまった。

シジュウカラ

庭に出てみるとユスラウメの枝に白っぽい鳥が止まっていた。腹に黒いネクタイがあり、これがシジュウカラなのかと思った。これまでも来ていたと思うが、はじめて確認できた。撮影はできなかった。シジュウカラは四十雀と書くようだ。どうして「雀」?　「カラ」は鳥を表わす語だという。「シジュウ」は鳴き声に由来しているようだ。

休肝週

酒を飲まなくなって1週間たった。夜中に目が覚めなくなったことが大きい。これは単純に水分の取りすぎだったと思う。酒を飲まないと、肴にしていたチーズや刺身も食べたいとは思わない。飲まない、食べない。体重は７０キロを切った。読書の時間が増えたのもありがたい。禁酒は健康によい。そして、なにより財布によい。

長澤まさみと飛騨古川

「君の名は。」で市川悦子の声はわかった。しかし、長澤まさみの声はキャストの字幕が出るまでわからなかった。奥寺ミキ（瀧のアルバイト先の先輩）が長澤まさみの声だった。奥寺ミキは瀧といっしょに飛騨古川にくる。
長澤まさみは飛騨古川と縁がある。2002年のNHKドラマ「さくら」に主人公さくらの下宿先の「ろうそく店」の孫娘役で出演していた。高校生役である。飛彈弁で演じていた。