”夏休みの友”にピッタリの宿題〜ピタゴラスの定理とピタゴラ数

　｢女子高生の新しい証明｣に寄せられたコメントに､ピタゴラスの定理(3平方の定理)の4つの証明が紹介されていた。
　この定理は105通りの証明があるとされるが､大まかに確認すると､どれも似たり寄ったりと思えなくもない。
　勿論､中にはとても美しくシンプルな証明もあるし､複雑な公式や定義を使うものもある。例えば､(ピタゴラスが証明した様な)図形をパズルの様に組み合わせ､数式や計算を使わずに証明できるものや､トリッキーでややこしい証明を必要とするものまである。
　実際､三平方の定理の証明を105個全て解説したサイトがあるが､ここまで度が過ぎると何だかな〜に思えなくもないが､この定理の長い歴史を知るにつれ､過去の偉大なる数学者らを含め､人類が如何に真剣に取り組んできた定理であるかを理解できる。
　つまり､三角形(幾何学)と算術(整数論)の見事な融合が人類の誕生と共に存在してたかの様でもある。

ピタゴラスの定理と､その証明の歴史

　三平方の定理の歴史は､紀元前1800年頃のバビロニア(今のイラク南部)にまで遡るとされる。当時のバビロニアでは既に､今で言う”ピタゴラス数”(a²+b²=c²を満たす自然数の組(a,b,c))に関する数表が存在していた。
　5千年以上も前に高度な算術を扱う人類がいたとはこれまた驚きでもある。
　三平方の定理は”ピタゴラスの定理”とも呼ばれるが､古代ギリシャの数学者であるピタゴラス(BC569~BC500)は､バビロニア人がピタゴラス数を発見した頃から約1300年後の人なので､”ピタゴラスが発見した”という風評は誤りとされる。
　事実､(タレスの助言により)若き日のピタゴラスはバビロニアを旅し､三平方の定理を学んだという。彼はその定理をギリシャに持ち帰り､その証明を世界で初めて行った。が故に､この定理にピタゴラスの名が付く。

　そこでまずは､ピタゴラスの定理の様々な証明法を一部抜粋して紹介します。
　以下､｢三平方の定理の証明を16種類紹介！｣より大雑把にまとめます。

　最初に､ピタゴラス自身による証明ですが､これは数式を使わない中学生でも出来る証明です。が､”公式や定理がなぜ成り立つか？”という証明の概念を定例化したという点では､偉大な証明でもあります。
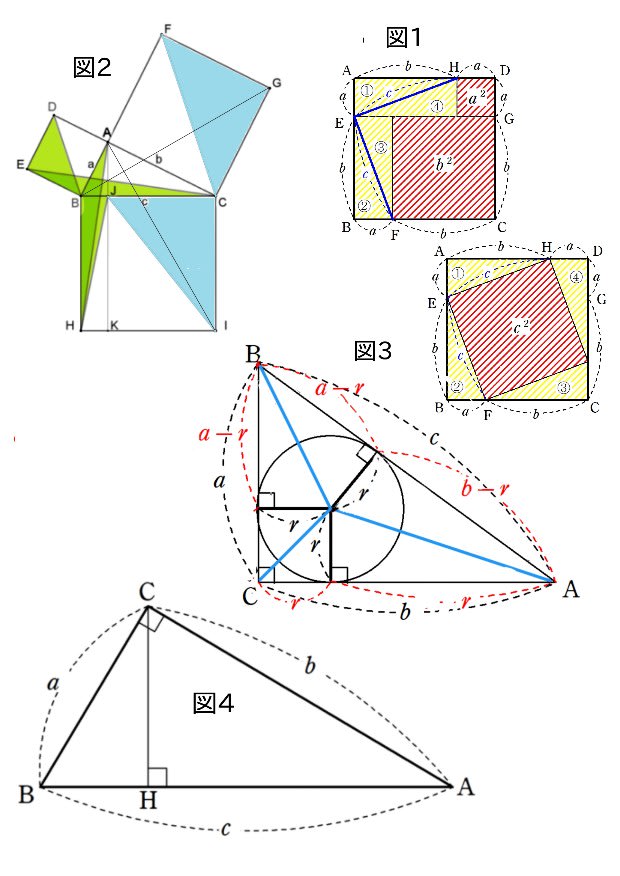
　まず､一辺がa+bの正方形にて､その内部に一辺がそれぞれa,bなる正方形を作る。図1(上イラスト)の様にE,H,F,Gをとり､EとH,EとFをそれぞれ結び､新たに出来た4つの直角三角形①②③④の斜辺をcとして､図のように回転移動させると､中央の正方形の面積はc²となる。
　これは正方形ABCDから4つの直角三角形を引いたもので､a²とb²の和になる。故に､a²+b²=c²が導ける。

　その後､ユークリッド(BC330~BC275)が続くんですが､紀元前300年頃に彼が書いた｢原論｣の中にある証明こそが”ピタゴラスの証明ブーム”に火を付けたとされます。
　よく知られる”花嫁の椅子”の図を使うんですが(図2)､等積変形や合同を用い(少し複雑になりますが)､青と緑で分けられた三角形の面積を比較すれば､証明は明らかですね。
　大まかに説明すると､まず△DEBに注目し､BE//CDから等積変形より△DEB=△CEBが言え､△CEB≡△HAB(合同)より△CEB≡△HABが言え､更に､BH//AK から等積変形を行うと△HAB=△HJBが言える。以上より､△DEB=△CEB=△HAB=△HJB=a²/2を得る。
　△FGCにても同様に考え､△FGC=△BGC=△IAC=△IJC=b²/2を得る。
　以上より､△DEB+△FGC=△HJB+△IJC=a²/2+b²/2=(正方形BHIC)/2=c²/2を得る(証明終)。
　これは､ピタゴラスのやり方を進化させ､幾何的要素のみを使うのが特徴でした。　

　モナリザで有名な画家､レオナルド･ダ･ビンチ(1452-1519)も､ユークリッドの”花嫁の椅子”に補助線を引き､合同な四角形を4つ作り､六角形の面積に着目するという一風変わった芸術的な証明でした。
　2つの合同な四角形からできる2つの六角形の面積が等しい事を示し､更に被ってる三角形を差し引けば正方形だけが残る事で三平方の定理を得る。
　ユークリッドの証明の別バージョンみたいですが､事実ダビンチは友人で数学者のルカ･パチョーリからユークリッドの証明を教わったとされます。個人的にはどうも好きになれない方法なので､詳細な説明は省きます。

大統領と女子高生とアインシュタイン

　補助線と言えば､1876年のジェームズ･ガーフィールド(後に第20代米国大統領)と､1938年の当時16歳のアン･コンディット嬢(米)の証明法が有名です。
　前者の場合､2つの直角三角形を補助線を引いて台形を作り､その台形の面積を2通りで表すというシンプルで単純な証明でしたが､数学者でもない45歳の政治家(それも大統領)が考案したという事で有名になりました。
　後者は､当時女子高生だったコンディットですが､”数学者が誰一人としてこれまでやったこなかった”とある様に､使われた補助線や全ての三角形が斜辺の中点から始まる様に､見事なまでに工夫されたものでした。
　これら奇抜な補助線により､三角形の面積を2通りで表して繋げるという証明の発見は多くの数学者を驚かせます。
　でも､個人的には(ダビンチ同様に)複雑すぎて好きではありませんが・・・

　私の一番のお気に入りが､1927年に出版された｢ピタゴラスの命題｣著者のイライシャ･スコット･ルーミスが発見したと主張する証明です。
　直角三角形の中に半径rの内接円を描き､(高校で学ぶ)”内心”の定義を使って証明します。
　これは図3から判る様に､⊿ABCの面積はab/2=(a+b+c)r/2で表せ､一方で長辺c=(a-r)+(b-r)で表せ､r=(a+b-c)/2となり､以上の2式を整理すれば､a²+b²=c²が簡単明瞭に示せる。これこそが美しくもシンプルで優雅な証明でもある(多分)。

　当時16歳だったアインシュタインの証明も(僅か1本の補助線だけの)相似性を使った､とてもシンプルなものでした(図4)。
　まず､⊿ABCにて頂点Cから辺cに垂線を下ろした点をHとし､三角形の相似(⊿BHC∽⊿BCA,⊿AHC∽⊿ACB)を使えば､BC²=BH×AB,AC²=AH×ABから､a²+b²=(BH+AH)c=c²が簡単に導けます。
　実際には､アインシュタインは3つの三角形の面積比を使ったんですが､(以下でも述べる)インドのパスカラが発見したとされる､線分比の方がずっとシンプルですね。
　但し､この線分比を使った方法は(そのシンプルさが故に)多くの書物に掲載され､実際にこれと似た様な証明がユークリッドの｢原論｣第6巻の命題31にある様に､ピタゴラスもこの方法を知ってたのではとの噂もある。

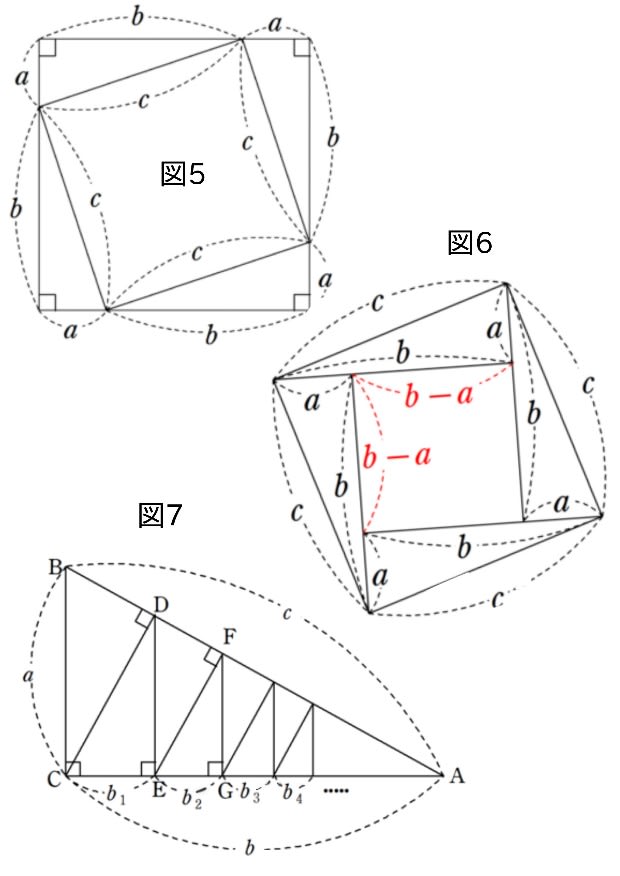
　教科書に最も多く登場するのが(ピタゴラスの証明にも使われた図と同じく)直角三角形4つと1つの正方形を組み合わせた正方形を作り､その面積を2通りの方法で表す事で三平方の定理を証明する(図5=下イラスト)。
　これは殆どの教科書で採用され､正方形の中に内接する正方形を組み入れる事で､直感的にも理解しやすい。
　一方でこれとよく似た証明には､(先にも述べた)中世インドの大数学者バスカラ(1114-1185)が､自著の中で示したとされる方法がある。
　直角三角形4つを組み合わせ､それらの内側に(囲まれる様にして)正方形を作り､その面積を2通りの方法で表す事で､これまた直感的に三平方の定理が導ける(図6=下イラスト)。
　因みに､この証明に関しては､古代中国の数学書｢周髀算経｣にも載っていた為､歴史としては中国の方が古い。
　ただ､パスカラの偉大な所は､負の平方根や無限大の操作を使いこなす､当時としては卓越した才能を持つ人物で､彼の著書は教科書としてインド全体に普及し､当時の優れたインドの数学を世界に魅せしめたとも言えます。

　最後に､｢女子高生の美しい証明｣で紹介した方法とよく似てるんですが､Facebookで数学記事を配信するJohnArioni(英､1948~)は相似性と無限等比級数を使って証明した。
　これは､⊿ABCの頂点Cから斜辺cへ垂線を下ろし､その直角からまた垂線を下ろし‥‥という事を無限に繰り返す事で三平方の定理を得る(図7)。 計算は少し複雑になるんですが､垂線によって辺bを無限に細かく分け､収束する無限等比数列の形に持っていくが故に､数学Ⅰ(三角関数)と数学Ⅲ(等比級数)とのコラボになってる。
　流石に20世紀後半にもなると､単純な証明方法は出尽くし､複雑でトリッキーな証明が目立ってきます。

　番外編ですが､トリッキーと言えば､ベトナムのBuiQuangTuan(1962~)によって考案された方法がある。これは､⊿ABCに外接する円と⊿ABCに繋がる2つの直角二等辺三角形を追加する事で､合同な三角形や垂心が誕生し､それらの性質を使って証明する。暇な人はやってみても損はないと思います。
　

最後に

　以上､他にも様々な証明方法が紹介されてますが､今日紹介した証明法は､中学生から高校低学年のレヴェルで理解出来るので､夏休みには丁度いい暇潰しになるのでは・・
　三平方の定理は直感である程度は判断できるので､特別な定義や小難しい公式を知らなくとも､様々なバリエーションの証明が可能になります。
　特に､内接円を使った証明は今に思えど､とても懐かしい思いがします。全てがシンプルに美しく流れるような証明で､我を忘れて机に向かってたもんです。
　三角関数がどうも苦手という人は､こういう所から入るとすんなりと受け入れれるかもですね。

　私が高校生の頃はネットとかは勿論､こうした溢れんばかりの数学の情報もなかったので､クソ真面目にテキストや問題集を睨めっこするしかなかったのですが､今はネット上にはあらゆる数学の教材に恵まれ､本人にやる気があれば(ですが)いくらでも勉強が出来ます。
　勿論､何でもそうですがやり過ぎれば､計算バカになるか？最悪キチガイになって人生を潰してしまうかもですが､数学の世界には様々な解法があり､人生と同じで､どれを選択し､どれを組み合わせるか､どこまでのめり込むかは個人の自由です。
　しかし､数学と同じく人生にも明確な答えはなく､答えがあったとしても探り出すのに一苦労します。ただ､その答えを探り出す過程こそが重要で､様々な発見やアイデアや創造を生み出してくれる。
　つまり､高度な思考を生み出すには一番てっとり早い。

　そういう意味でも､このバカ暑い時期に数学と戯れる事も悪くはないだろう。少なくとも高校野球や世界陸上を見て､肉体のみが躍動するカーニバルを楽しむよりかは､生存戦略や種の存続からしても有効に働くであろうか。
　というのも今や現代数学は､知が躍動する”思考のカーニバル”であるからだ。
　という事で､夏休みに一度は経験しておきたい､ピタゴラスのお話でした。

追記〜古代バビロニアとピタゴラス

　人生にはルールや法律があり､それらは人間が決めている。同じ様に､数学上のルールも基本的に人間(数学者)が決めています。
　なぜ？コンパスと定規で7角形が描けないのかは､こうした数学上のルールからはみ出すからに他ならない。
　人殺しや戦争と同じで､法律やルールに逸脱する事を世界規模で行えば､国家は破綻し､人類は最悪滅亡する。
　数学も同じで､窮屈で小難しい定理や厳格な公理に守られてるから､(非常に難しくはあるが)我々でも安心して扱える学問として存続している。難しければ難しい程に我々人類は､その数学の堅固性により守られている。

　一方で､数学は人工的に作られた言語の一種で､色んな所に人間が決めた都合が見え隠れする
　”なぜ？”とか”どうして？”とか疑問に思うのは頭の体操としては有効だが､AIは現実の問題を解く為の道具に過ぎない。AIでは数学の高度な概念はどんどん隠蔽されていく。むしろ隠蔽する為にAIが進化したのではないかとも思える。事実､AIチャットに”楕円関数と楕円曲線の違い”を問うても､チンプンカンな答えしか返ってこない。
　つまり､誰もわざわざ難しい事に頭を使いたくないのだ。
　多少の矛盾や不満があっても､AIがそれらを肩代わりしてくれるのなら､大いにやってもらおうというのが､人類と数学とAIの距離感のように思えてくる。

　私の様なアマチュア数学者は無責任なまでにこうした曖昧な考えを抱くが､現実に横たわるあらゆる事象を数学的に考える事で､それらの本質を最短距離で見つけ出す事は可能である。
　つまり､数学も我々を必要としてるし､我々も数学に守られている。
　ひょっとしたら今から5千年ほど昔の古代バビロニア人も､数学を人生の拠り所として生きてきたのかもしれないし､数学も人類とともに生き延びてきた。
　冒頭で書いた様に､紀元前1800年頃に書かれたとされる粘土板プリンプトン322には､ビロニア人が”三平方の定理を知っていた”事を示す数表が残っていた。
　つまり､整数論の起源が既に芽生えていたのである。

　中学生でも知っている”a²+b²=c²”という単純な定理だが､こうしたピタゴラス数の組(a,b,c)は無限に存在するが､何とバビロニア人は15組のピタゴラス数を発見していたのだ。それも､xy+((x−y)/2)²=((x+y)/2)²という恒等式と逆数表からx,yを求め､ピタゴラス数の組(a,b,c)を求めてたというから驚きである。
　事実､a=xy=1,b=(x−y)/2,c=(x+y)/2とすれば､a²+b²=c²は明らかで､逆数表から2つの数を選び､上式を満たすxとyを求め､ピタゴラス数(a,b,c)を求める事ができる。

　古代オリンピヤードや娯楽やカーニバルがなかった時代に既に彼らは､ピタゴラ数という数学のカーニバルを楽しんでいたのである。
　何という贅沢な知のイベントであった事だろう。そう思うだけで私の脳みそは弾けそうになるのだ。