1等の当選確率は”2000万分の1”という限りなくゼロの数字だが、我ら大衆はまるで当選したかの様な期待を抱き、宝くじを買ってしまう。
一方で、”夢を買うには安すぎる”とも言えるが、もし、AIの様に機械的で合理的な思考をもってれば、宝くじを買う人はいなくなる筈だ。
因みに、2018年の年末ジャンボ宝くじの1等当選確率は、0.00000005%だった。
人は物事が起こる確率を正確に認識してる訳ではない。つまり、”小さな確率ほど大きく見積り、大きな確率ほど小さく見積る”という”認知の歪み”を持って生きている。
宝くじが当たる確率などゼロに等しいにも関わらず、”ひょっとしたら・・”という過度な期待を寄せるのもそのせいなのだ。
誘惑に弱い私も、”ひょっとしたら可愛い娘が・・”と思いつつも、そんな確率は皆無に等しい筈なのに、夜の街に脚が向いてしまう。まるで、期待値という重力に惹きつけられるかのように・・・
そこで今日は、損得勘定で動く人の行動心理を関数により考察してみたい。
以下、「プロスペクト理論と行動経済学」より一部抜粋です。
プロスペクト理論とは、ダニエル・カーネマンとエイモス・トベルスキーが発表した行動経済学の理論(1979)で、価値関数と確立加重関数を理論の2つの柱とし、意思決定の場面で損得勘定がどう働くかを説明する。因みに、prospectとは”良い事が起きる見通し”との意味だ。
従来の経済学では”人は常に合理的な意思決定をする”事が前提で、理論と現実の間にズレが生じていた。一方でプロスペクト理論は、意思決定の不合理さを徹底的に観察し構築された、現実に即した理論とされる。
期待値とプロスペクト
そこで、意思決定における”不合理さ”を実例を挙げて説明する。
[例1]くじA=100%の確率で4000円もらえる。くじB=80%の確率で5000円もらえるが、20%の確率でハズレ。
これは、よほどの賭け好きでない限り、ハズレなしのくじAを選ぶのではないだろうか。しかし、期待値としてみれば両者とも4000×1=5000×0.8で、同じ4000円である。
つまり、確率論的には両者同じなのに、この不合理さを(笑ってしまいそうだが)従来の行動学では説明できなかったのだ。
今度は逆に、罰金を払うくじについて考える。[例2]くじA=100%の確率で罰金4000円を払う。くじB=80%の確率で罰金5000円を払うが、20%の確率で罰金なし。
こうなると人間の心理は変わり、期待値は同じ−4000円なのに、人は(罰金なしが含まれる)くじBを選びたがる。
この様に、私たちの意思決定は、確率や金額といった客観的数値だけから合理的に判断してるではなく、感情や感覚などのノイズ(歪み)に少なからぬ影響を受ける。
つまり、意思決定を歪ませる”ノイズ”こそが、プロスペクト理論の価値関数と確率加重関数となる。因みに、前者は”価値の感じ方の歪み”であり、後者は”確率の感じ方の歪み”となる。
私たちには”得をした嬉しさよりも、損をしたガッカリ感を強く感じる”という心理傾向がある。同じ5万円でも損した方がショックが大きいし、経済学者の筒井義郎氏らによると、損失がもたらす影響は利得の約2.25倍とされる。
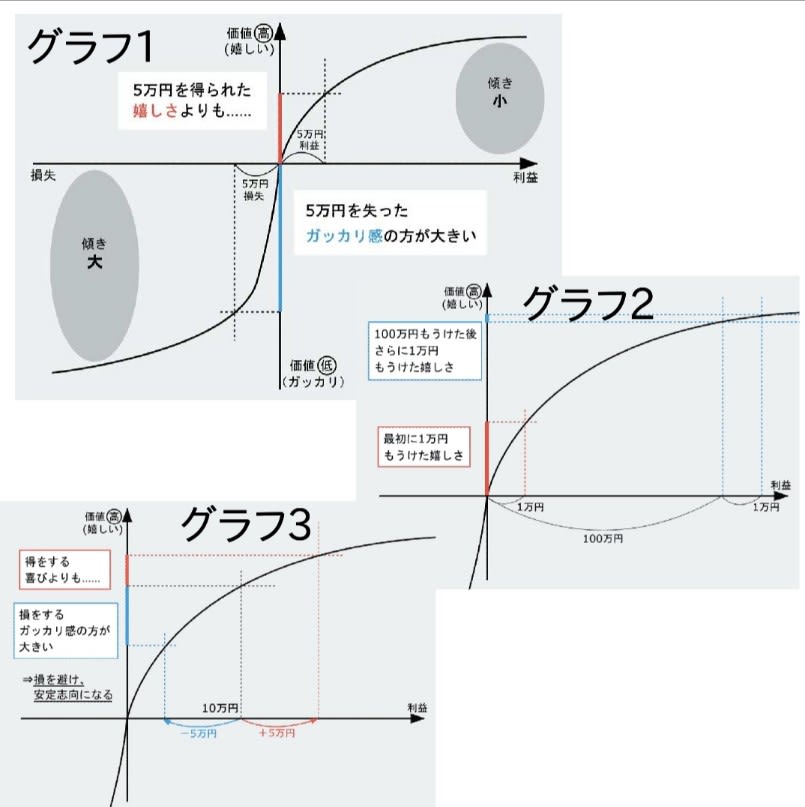
更に、損失のガッカリ感は金額に対して正比例ではない(グラフ1)。S字カーブを描く理由は”感応度逓減”にあり、利益・損失の額が大きくなっても、価値(喜びやガッカリ感)はあまり大きくならないとの心理現象にある。確かに、100万円勝った後で更に1万円勝っても、殆ど嬉しくはない(グラフ2)。
ギャンブルや投資の経験がある人は、勝ってる時ほど慎重になり、負けてる時ほど大博打に出たくなる傾向にある。が、冷静に考えれば、勝ってる時は余裕があり、大きな勝負に出る一方、負けてる時ほど慎重になるもんだが・・・
例えば、既に10万円勝ってる人は、更に5万円勝つ嬉しさより5万円負けた時のガッカリ感を強く感じる。故に、勝ってる時は負ける事を強く避ける傾向にある。反対に、10万円負けてる時は、更に5万円負けるガッカリ感より、5万円を取り返す喜びの方が大きくなる。つまり、負けるリスクを冒してでも大きな賭けに出る(グラフ3)。
関数はウソをつかない
まず1つ目の価値関数を使い、”くじ問題”について考えてみる。[例1]では、くじAとくじBの期待値は同じだったが、価値関数を使えば別の見方ができる。そこで、くじAの4000円もらった時の喜び(Joy)を4000Jとの単位で表すと、価値関数のグラフで見れば、くじBの5000円は4500J程にしかならない。
ここで”喜び”を期待値で表すと、くじA=4000J×1=4000Jで、くじB=4500J×0.8+4500J×0.2=3600Jとなり、喜びの期待値はAの方が上になり、人の心はAに傾く。
これは、[例2]でも同様で、損失のガッカリ感(Sad)の期待値(単位S)で表すと、くじA=4000Sで、くじB=3600Sとなり、ガッカリ値はAの方が上になり、人の心はガッカリ値の少ないBに動く。
こうして、損得勘定で動く心理を価値関数に置き換えると、人の意思決定の仕組みが理解しやすくなる。これはガロア理論でも同様で、解の仕組みを群の構造に置き換えると理解しやすい。
次に、2つ目の柱である確率加重関数だが、”高い確率は低く、低い確率は高く見積もる”という心理の歪み(偏り)をグラフ化にしたものだ。「行動経済学入門」によれば、確率加重関数では約40%が転換点となる。つまり、40%以下の確率は実際より高く、それ以上の確率は低く感じられる。結局、人は(悲しいかな)確率を客観的に理解してる訳ではない。
そこで今度は、冒頭の”くじ”を確率加重関数で説明する。
[例1]のくじBは”80%の確率で5000円がもらえ、20%の確率でハズレ”だったが、確率加重関数で言えば、”5000円がもらえる確率80%は実際より低く、ハズレの確率20%は高く”感じられる。故に、くじBの感覚上の期待値は、計算上の期待値4000円よりも低くなる。
一方、くじAの確率100%の時は、感覚のズレがないので、期待値は4000円のまま。従って、BよりAの期待値が高く感じられ、くじAを選びたくなる。
[例2]にても同様に、BよりAの罰金の期待値が高く評価され、逆にくじBが好まれる。
こうしたケースでは、価値関数と確率加重関数によるバイアスが2重に作用していたのだ。所詮は統計から導いた関数だから、当てはまらない人種もいるだろうが、知ってて損はないシンプルな理論ではある。
プロスペクト理論の応用
以上より、プロスペクト理論によれば、人は利得よりも損失を重く評価する傾向にある事が判るが、この損失回避性を応用したのが”フィア(恐怖)・アピール”である。
”この商品を買わないと損しますよ”と、顧客が被る損失をアピールし、購買意欲を高める交渉テクニックだが、例えば”この化粧品を使うと肌のハリが増します”と言うより、”この化粧品の成分が不足すると、肌のハリがなくなりますよ”と恐怖を植え付けた方が有効な宣伝になる。また、”数量限定”や”期間限定”も弱いフィア・アピールとも言える。
一方で、フィア・アピールとは反対に顧客の不安を取り除く事で購入を促す技術を”リスクリバーサル(リスク保証)"と呼ぶ。”買って損をしたら・・”という不信感が購入を妨げるケースも少なくない。つまり、返金や返品システムを充実させ、顧客を安心させる事が、売る事以上に重要な戦略となる。
プロスペクト理論を情報伝達に応用したのが”フレーミング効果”で、表現(フレーム)が違えば与える印象もガラリと変わる。
例えば、”90%の顧客が店舗Aのリピーターになる”と”10%の顧客が2度と店舗Aを利用しない”とでは、意味こそ同じだが、印象は全く違ってくる。
更に、”600人中200人が確実に救われる政策A”と”1/3の確率で600人全員が助かり、2/3の確率で誰も救われない政策B”では、言ってる事は同じでも、多くの人は”確実に救われる”の表現を含む政策Aを選ぶだろう。
また、質問の表現を反対にして、”600人中400人が確実に死ぬ政策A”と”1/3の確率で誰も死なずに済み、1/3の確率で600人全員が死亡する政策B”では少し迷うかもだが、”誰も死なずに”の表現を含む政策Bを選ぶのではないだろうか。
つまり、利益に関わる情報には”確実に・・”という表現が好まれ、逆に損失に関わる情報では”△%の確率で・・”というリスク表現が好まれる。
以上より、”利益を伝えるなら確実表現で、損失を伝えるならリスク表現”という簡単なルールを知っておくだけでも、有利に話を進める事が可能になる。
以上、STUDYHUCKERから長々とでした。
最後に
こうした高校で習う様な単純な関数でも、人の行動を予測するに十分なツールとなる。故に、人の意思決定を数値化し、関数に直せば、統計も確率も有効な手段になりうる。
勿論、人それぞれであり、特に今は多様性の時代であるから、こんな単純な関数に当てはまるケースも多くはないかもだが、結局は人なんて単純な生き物である。
悲しいかな、そういう私はもっと単純である。
クラブやスナックに返金システムというのがあれば、騙されたり誘惑に乗せられる事もないだろうが、夜の街は(私みたいな)人のいい無知な人種を騙す事で成り立っている。
つまり、期待値を限りなく膨らませ、顧客を店内に引き込み、逆に負債を膨らませる事で夜の街は生き延びる。”種の保存”と言えばそれまでだが、あまりにも出来すぎている。
近い将来、AIがこうした夜の街をハッキングし、店ごとの期待値を弾き出し、関数を使って顧客補正を加重し、我ら庶民にその最適解を提供してくれれば、誘惑という名の期待値による損失はずっと少なくなるであろうか。
つまり、損得ではなく期待値で動く我々愚かな人類は、確率と統計という単純な決断要素に支配される生き物なのかもしれない。
全米科学アカデミーは”数学的解決法を学ばなければ世界から取り残される”との危機感を打ち出した。更に、教育省は「数学により広がる将来」を発表し、数学の意義を訴えた。
日本は今、世界でも最低レベルの数学後進国にある。数学アジア選手権というのがあったら、最下位もありうるだろう。
政治家の知能は国民の知能に比例する。つまり、腐った脳では選挙も政治も国家も腐りはてる。数学を理解しろとまでは言わないが、少なくとも人の意思行動は数学に支配されてる事を知っておく必要がある。










誰かがコンナ不可解な言葉を世に問うたが
ヤッパりどうしても99匹に目が行くのは普通でしょう
過半数とか多数を尊重し重視する、それがコモンセンスと言うものでしょう
少数意見の尊重だなんてそれは所詮キレイ事にしか過ぎず、
多数決で世の中は回っているのが民主主義社会と言うものですよネ~
ただし1が自分にとって大切な唯一の存在なら話は変わって行くのでしょうが
自分の最愛の者とかだったらその他大勢は見捨ててもドウデモエエとか
最大多数の最大幸福なんて欲張るにも程がある噺です
まコンナ噺も確率的には希少なものとなるのかな
アインシュタインも分からない事は神の考える領域だナンて
エエ加減な事言って舌出しアッカンべ~ではアっカンやろ~
皆が目先の私欲だけを追い続けたら、自由主義と言えど世の中はパンクし、結局は格差社会である”最小数の最大幸福”に陥る。
これが民主主義と功利主義の限界で、そもそも幸福や苦痛を数字で表そうとする事自体矛盾してますが、仮に表せたとしても皆が功利を追求すれば、争いや戦争は必ず起きる。つまり、結果で見ればマイナスとなる。
更に、他者の不幸が自分の幸福になるというゼロサムの論理も働く。
こうした哲学上の矛盾を統計学的な視点で考察し関数を使い、正確な期待値を求めようとするのが数学であり、自分にとって何が本当の期待値になるのかを考える必要があると思います。
1人は世界の為にとか、世界は1人の為にとか、世界人類皆平和にとか、全体主義を彷彿させるカルト的狂言も未だに耳にしますね。
一方で、5/100億の確率の宝くじを買う事が幸福と考えるのなら、ベンサムにとってこれ程メデタイ事もないんですが・・・