”入試問題の正解は1つだが、人生には正解が幾つもある”
これは「ドラゴン桜」の桜木先生(阿部寛)の言葉だという事を、あるフォロワーの記事で知った。
”解が幾つもある”と聞いて、円周を等分する方程式であるxⁿ−1をふと思い出した。
数学の巨人ガウスに言わせると、xⁿ−1=0は円をn等分するからn個の解があると。
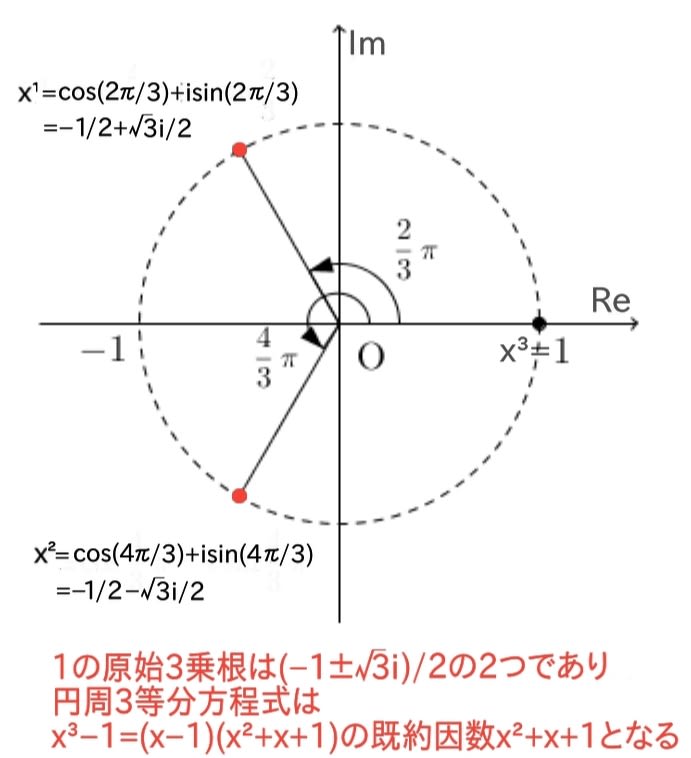
確かに、x²−1=(x−1)(x+1)=0は、x=±1で円を2等分し、x³−1=(x−1)(x²+x+1)=0は、x=1とx=(−1±√3i)/2で円を3等分する(上図)。
こうして見れば、人生の答えが我らの周りを等間隔に無数に並んでると思えば、人生も満更悪くはない気がする。しかし、人生も数学も思うほどに単純じゃない。
x⁴−1=(x²−1)(x²+1)=(x−1)(x+1)(x²+1)と分解できる所までは簡単だが、x⁵−1となると数学に慣れてる人以外は、x⁴+x³+x²+x+1が円を5等分する円分方程式だと一目で見抜くのは難しいだろう。
つまり、x⁵−1=(x−1)(x⁴+x³+x²+x+1)と分解できるからだ。もっと数学に慣れてる人なら、x⁴+x³+x²+x+1がそれ以上(因数)分解できない事を。そしてもっともっと慣れてる人は、アイゼンシュタインという数学者を思い出すだろう。彼が発見した”既約の法則”を使えば、これ以上因数分解できない事が判るからだ。
円周等分方程式の誕生
xⁿ−1を(整数係数の既約)因数分解した時に現れる、ある既約多項式を円周等分方程式(円分方程式)いう。
nが2以外の素数では、xⁿ−1=(x−1)(xⁿ⁻¹+xⁿ⁻²+・・・+x²+x+1)が成立し、既約因数xⁿ⁻¹+xⁿ⁻²+・・・+x²+x+1を円周等分多項式という。
ガウス的に言えば、xⁿ−1=0の事も”円の等分割を定める方程式”と呼ぶ。
xⁿ−1=0の解は、cos(2kπ/n)+isin(2kπ/n)、(k=1,2,…,n)と複素数根の形で表示されますが、(cosθ+isinθ)ⁿ=cos(nθ)+isin(nθ)というドモアブルの定理から即座に導き出せ、ガウス以前から知られてました。
円分方程式のn個の複素数根はn乗すると1(1のn乗根)になるが、これらのn個の根を複素平面(ガウス平面)上で表すと、単位円周上をn等分する点になり、それらを直線で結ぶと円に内接する正n角形ができる。故に、円周等分多項式と呼ぶ。
オイラー研究で有名な高瀬正仁サン的に言い換えると、正多角形の作図という幾何の問題は、円分方程式の根を求めるという代数方程式の問題に帰着する。また、根の実部と虚部はsin関数とcos関数の形で表示され、円関数である三角関数と円分方程式との関連も見て取れる。
更に、オイラーの公式(eⁱᶿ=cosθ+isinθ)を使えば、円分方程式の解はe^(2πik/n)で示される。
つまり、ガウスは円周等分方程式の解を複素指数関数の特殊値として表示した。しかしガウスの真意は数論にあり、円分方程式の解を用いて、平方剰余相互法則に結びつけます。
ガウスが創造した円周等分方程式論は実に不思議な理論で、異質な幾つもの側面が一同に共有されます。
複素変数関数論と代数方程式論と幾何の作図問題と数論が円周等分方程式の舞台で一堂に会し、密な関係で結ばれている。ガウスはそんな神秘的な光景を当り前の様に見る事のできる眼力の持ち主でした。
ベルヌイもオイラーもガウスも得体の知れない複素数に戸惑い、尻込みする数学者が多かった中で、何の躊躇もなく正面から堂々と複素数を語っていました。
彼らは人生に答えがなかったとしても堂々と人生を語り続けたでしょうね。
原始n乗根と円分方程式
上述したガウスの解の表示を使えば、1の3乗根は、cos(2kπ/3)+isin(2kπ/3)となり、k=1,2,3について計算した(−1+√3i)/2と(−1−√3i)/2と1の3つの根を繋ぐと正三角形になる(上図)。
そこで1のn乗根のうち、x=cos(2π/n)+isin(2π/n)のべきx¹,x²,x³,…を順につくれば、n乗して初めて1になるものがある。この様に、n乗して初めて1になる複素数を”1の原始n乗根”という。
例えば1の6乗根は、x¹=(1+√3i)/2、x²=(−1+√3i)/2、x³=−1、x⁴=(−1−√3i)/2、x⁵=(1−√3i)/2、x⁶=1の6つだが、{(−1±√3i)/2}³=1、(±1)²=1であるから、(−1±√3i)/2と±1の4つは、1の6乗根であっても原始6乗根ではない。
また、(1±√3i)/2は6乗して初めて1になるから1の原始6乗根である。つまり、6と互いに素な1と5のべき乗根となる。
故に、1のn乗根xᵏ=cos(2πk/n)+isin(2πk/n)が1の原始n乗根になる為の必要十分条件は、kとnが互いに素である事が解る。
1の原始6乗根x¹とx⁵は、x⁶−1=(x−1)(x+1)(x²+x+1)(x²−x+1)の既約因数x²−x+1の根であり、円周6等分方程式はx²−x+1となる。
同様に、1の原始3乗根は(−1±√3i)/2であり、円周3等分方程式はx³−1=(x−1)(x²+x+1)の既約因数x²+x+1となる。
実際に、xⁿ−1の因数分解をnが1から12までについてやってみる。
x²−1=(x−1)(x+1)
x³−1=(x−1)(x²+x+1)
x⁴−1=(x−1)(x+1)(x²+1)
x⁵−1=(x−1)(x⁴+x³+x²+x+1)
x⁶−1=(x−1)(x+1)(x²+x+1)(x²−x+1)
x⁷−1=(x−1)(x⁶+x⁵+x⁴+x³+x²+x+1)
x⁸−1=(x−1)(x+1)(x⁴+1)
x⁹−1=(x−1)(x²+x+1)(x⁶+x³+1)
x¹⁰−1=(x−1)(x+1)(x⁴+x³+x²+x+1)(x⁴−x³+x²−x+1)
x¹¹−1=(x−1)(x¹⁰+x⁹+x⁸+x⁷+x⁶+x⁵+x⁴+x³+x²+x+1)
x¹²−1=(x−1)(x+1)(x²+1)(x²−x+1)(x⁴−x²+1)
これを見れば判る様に、xⁿ−1の因数分解はnが大きくなるより、nの約数が多い程に分解される因子も多くなる。
但し、 係数が0か±1しか出てこない事に気付いた貴方は流石です。しかし、n=105の時に係数−2が登場し、n=385では絶対値3の項も登場。後はスパコンでの計算ですが、n=40755で絶対値100の係数が、n=40755では絶対値57から342が初めて登場する事が知られてます。
そこで、nの約数の数とxⁿ−1の因子の数を比較してみます。
n=2、約数の数=2、xⁿ−1の因子の数=2
n=3、約数の数=2、xⁿ−1の因子の数=2
n=4、約数の数=3、xⁿ−1の因子の数=3
n=5、約数の数=2、xⁿ−1の因子の数=2
n=6、約数の数=4、xⁿ−1の因子の数=4
n=7、約数の数=2、xⁿ−1の因子の数=2
n=8、約数の数=4、xⁿ−1の因子の数=4
n=9、約数の数=3、xⁿ−1の因子の数=3
n=10、約数の数=4、xⁿ−1の因子の数=4
n=11、約数の数=2、xⁿ−1の因子の数=2
n=12、約数の数=5、xⁿ−1の因子の数=5
見事に、nの約数の数=xⁿ−1の因子数となってますね。
そこでxⁿ−1を因数分解した時の最高次数を見てみますが、nが素数の時、n−1となってます。それに、nの約数が多い程少ない。
そこで、nと互いに素なn以下の自然数の数φ(n)と最高次数を比べます。
因みに、φ(n)はオイラーのφ関数で、”互いに素”とは、共通の約数が1だけ(最大公約数が1)で、例えばn=10の時の互いに素な自然数は1,3,7,9の4つとなる。すると
n=2、φ(2)=1、最高次数=1
n=3、φ(3)=2、最高次数=2
n=4、φ(4)=2、最高次数=2
n=5、φ(5)=4、最高次数=4
n=6、φ(6)=2、最高次数=2
n=7、φ(7)=6、最高次数=6
n=8、φ(8)=4、最高次数=4
n=9、φ(9)=6、最高次数=6
n=10、φ(10)=4、最高次数=4
n=11、φ(11)=10、最高次数=10
n=12、φ(12)=4、最高次数=4
つまり、xⁿ−1を因数分解した時の因子の数はnの約数と一致し、因子の最高次数はφ(n)である事が判る。この様に、xⁿ−1の因数分解とnの素因数分解は密に関わってますね。
xⁿ−1=0の解は勿論、n乗して1になりますが。上述した様に、この1のn乗根の中で”n乗して初めて1になる”ものを”原始n乗根”と呼びます。xⁿ−1=0の中で、”原始n乗根”のみを解とするものを円周等分方程式(円分多項式)といい、Φₙ(x)で示す。
n=12までの例で言えば、
Φ₁=x−1
Φ₂=(x²−1)/Φ₁=x+1
Φ₃=(x³−1)/Φ₁=x²+x+1
Φ₄=(x⁴−1)/Φ₁Φ₂=x²+1
Φ₅=(x⁵−1)/Φ₁=x⁴+x³+x²+x+1
Φ₆=(x⁶−1)/Φ₁Φ₂Φ₃=x²−x+1
Φ₇=(x⁷−1)/Φ₁=x⁶+x⁵+x⁴+x³+x²+x+1
Φ₈=(x⁸−1)/Φ₁Φ₂Φ₄=x⁴+1
Φ₉=(x⁹−1)/Φ₁Φ₃=x⁶+x³+1
Φ₁₀=(x¹⁰−1)/Φ₁Φ₂Φ₅=x⁴−x³+x²−x+1
Φ₁₁=(x¹¹−1)/Φ₁=x¹⁰+x⁹+x⁸+x⁷+x⁶+x⁵+x⁴+x³+x²+x+1
Φ₁₂=(x¹²−1)/Φ₁Φ₂Φ₃Φ₄Φ₆=x⁴−x²+1
そこで、nを奇素数p(2を除く素数)とする時、1の原始n乗根はφ(p)=p−1個ある。
一方、xᵖ−1=(x−1)(xᵖ⁻¹+xᵖ⁻²+・・・+x²+x+1)のxᵖ⁻¹+xᵖ⁻²+・・・+x²+x+1=0はp−1次式より、この解は全て1の原始n乗根である事が判る。
故に、Φₚ(x)=xᵖ⁻¹+xᵖ⁻²+・・・+x²+x+1となる。勿論これは、Φₙ(x)が既約(な多項式)であるという前提が必要ですが。
但し、既約である為には、アイゼンシュタインの(既約)判定法を使います。これは整数係数多項式がある3つの条件を満たせば既約になるというもので、定理自体は単純ですが、証明は難しいのでここでは省きます。
故に”既約”を前提とすれば、xⁿ−1の因数分解は簡単に導き出せます。
例えばn=10の時、10の約数は10,5,2,1の4つで、1の10乗根は1の原始10乗根と原始5乗根と原始2乗根と原始1乗根からなり、これらは重複しない。
つまり、x¹⁰−1=Φ₁Φ₂Φ₅Φ₁₀となる。k=1,2,5,10(10の約数)とすると、1の原始k乗根はφ(k)個あるので、上述した様にxⁿ−1の円分多項式の(最高)次数はφ(n)に等しいから、Φₖ(x)の次数はkである事が判る。
故に、x¹⁰−1=(x−1)(x+1)(x⁴+x³+x²+x+1)(x⁴−x³+x²−x+1)と因数分解できる。
これは、n=12でも同じで、12の約数は1,2,4,6,12より、x¹²−1=Φ₁Φ₂Φ₄Φ₆Φ₁₂=(x−1)(x+1)(x²+1)(x²−x+1)(x⁴−x²+1)となる。
つまり、何をいいたいのか?
これこそが、”約数さえ判れば円周等分多項式は簡単に解ける”という見事なトリックなんですね。
ガウスは何故、数学という難題塗れの人生を優雅に堂々と歩めたのか?
それは、難題の裏側に広がる雄大な背景を見抜く鋭い洞察眼と、数学という複雑多岐に組み合わさった魔術(トリック)とアイデアを併せ持ってたからでしょうか。
ガウスは数学の教授にはなりませんでした。もし彼が教授になってたら、”人生には正解が幾つもある様に思える。しかし、数学と同じで人生にも最適解というものは存在しない。だが、数学には人生と同じく無限の可能性がある。それに、その可能性の奥には美しい光景が広がってる”とでも言ったでしょうか。
ガウスの円周等分方程式を眺めてる内に、ふとそう思ってしまう自分がいる。










ガウスの凄い所は、この証明を代数的に解いたことでした。つまり、四則とルートだけで解き明かしてみせたのです。
そこでガウス青年は、とっさにx¹⁷−1=0という円分方程式を考え、x¹⁷−1=(x-1)(x¹⁶+x¹⁵+・・・x²+x+1)に因数分解し、x¹⁶+x¹⁵+・・・x²+x+1=0の16個の解(原始解)が自明な解(x=1)に加え、正17角形の頂点をなすことに気づきます。
x=1以外の16個の解を元とすれば、位数が17(素数)の巡回群をなし、対称性を持つことが分かります。その対象性を利用し、円分方程式の16の次数を下げ、2次方程式の組み合わせに帰着させて、解を導き出しました。
”17角形が2次方程式によって円内に描かれ得ることを発見した”とはこの事だったんです。
勿論、x¹⁷−1=0の解がcos(2πk/17)+isin(2πk/17)という答えを知ってればなんて事ないのですが。
要するにガウスは、
答えを知らなくても答えを導き出す術を神様から与えられてたんですね。
”何故、レムニスケートのn等分がn次ではなく、n²次の方程式が生ずるのか?”
この疑問を解く為に、ガウスはレムニスケート関数を複素関数として考察する一大決心をします。ここに複素関数論が芽生えたんですね。
その20年後、アーベルも同じ様な疑問から楕円関数を発見します。アーベルの”5次以上の方程式は代数的(四則とルートだけで)に解けない”の証明の背景には、彼の楕円積分に関する研究が横たわっていました。
というのも、四則とルートに加え、楕円積分(とテータ関数)を使う事で、5次方程式の解の公式を導き出せる。
つまり、若き日のガウスの夢はリーマンやアーベルらにしっかりと受け継がれ、現代数学の基盤を支え続けてるんですよ。
生きるとは夢を引き継ぐことかもしれませんね。コメント有り難うです。
円周等分多項式が<円周をn等分するn個の(複素)解を持つ>という代数的可解性はこれにより確定した。しかし、アーベルはある特殊な代数的可解方程式に関する論文で、このガウスの足取りの延長上に、アーベル方程式(楕円関数)の一般概念を発見する。
これこそがアーベルが楕円関数(楕円積分)の等分方程式の代数的可解条件のことで、この等分理論はガウスの<円周等分多項式は円関数のみならず楕円積分などの超越関数にも適用できる>(「整数論」第7章)が働いてる結果である。
つまり、アーベルはガウスの手法に倣い、代数的可解性を発見した。
ガロアもアーベルと同じ様に、既約方程式の代数的可解性をガロア理論の応用として導いていた。
ガロアが発見したとされる<全ての根が二個の有理関数として表記される>という「根の相互作用」は、実はアーベルがすでに論文で楕円関数の周期等分方程式の論文の中で述べていた。
事実、ガロアはアーベルの指摘を知っていたとされる。
ガウスからアーベル、そしてガロアに受け継がれた円周等分方程式。
人生の答えは継承することで無限に広がってるように思える。
転んだ君が言うように、答えの背後には大きな麦畑が広がってるんだ。
ガウスはもし円分方程式の次数がフェルマー数である2^(2ⁿ)+1の形の素数なら、円分方程式が平方根のみで解ける事を予想しました。
つまりガウスは、代数方程式の(代数的)可解性の基本的な条件を探り、と同時に可解性を否定する理論を追い求めたと思うんです。
ヤコビの楕円関数のモジュラ方程式(周期等分方程式)は代数的に可解ではないというアーベル予想は、ガロアの5次以上の方程式は代数的に可解ではないという”不可能の証明”に結びつき、大きな花を咲かせました。
因みにアーベル方程式とは、f(x)=0の係数域をkとする時、方程式のある解αを用いて、φ(α),φ(α),φ(α),・・・と表示され、かつφᵢφⱼ(α)=φⱼφᵢ(α)、j≠jという可換が成立する様な”k上の方程式”を言うんですかね(一応補足です)。
訂正です。
訂正です。
ルジャンドルは楕円関数の逆関数が積分の形をしてるので楕円積分と名付けたんですが、アーベルはそのまま楕円関数と呼んでたみたいです。
元々、楕円の孤長を表す式が積分の形をしてる事から、楕円積分と名が付いたんですね。
この逆関数が複素平面上では、2重周期を持つ三角関数である事を、ガウスやアーベルやヤコビが発見します。
楕円積分は楕円関数よりも先に研究されてましたから、混乱しますね。
今では、ガロア群の中でも”アーベル群(可換群)である様な方程式”という意味だけど、これはカミーユジョルダンが言ったもので、クロネッカーは巡回方程式を意味するものとして用いていた。
これはアーベルの言う”ある特殊な代数的可解方程式”そのものであり、ジョルダンの(単純)アーベル群とは区別する。
つまり、ジョルダンはガロアの立場から可解方程式を眺め、クロネッカーはアーベルよりから眺めたとも言える。
転んだ君が言ったk上の有理関数はk上の巡回方程式であり、アーベルは楕円関数の周期等分方程式の代数的可解条件の探求を通じ、アーベル方程式の概念に到達したんだ。
故に巡回方程式に可換が成立てば、k上のアーベル方程式になる。
結局、アーベルの楕円関数からアーベル方程式が誕生したと言っていいのかな。
結局、クロネッカーが言いたかったのは、”アーベル方程式は楕円関数に由来する”という事だったんですね。
楕円関数と言えば
普通はx²/a²+y²/b²=1を想像するわ
そうおもいません?