気象予報士試験の勉強では必ず登場する「オメガ方程式」。その姿は見る者を圧倒します。
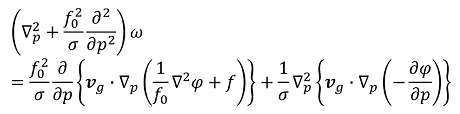
少し解りやすくするために、次の2つの式を適用すると
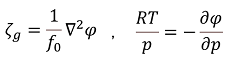
このように書き直すことができます。

鉛直運動(鉛直流の分布)は「渦度移流の鉛直シア」と「温度移流」によって生じる、という意味です。また、上の式には書いておりませんが、「非断熱効果」を加えることもあります。
数式自体が長く、複雑な形をしているので、その意味するイメージを描きにくいのが特徴です。試験対策としては、「鉛直流」の要因を考える際は「渦度移流の鉛直シア」「温度移流」あとは「非断熱効果」に着目する、と言うことを押さえておけばよいでしょう(実際、私がそうでした)。
この記事では、「ごく簡単な条件」を想定することで、この複雑・難解な「オメガ方程式」のイメージを読み解いていきます。
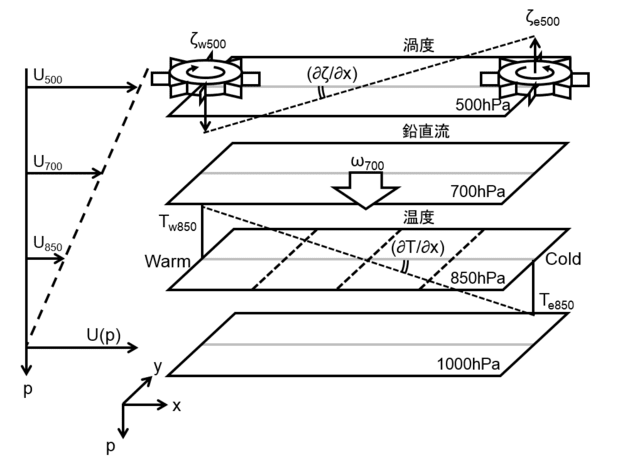
例えば、次のような場を考えてみましょう。x軸は東西方向、y軸は南北方向を表します。ここで、擾乱はy軸,p軸方向に一様とし、鉛直シアを持つ西風の一般流U(p)の場に重なるものと仮定します。
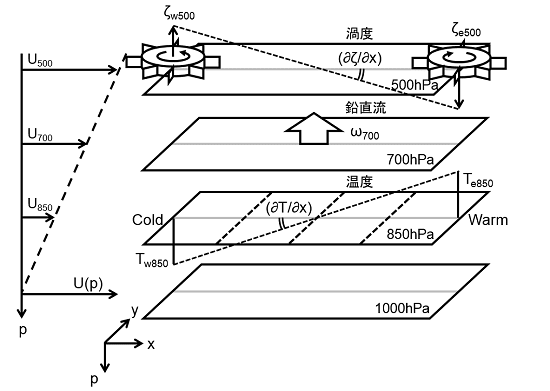
今回は4つの等圧面(500,700,850,1000hPa)に着目します。
想定する領域の長さをLxとし、500hPa面は渦度ζw500(西端)とζe500(東端)、700hPa面は鉛直流ω700(中央)、そして850hPa面は温度Tw850(西端)とTe850(東端)とします。また、一般流として等圧面毎にU500、U700、U850、U1000とします。これらは一様に西風とします(但し、上空ほど速度が増す)。
つまり、「500hPa面と1000hPa面の間の渦度移流の鉛直シア」および「850hPa面の温度移流」から「700hPa面の鉛直流」が決まることを考えています。FAX天気図のイメージです。
擾乱はy軸,p軸方向に一様と仮定したので、これらの物理量は「x軸方向のみ」を考えます。
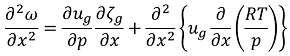
ここで、解ωの関数形について、次のような三角関数で表すことができると仮定します。
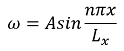
続いて、微分演算子、一般流の鉛直シア、1000hPa面の一般流を次のように近似します。
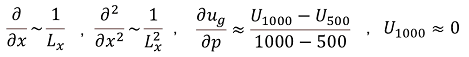
以上を「x軸方向のみ」のオメガ方程式に適用すると、次のような式が得られます。
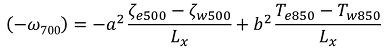
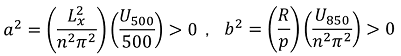
こうして簡単な代数方程式の形に帰着しました。あとは右辺の各項について見てみましょう。
右辺第1項について
・ζe500<ζw500 ⇒ (-ω700)>0 の側に作用する(上昇流)
・ζe500>ζw500 ⇒ (-ω700)<0 の側に作用する(下降流)
右辺第2項について
・Te850>Tw850 ⇒ (-ω700)>0 の側に作用する(上昇流)
・Te850<Tw850 ⇒ (-ω700)<0 の側に作用する(下降流)
このように、渦度や温度の「移流」が「傾き」の形で表現されるので、イメージがつかみやすくなります。
さて、上昇流となる場合のイメージ図は既出ですので、下降流となる場合のイメージ図も掲載しておきましょう。
ちなみに、Qベクトルを用いると、オメガ方程式は次のように書き表されます。

とってもシンプルになりました。
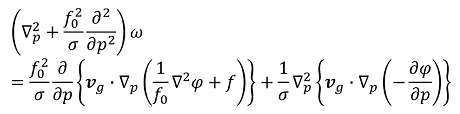
少し解りやすくするために、次の2つの式を適用すると
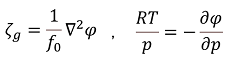
このように書き直すことができます。

鉛直運動(鉛直流の分布)は「渦度移流の鉛直シア」と「温度移流」によって生じる、という意味です。また、上の式には書いておりませんが、「非断熱効果」を加えることもあります。
数式自体が長く、複雑な形をしているので、その意味するイメージを描きにくいのが特徴です。試験対策としては、「鉛直流」の要因を考える際は「渦度移流の鉛直シア」「温度移流」あとは「非断熱効果」に着目する、と言うことを押さえておけばよいでしょう(実際、私がそうでした)。
この記事では、「ごく簡単な条件」を想定することで、この複雑・難解な「オメガ方程式」のイメージを読み解いていきます。
例えば、次のような場を考えてみましょう。x軸は東西方向、y軸は南北方向を表します。ここで、擾乱はy軸,p軸方向に一様とし、鉛直シアを持つ西風の一般流U(p)の場に重なるものと仮定します。

今回は4つの等圧面(500,700,850,1000hPa)に着目します。
想定する領域の長さをLxとし、500hPa面は渦度ζw500(西端)とζe500(東端)、700hPa面は鉛直流ω700(中央)、そして850hPa面は温度Tw850(西端)とTe850(東端)とします。また、一般流として等圧面毎にU500、U700、U850、U1000とします。これらは一様に西風とします(但し、上空ほど速度が増す)。
つまり、「500hPa面と1000hPa面の間の渦度移流の鉛直シア」および「850hPa面の温度移流」から「700hPa面の鉛直流」が決まることを考えています。FAX天気図のイメージです。
擾乱はy軸,p軸方向に一様と仮定したので、これらの物理量は「x軸方向のみ」を考えます。
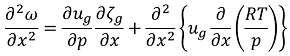
ここで、解ωの関数形について、次のような三角関数で表すことができると仮定します。
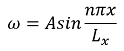
続いて、微分演算子、一般流の鉛直シア、1000hPa面の一般流を次のように近似します。
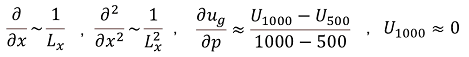
以上を「x軸方向のみ」のオメガ方程式に適用すると、次のような式が得られます。
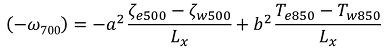
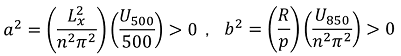
こうして簡単な代数方程式の形に帰着しました。あとは右辺の各項について見てみましょう。
右辺第1項について
・ζe500<ζw500 ⇒ (-ω700)>0 の側に作用する(上昇流)
・ζe500>ζw500 ⇒ (-ω700)<0 の側に作用する(下降流)
右辺第2項について
・Te850>Tw850 ⇒ (-ω700)>0 の側に作用する(上昇流)
・Te850<Tw850 ⇒ (-ω700)<0 の側に作用する(下降流)
このように、渦度や温度の「移流」が「傾き」の形で表現されるので、イメージがつかみやすくなります。
さて、上昇流となる場合のイメージ図は既出ですので、下降流となる場合のイメージ図も掲載しておきましょう。

ちなみに、Qベクトルを用いると、オメガ方程式は次のように書き表されます。

とってもシンプルになりました。

















