金のエンゼルで、おもちゃのカンヅメ当選！

写真は、チョコボールの金のエンゼル！

台風が来ていた9/18。
家族でイオンモール五条に行きました。
そこで妻が「テレビでおもちゃのカンヅメやってたん。欲しいし、これからチョコボール買っていくねん」と。
おかしコーナーで妻がチョコボールを4種類を1つずつ計4個しか取らないから、「そんなちょっとじゃ当たらんで」と僕がもっとカゴに入れようとしました。
すると「ええねん。ちょっとずつ買うねん」と。
「こら、もう諦めるパターンやな」と思っていました。

しかし、翌日仕事から帰宅すると「当たったでぇ～～～！」と。
見たら金のエンゼル！
一撃突破です！！！
初めて見ました。
たった4つで引き当てた、妻の運に脱帽・・・（笑）。
聞くところによると、金のエンゼルの出現率は1/1000だそうです。

すぐに応募したいところですが、金のエンゼルを職場でお披露目すると結構反響があり（笑）、結局送ったのは9/21でした。

そして待つこと、3週間・・・。
10/17に我が家に待望の「おもちゃのカンヅメ」が来ました！
今回はリニューアルされた、ニューバージョンです。

その外観がこちら。



そろそろこれより下は、中身のネタバレ注意です！　

高さは約20cmの黄金のキョロちゃん。
文字通り缶で出来ていますが、リニューアル後のはくちばしを触るとしゃべります。
くちばしを1回押すと、
・チョコボールの歌を歌う
・ジャンケンする
・早口言葉を言う
が順に再生されます。

また抱きしめるなど長押しすると、「大好き」とか、「ポカポカ」とか甘えてきます。

さて頭の蓋が開くので、それを開けると・・・



ご覧のようにおもちゃが入っています。
もちろん開封時は各々がビニールなどに包まれていますが、写真撮影時には取ってあります。
キョロちゃん缶の説明書や、おもちゃの説明書も付いています。

中のおもちゃを取り出すと・・・



左上は、「魔法のチョコボールボックス」。
箱が開け、写真右の黄色いキョロちゃんを入れて、箱の下のバーを引いて再度開けると、キョロちゃんがいなくなる。
要するに二重底の箱です（笑）。

左下は、「コロコロキョロちゃんゲーム」。
中央にある磁石の入ったキョロちゃんを、プレートを傾けて端の溝から中央の穴に入れるゲーム。

右上は、「キョロちゃんけん玉」。
もうそのまま、けん玉です（笑）。

右下は、「キョロちゃん定規」。
これもそのまま定規。
茶色の部分が180回転し、一直線維になります。

以上です。

子供の頃からの長年の謎がスッキリしました（笑）。

しかし今回のはおもちゃのカンヅメよりも、「金のエンゼルが出た」ことの方が希少なんでしょうね。
本当に妻の引きには、驚きました！

「京都のおすすめ」の総合索引へ

小5長男の作文（クロールのコーチ）

今日はちょっと脱線です（笑）。

昨日妻が「Kくん（長男）の学校の作文。見て。」と。
その全文が上記です。

まずは読んでみてください。
タイトルは「クロールのコーチ」です。

長男くんはやさしくて、年下の子の面倒もよくみるいい子です。
でもいい子過ぎて他人にもやさしく、自分にも甘いのか（笑）、競争などは得意ではないようです。
ちょっとヘタレなところもあってかわいいのですが、競争では仇になります。

その長男が頑張ったのがよく伝わってきます。
個人的には2か所。
試験の日、水がいつもより冷たく感じたという文学的表現（笑）。
そして最後のやっぱり背泳ぎは苦手というヘタレがこぼれた部分がお気に入りです（笑）。

実は水泳は幼稚園の年小時に、体験に連れて行きました。
そうしたら案の定、「やりたい！」って言いました。
そこで僕が「やりたいんだね。じゃあやってもいいから、お約束書いて」と言って、1枚約束を書かせました。
それが、「すいえいをしたいです。じぶんからやめるとはいいません。」です。
当然、文面のような事態に後々なることを想定してのことです（笑）。
妻は「幼稚園生にそんなこと書かせる？」と言いましたが、
僕は「じゃあ、なんのためにするの？」と返事しました。

小1の時、確かに妻から「Kくんが水泳、辞めたいって言ってる」と報告がありました。
即座に本人に事情を確認すると、やはりクロールがうまく出来ないから。
そこで「印籠」の登場。
「最初に約束したよね。自分から辞めるって言わないって。他の子が辞めようと、お母さんがいいと言っても、お父さんは許さない。出来ないからって、逃げてはいけない。」と言いました。
キビシかったようであるクロールのコーチにも感謝です。

最初に妻には言いましたが、正直水泳をさせたのも、泳げるようになるのは2番目の目的。
1番の目的は「つらいことでも逃げずに立ち向かって、克服すること」です。
結局小3の終わりで最後のクラスまで合格して、小4からの塾のため水泳は辞めました。

今から思えば長男は、小1で人生最初の「小さな山」は越えていたんですね。

そして今は受験という人生2つ目の「中ぐらいの山」を登っています。
彼なりにキビシイ目標を、自分で設定しました。
正直僕は登頂できなくてもいいと思っています。
「最後まで諦めずに登ろうとする経験」が、これからの彼の人生を支えると思っています。

このまま懸命に生きて、大人になって現れる「大きな山」を逃げず登れる人になって欲しいです。

「京都のおすすめ」の総合索引へ

2017 9/10のおでかけ報告2 最終（じき宮ざわ）

写真は、じき宮ざわ　3780円のコース

12:15に三条大橋のスタバを出てます。
河原町三条の金券ショップで、早速本日使用した市バスの1日乗車券2枚分を補充します（笑）。
河原町を下りってBAL、そして四条河原町の高島屋に入り、僕や妻の服をみます。

そして四条通を西へ歩きながら戻り、13:40に到着したのが四条堺町を少し上がったところにある「じき宮ざわ」さんです。
こちらは10席のカウンターだけのお店で、ランチは12:00～と13:45～の2回転のみ。
人気なので土日は2回転とも満席のことが多いようで、予約が必要ですね。

今回2日前の金曜日に、妻が「じき宮ざわで懐石のランチが食べたい」というので、すぐさま僕が予約しました（昨日書いたように妻はめんどくさがり屋なので、予約などは一切しません）。
そしたら「12:00～のお席は満席ですので、13:45～なら空いています」との返事。
それを聞いた妻は「13:45からかぁ～～。遅いなぁ」と・・・。

もう僕が言いたいこと分かりますよねぇ～～～！！！

彼女はいつも思いつきです。
事前に念入りに・・・
・・・デジャヴですね（笑）。

しかし合言葉は「多少の領空侵犯は撃ち落さない」！

実際に僕の口から出た言葉は、
「まあ、しゃあないんちゃう」です（笑）。

ランチは3500円、5000円、7000円のコースがあり、今回は1番お手軽な3500円の。
4の焼きごま豆腐が名物のようで、外はカリっと、中はふわっとしていて、とても美味しいです。
お釜で炊くご飯も、1膳目は表層のを少しだけ。
2膳目、3膳目とおかわりすると、お釜のより奥からよそって下さり、味わいが変わってきます。
とても美味しかったですが、じき宮ざわさんのお食事をより一層楽しむには5000円以上のにした方がいいのかなと思いました。

15:00頃に食事を終えて、市バス5系統で四条高倉から京都駅へ。
16:00に次男をお迎えして、妻と次男は先に帰宅。
僕は1人で時間をつぶし、18:00お迎えの長男を拾って帰宅しました。

「京都のおすすめ」の総合索引へ

2017 9/10のおでかけ報告1（スターバックスコーヒー 京都三条大橋店）

写真は、三条大橋 スターバックスの納涼床

日曜日の朝です。
実は土曜日の午後から長男と次男は泊りでアウトドアクラブに行っており、妻と2人でした。
なのでこの日は夕方のお迎えまで、2人でお出かけです。
大抵は大阪や神戸などに行くことが多いですが、暑さも和らいできたため珍しく京都市内です。

朝食後9:30に自宅を出て、市バスの1日乗車券を使って四条高倉へ。
僕の財布には常時市バスの1日乗車券が3枚入っています。
3枚である理由は、こうして妻と2人で使うことになっても1枚予備を残しておくためです（笑）。

10:00に大丸へ。
11:20頃まで妻の服や僕の服などをみます。

そして市バス5系統で四条高倉から河原町三条へ。
11:25頃にやって来たのが、三条大橋の北西にあるスターバックスコーヒー 京都三条大橋店です。
妻が「川床のあるスタバに行きたい！」と言うので、やって来ました。

川床が設営されるのは5月～9月まで。
しかもその期間も常時使用できるわけではなく、5月と9月は11:30～22:00、6月～8月は16:00～22:00です。
夏の昼は暑すぎますからね（笑）。

コーヒーを買って、開放された川床に出るや否や妻が、
「光が当たるし、中にしよう」と・・・。

そりゃ、そうでしょう。
川床は東向きだから、午前中は日が当たる。
川床のスタバにアナタが行きたいと言うのでわざわざ来たのに、ちゃんと事前に考えないから結局店内で・・・。
って、僕は思いながら、実際に僕の口にから出た言葉は、
「そうやな」・・・（笑）。

彼女はいつも思いつきです。
事前に念入りに計画したりはしないし、それどころかめんどくさがり屋なので自分で動くこともほぼなく、思いついた時点で僕に丸投げ。
でももうその辺を攻めたりはしません（笑）。

結婚5年目ぐらいまでは、お互いの不満をぶつけあってケンカしたりもしましたが、
もう恐らくですが向うも「分かり合い、解決することはない」と諦めたのでしょう、
お互いに「多少の領空侵犯は撃ち落さない」ようになりました（笑）。
前述のように、これ撃ち落とし合うと泥沼ですからね。
それだけは過去に学習しました（笑）。

それに撃ち落としてないのは、僕だけじゃないでしょうしね。
恐らく向こうも向うで、先々と計画して好き勝手する僕の自己中さに目をつぶっているハズなんで（笑）。

消して夫婦仲が悪いわけではない（こうして2人で出かけているぐらいですから）ですが、一瞬内心「はぁ！？」って思うことは時折あるわけです（笑）。

そんなこんなで、コーヒーを「屋内で」飲みながら（しつこい（笑）！？）、普段落ち着いて話せない日常のことなどを”仲良く”話しました。
12:15頃までゆっくりして、こちらを出ました。

「京都のおすすめ」の総合索引へ

長男くんの塾の問題6（算数 ただの図形の問題！？）

久々に長男くんの塾の算数の問題です。
今回、問題自体はそれほど難しくないです。
長男もやり方は分かっていました。
が、計算を間違えて不正解。

今回のポイントは、
これは確かに図形の問題ですが、
試験問題の中の1問とみた場合、
何の問題か、
ということでしょう。

興味のある方は、1度やてみて下さい。
本当に今回は、決して難問ではないです。


解答



上図のように、左の正方形は1辺12㎝、中央の正方形は15㎝、右の正方形は9㎝です。
なので、全体の面積は、
12×12＋15×15＋9×9＝144＋225＋81＝450。
この半分は225。
ウの下の欠けた部分は12×3＝36。

アイから下の長方形の面積は、225＋36＝261。
アイの長さは12+15+9＝36。
よってタテの1辺は、241÷36＝29/4。

最後に3cmを引くと、アウは29/4－3＝17/4

長男くんの解答用紙を見ても、そうやって解こうとしてます。
しかし残念ながら、計算を途中で間違えていました。
「惜しかったね。次は計算を間違えないようにしよう」で片づけるのは、普通の受験生。

さて今回はここからです。
受験の場合、「問題が解ければいい」だけではないでしょう。
算数も複数出題されるので、容易な問題は「早く正確に」解けると有利というか、志望校によってはそうしないと勝ち残れません。
そうした場合、有効なのが「先に答えまでの立式だけをして、計算は後でまとめてしてしまう」戦法です。

そうすることで、
・立式→計算→立式→計算と頭を切り替える必要がないので、劇的に勘違いや頭を切り替えるロスタイムが減る
・まとめて計算した方が、計算量も減る
のです。

具体的には、下のようになります。



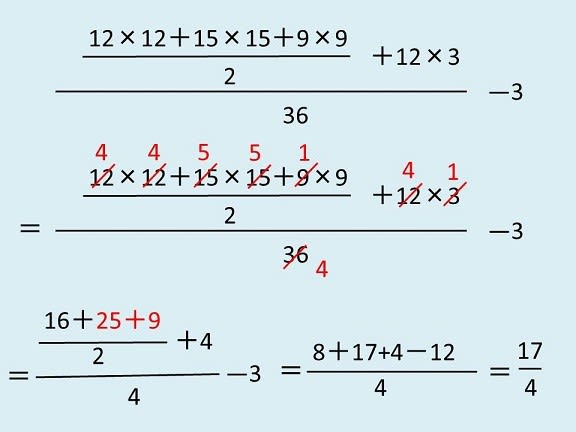
1列目が取りあえず答えまで立式だけしたものです。
あとは問題用紙をかなぐり捨てて、計算だけします（笑）。

その際に左手の大きな分数は、2列目のように各項9で割れ、36が約分出来ます。
すると3列目の左まで、式が簡単になります。
さらに赤い奇数同士を足してから2で割り、－3を分子に乗せると、中央のようになります。
よって17/4。

ご覧のように、この方法だと、
劇的に計算量や頭の切り替えが減るので、
計算間違いも減り、解答時間も短くなるんです。
まあこういうのが正に「受験テクニック」になるんでしょうね。
僕も「大学受験の時」は可能な限りこの方法で数学、物理、化学は解いていました。

しかし「小学生で」ここまでケア出来るのが、灘のレベルなんでしょうね（笑）。

「京都のおすすめ」の総合索引へ

2017 6/18のおでかけと近況報告

写真は、DEAN & DELUCAのローストビーフ重 1800円

今回は6/18のお出かけに加え、近況に少し触れます。

日曜日。
この日子供たちはアウトドアクラブでお出かけ。
僕が8:00に長男を京都駅へ車で送ります。
9:00に妻が次男を連れて京都駅へ。
送った後は妻と2人、車で八幡のコストコへ。
そもそも第2京阪道路と京奈和道をつなぐ八幡京田辺JCTが出来て、道の雰囲気が随分変わっていました。
9:40頃にコストコに着きましたが、やっぱり日曜日は人が多い（笑）。
12:00頃まで買い物して、一旦帰宅。

今度はバスで四条へ。
妻の希望で13:00頃に、烏丸蛸薬師にあるDEAN & DELUCAのイートインスペースで昼食。
僕は写真のローストビーフ重。妻は日替わりのようなプレートでした。
いつもは子供がいるので落ち着いて出来ない「子供関係以外の話題」を話しました（笑）。

食後はデパートへ。
大丸、高島屋やその間のお店へ。
僕も妻も買い物好き。
子供達がいるとこちらも落ち着かないし、3時間ぐらい楽勝で親がデパートから出て来ないのは男児2人にとっても拷問なので（笑）、
こういう機会に2人でゆっくりと観てまわりました。

そして17:00に子供達2人を京都駅で回収！？して、帰宅しました。

さて近況ですが、皆さんお気づきでしょう。
最近拝観予定が少ないです。
毎年6月は少なめにはなるのですが、今年は
6/4 亀岡 聖隣寺
6/10　粟田山荘にてお茶会
6/17　堀井七茗園に学ぶ宇治茶の今昔
の3日だけです。

と申しますのも、最近は長男関係のイベントが多いんです。
中学校の学校説明会、見学会、塾の保護者説明会など。
もちろん拝観の方の新たなネタがないということもありますが、そのリサーチ自体が以前より甘くなっているのも否定できません。

長男ももう5年生。
中学受験に取って5年生の夏以降は非常に大事。
国語、理科、社会は結果を出しているのでもう何も言っていませんが、苦手の算数はまだアドバイスが必要です。
こちらの興味自体がそちらに以降している部分も正直あります。

でもやりかけたことは途中で投げ出したくないので、
・新しいものには出来るだけ行って報告する（1度行ったところにもう1度行くことはまずないと思います）
・以前から蓄積している本編はすべて出し切る
のは続けて参ります。

もし本編も出し切り、新たな拝観報告もなくなった時は・・・もう潮時まもしれませんね・・・。

まあ今後もムリすることなく家族のおでかけなども交えながら続けて参りますので、今までよりはユルイ気持ちで読んで頂ければと思います。

「京都のおすすめ」の総合索引へ

長男くんの塾の問題5（算数 図形2）

昨日に引き続き2問目です。
こっちの方が昨日のより難しいと思います。

問題設定は非常にシンプルですが、容易には解けません。
非常にいい問題だと思います。

興味のある方は、チャレンジしてみて下さい。

解答
まず∠AEB＝68°、∠AFD＝67°、∠EAF＝45°は、すぐに書くでしょう。
そこで、んっ？∠EAF＝45°！
てなりますよね。
直角二等辺三角形が気になります。
そこでFからAEに垂線を引いてみたりしますが・・・解けないです。
確かに45°は気になる数字ですが、これでは正方形＝4つの辺の長さが等しいという情報が有効利用できていません。

さて、どうしよう。

そこで23°と22°を足せば45°・・・可視化したいな・・・と思えるかがポイントですね。
22°と23°を目に見えるようにくっつけるのですが、その際に正方形→AB＝ADを利用して、
三角形ADFをABにくっ付けて45°を作り三角形ABGとすると、図2のようになります。



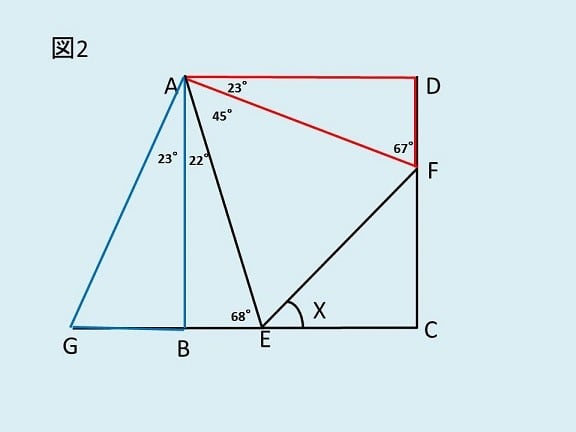
すると∠GAE＝45°、三角形ABGと三角形ADFは合同なので、AG＝AF。
∠FAEも45°・・・。
これらを比べると、AEは共通しているため2辺とその間の角度が等しいので、図3のように三角形AEGと三角形AEFは合同です。



三角形AEGと三角形AEFは合同なので、∠FEA＝∠GEA＝68°。
よって
∠CEF＝180－68×2＝44°
です。

この解法を教えると、長男は「なぜそのような補助線を引くことを思いついたのか？」と聞かれました。
そうですよね。
僕も子供の頃は「こんなん思いつくかっ！」って思ってました。
けれど数多くの問題のポイントを意識しながら解法の経験を積むと、必然的に出来るようになるんですよね。
究極のパターン認識。
ほとんどゲーマーと同じですね（笑）。

今回のポイントは具体的には、
45°という角度を可視化しようと思えるか、
またそうすることで正方形という条件も同時に有効活用できる、
ことですね。

「そこに気づけるような経験を積む」、いわゆる「図形センスを磨く」ための問題です。

「京都のおすすめ」の総合索引へ

長男くんの塾の問題4（算数 図形1）

小学校5年生の長男ですが、最近は国語、理科、社会は塾の模試でも一定の結果をコンスタントに出しているので、もう本人に任せています。
しかし算数は苦手なようで、まだまでですね（笑）。
今回もハイクラスの講座の問題が分からず、質問してきました。
解答にやり方が書いておらず、答えの数しか書いてないのです。
まあやり方は「自分で考えろ」ということなのでしょう。

今回は2問あり、まず1問目が上です。
結構スタンダードな問題ですが、ハードルが2段階あります。

興味のある方は、考えてみて下さい。


解答
普通台形の面積といえば、（上底＋下底｝×高さ÷2ですが、今回はいずれの長さも分からないですね。
このように面積が公式で直接でない場合、解法は2つ。
1：より大きな図形から一部を引くことで、残りの面積として出す。
2：等積の別の形に置き換えて求める
のが定石でしょう。

今回は全体の形をみれば、1はキビシそうです。
なので2で攻めてみます。

問題に戻ります。
まず問題になるのは、中点Eの処理でしょう。
Eは弧BCの中点ですので、FはCDの中点などではない。
Eの使い方は、図2のようにAEを結んだ補助線を使うしかないのは、図形問題の経験を積めばわかります。
すると馴染みのある30°、60°の直角三角形が見えてきます。



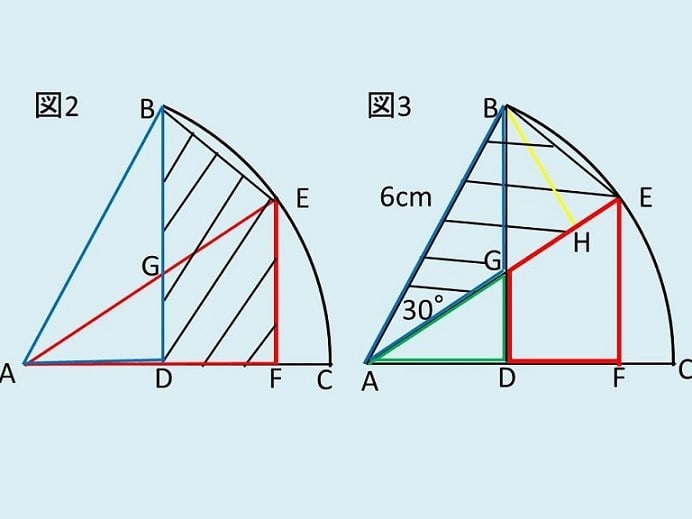
つまり図2の三角形AEFと三角形ABDは、斜辺が6cmの30°、60°の直角三角形なので合同であると分かります。
すると図3のように両者から三角形ADGを引いた、三角形ABGと台形DFEGの面積が同じです。

以上より
求めるべき台形BDFE＝三角形BGE＋台形DFEG
求めるべき台形BDFE＝三角形BGE＋三角形ABG
求めるべき台形BDFE＝三角形ABE
となります。

ここまでが1段階。

三角形ABEは6cmの2辺の内角が30°の三角形。
BからAEに垂線を降ろせば、三角形ABHは30°、60°の直角三角形なので、BHは3cm。
よって、
台形BDFE＝三角形ABE＝6(AE)×3(BH)÷2＝9㎠
となります。

・中点Eを正しく使えるか、
・60°があれば、30°90°の直角三角形を見出せるか、
が、解答のポイントですね。

「京都のおすすめ」の総合索引へ

長男くんの塾の問題3（理科 月の満ち欠けの周期の概算）

小学校5年生の長男くんの塾の問題の第3弾です。
今回は理科。
こういう結果は知っているけど・・・みたいな内容の裏付け問題って面白いですね。
まあ概算ではありますが・・・。

興味ある方は、順番に解いてみて下さい。
①～③までは大したことはないでしょう。
問題は④です。

解答
①　これはいいでしょう。
360日で360°ですので、1日1°です。

②　27日間の地球の公転ですので、1°×27日＝27°ですね。

③　これもいいでしょう。
27日で360°ですので、
360÷27＝13.33　　　　　　約13°です。

④　さてこれです。
ここまでの情報を図を使って整理します。



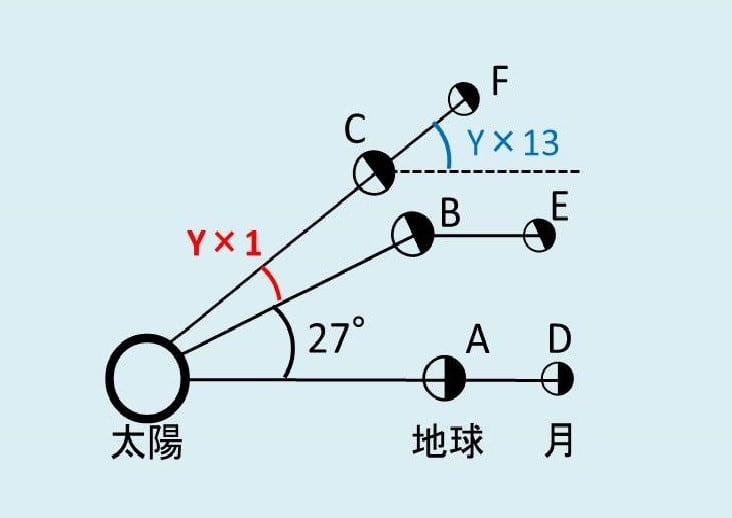
月が地球のまわりを1周したBまでは27日ですので、黒の角度Xは27°でした。
ここからさらにY日後に再度Aと同じようにCで満月になるとします。
すると赤の角度はY日の地球の公転ですので、Y×1°＝Y°
また、
青の角度はEからFへのY日での月の公転ですので、Y×13°=13Y°です。

そしてここからは算数の図形。
黒の角度と赤の角度の和は、1番下の黒線と点線が平行なので、同位角で青の角度と同じになります。
よって、
13Y=Y+27
12Y=27
Y=2.25

月が地球を1周してからさらに2.25日後ですので、
27+2.25=29.25日
ということで、最も近いのはエの29.5日になります。

どうでしょうか。
ウチの長男くんは案の定、④が分からず。
理科やってるのに、同位角？みたいな（笑）。
まだまだひよっこです。

なんとなく月の満ち欠けは30日弱って知っていますが、こうして考えてみるとなんだか少し分かったような気がしますね（笑）。

「京都のおすすめ」の総合索引へ

2017 5/5のお出かけ報告（吹田スタジアム J1リーグ ガンバ大阪VS清水エスパルス）

写真は、試合中のフィールドを指定席から

スミマセン。
GWネタなんで、家族関係しかも今回は大阪です。

さて昨年の秋のこと。
プロ野球の日本シリーズをテレビで観ていたら、次男が「僕、野球観に行きたい！」と言い出しました。
すると長男が「僕は野球よりサッカーがいい」と。
それなら「来シーズン、サッカーと野球の両方に連れて行ってやる」と約束しました。
どうせサッカーを観るならJ1ということで（パープルサンガ、ゴメン）、新春早々にガンバ大阪日程を確認しました。
土曜日は塾があるからダメ、日曜日でアウトドアクラブと模試がない日。
しかも試合開始が18:00とかは帰宅が遅くなるから、妻NG。
いろいろな制約を考えると、もう候補は5/5ぐらいしかありませんでした。
野球は7月のチケットを確保しました（笑）。

8:45に自宅を出発。
地下鉄で四条駅→阪急電車で烏丸～茨木駅～南茨木駅→モノレールで南茨木駅～万博公園駅へ。
もうモノレールの南茨木駅あたりからエライ人出でした。

10:00に到着。
改札を出て、スロープを降りた正面が”ららぽーと”や、水族館のニフレル。
左手の歩道橋を渡ると自然文化園（太陽の塔がある公園）。
右手の階段から”ららぽーと”の背後に回り込むと吹田スタジアムがあります。

14:03キックオフですが、もうガンバのユニホーム着た人が多数。
まず妻は1人で、ららぽーとへ。
僕と子供たちは自然文化園へ。
公園の遊具で遊びます。
11:15頃には飽きと暑さで撤退（笑）。
妻と合流して、吹田スタジアムへ向かいます。

前述のように右手から”ららぽーと”を回り込んで吹田スタジアムへ向かいますが、これが結構遠いです（笑）。
11:50頃、スタジアムに到着。
今回はメイン側1階の1番後の指定席（1人4500円）。
両サイドのゴール裏は熱狂的なサポーターがいっぱい。
こちらは自由席なので早くから来られるんですね。
ウチは子供連れのゆるい観戦なので、指定席で十分です（笑）。
相撲で例えると、東西側は自由席でマジのサポーターが来てる。
正面と向正面はゆっくり観る指定席といった感じです（笑）。

今回のチケットは職場の熱心なガンバサポーターさんにウチの事情を説明したら、家族でゆっくり観られる席を確保して下さいました。
上記以外の注意点は、向正面側！？は時間が経つほど直射日光が当たって暑いです。

そしてこんなにも早く来たのは、スタジアムグルメです。


席までの広い廊下をぐるっと1周、写真のように大阪のお店がたくさん出店されています。
これを昼食にするのです。
今回は焼肉たむらの焼肉弁当、牛串、なにわ鉄板焼き 門左衛門のたこやき焼きそばなどを頂きました。
11:50頃なら待っても5人ぐらい。
12:30頃になると15人待ちぐらい。
13:15頃になると30人以上待ちぐらいになります。

スタジアムの1周あるのですが、ガンバゴール裏の1辺は清水サポーターが、清水ゴール裏の1辺はガンバサポーターの出入りが禁止です。
ユニフォームを着ていなければ、そういう制約はありません。



そして13:30頃から応援合戦が始まり、俄然盛り上がってきます。
長男、次男も3万人の大声援なんか聞いたことがないので、圧倒されていました（笑）。

14:03いよいよキックオフ。
前半決定的なチャンスが2回ほどあるも、決めきれず・・・。
やや押され気味に0-0で終了。
しかし試合中、相撲でいう東の花道のところでチアガールさんがずっと踊ってるんですが、あれって意味あるのかなぁ。
メインから以外はほとんど見えないし（笑）。

15分のハーフタイム。
15:03、後半キックオフ。
後半早々に清水がゴール・・・。
スタジアムの8割がし～～～ん。
2割のオレンジの一角が大熱狂。

すぐにガンバは7番、遠藤保仁（ヤットさん）投入。
すると直後にガンバ、同点ゴ～～～～～ル！
今度はスタンドの8割が大熱狂！！！

後はやや押され気味に、ドローで終了。
スタジアムを15:53頃に出ました。

帰りは電車の乗り継ぎがスムーズで、17:20には帰宅しました。

ゴールした時の熱狂も、された時の”し～～～ん”も経験出来たので、子供達も楽しかったようでいい「こどもの日」になりました。

「京都のおすすめ」の総合索引へ

長男くんの塾の算数の問題2（カードを繰ると・・・）

　
またまた暇つぶしです（笑）。
先日小5の長男くんから「これが出来ない」と質問されました。
解答には答えしか書いていないので、やり方が不明と。

要するにカードを繰る問題です。
1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20
が、1回の操作後には、
1、11、2、12、3、13、4、14、5、15、6、16、7、17、8、18、9、19、10、20
になるということです。

お時間がある方は、まず考えてみて下さい。

解答
まあ3回ぐらいなら全部書いても出来そうですが、結構イライラします（笑）。
しかし②はそうもいかないので、根本的に解決しておきましょう。

まずこういう数列は、必ず何らかの法則があります。
でないと②は解けません。

ではどういう法則があるのか。
ポイントは
カード全体の動き追うのではなく、
各カードが「何番目かだけを追う」
ことです。

まずカードを2つに分けて交互に混ぜるのですから、
1番目～10番目のカードは同じ法則、
11番目～20番目のカードは同じ法則で
次の運命が決まるのはいいでしょうか。

では1番目～10番目のカードは次どうなるのか。
1→1、2→3、3→5、4→7・・・。
基本的に後ろに必ず1枚入ってくるので、n番目のカードは次は
n×2-1番目
になります。

では11番目～20番目のカードはどうなるのか。
11→2、12→4、13→6、14→8・・・。
10番目から前を切り捨てた順位で、前群のカードの後ろに付いていくので、n番目のカードは次は
　（n-10）×2番目　
になります。

これで①は終わりですね。

①
1回目終了時は、8が赤の法則で　8×2-1＝15番目
2回目終了時は、15が青の法則で　（15-10）×2＝10番目
3回目終了時は、10が赤の法則で　10×2-1＝19番目です。

②
さて2000回と来ました。
これはもう何らかのサイクルがあると踏むしかないです。
でないと解けないので（笑）。

そこで、
1回目終了時は、13が青の法則で　（13-10）×2＝6番目
2回目終了時は、6が赤の法則で　6×2-1＝11番目
3回目終了時は、11が青の法則で　（11-10）×2＝2番目
4回目終了時は、2が赤の法則で　2×2-1＝3番目
5回目終了時は、3が赤の法則で　3×2-1＝5番目
6回目終了時は、5が赤の法則で　5×2-1＝9番目
7回目終了時は、9が赤の法則で　9×2-1＝17番目
8回目終了時は、17が青の法則で　（17-10）×2＝14番目
9回目終了時は、14が青の法則で　（14-10）×2＝8番目
10回目終了時は、8が赤の法則で　8×2-1＝15番目
11回目終了時は、15が青の法則で　（15-10）×2＝10番目
12回目終了時は、10が赤の法則で　10×2-1＝19番目
13回目終了時は、19が青の法則で　（19-10）×2＝18番目
14回目終了時は、18が青の法則で　（18-10）×2＝16番目
15回目終了時は、16が青の法則で　（16-10）×2＝12番目
16回目終了時は、12が青の法則で　（12-10）×2＝4番目
17回目終了時は、4が赤の法則で　4×2-1＝7番目
18回目終了時は、7が赤の法則で　7×2-1＝13番目

やっと決着がつきました。
というのも、13が13番目なので、元に戻ったということです。
19回目以降は、1回目以降と同じことの繰り返しです。

ですから、
2000÷18＝111・・・2
あまり2なので、2回目終了時と同じということで11番目です。

うちの長男はまだまだですが、小5でこれが解けるって大したものですね。

「京都のおすすめ」の総合索引へ

長男が塾で習った算数の公式が意味深（笑）。

連休の朝からひまつぶしです（笑）。

長男は今小4の3月。
某進学塾に通っており、そちらは2月から新学期なので5年生です。

一応子供の宿題の問題とノートは、どのようにしてやっているか毎回見ています。
怪しそうなのがあったら、質問したりします。
その中に上ような解法がありました。
長男に「これどうやって解いたん？」と聞くと、
「塾で習った公式で解いた」と。

「いやいや公式なんて、その意味が分からないと使えないよ」ということで、長男に公式の意味を聞くと分からないと。
しかも塾でも公式の内容について言及はなかったと。

そこでこの公式の意味を考えたのですが、それがチョー意味深なんです（笑）。

まず、
立候補者の4人をA、B、C、D、当選者をA、Bと仮定します。
このAとBが最も均等な票数でギリギリ当選する場合を考えると、
A10票　B10票　C9票　D9票
でしょう。

しかし10票では当確になりません。
というのも、野党相乗り候補のように、Dの支援者がCに投票すると
A10票　B10票　C18票　D0票
でCが当選になるからです。

と、いうことは、AとBがコワいのは、「多数の候補者」じゃなくて、「強力な1人のライバル」だということです。

そこで賢いAとBは考えるんです。
その「強力なライバルが独走しないようにコントロールしよう」と。
まずAとBは誘います、Cを。
「一緒に当選しようぜ！」って。

まずは「3人で山分けだ」ということで、3で割る。
これが公式の（当選者数＋1）で割るの意味。
これには
・Cを独走させず、同票におさえる
・D（もしくはそれ以外のすべて）を確実にレースから降りさせる
という2つの意味があります。

3で割ると1人12票ずつ・・・・で、2票余る。
その余った瞬間、AとBは自分を当確にすべく最後の1票ずつを目にもとまらぬ早さで奪うのです！
これが最後の+1。
そしてAとBは目論見通り、ギリギリですが確実に当選するという寸法です（笑）。

どうですか。
なかなかえげつないでしょう（笑）。

しかしまだこれは2票余ったからいいようなもの。
もし総投票数が36票だったら、A12票、B12票、C12票。
と、3人で仲良く分けたハズなのに、AとBが突然Cから1票ずつ「横取りして」、A13票、B13票で当選、C10票で落選ってことですからね・・・。

こんなの「手をつないでみんなでゴール」とか言ってる学校じゃ教えられっこないです（笑）。

そして最後に、この式の意味。
長男に・・・教えましたよ。
聞いてニヤって笑ってました。
子供にこういうことをする大人になって欲しくはないですが、こういう罠もあるってことは親が教えるしかないんでしょうね（笑）。

「京都のおすすめ」の総合索引へ

2017 謹賀新年

明けまして、おめでとうございます。

ブログの掲載は未だ紅葉真っ盛りですが、当面は遅れたままで掲載します。
冬は拝観場所が減ってくるので、いつものようにそのうち追いつくと思います。

追いついたら、今後は溜まった本編を掲載します。
そうしているうちに春になるので、また拝観報告が並ぶと思われます。

まあこんな感じで今年もやって参ります。


さて昨年の4/10に「別の画を抑えに来た」と言っていたのは、今回の写真のことです。

こんなところに鶏の石像があるとは、なかなか気づかないですよね。
冬来たりなば、春遠からじ。
冬の旅が終わったら、あっという間にまた春です。

なお本日は22:00にも更新があります。

「京都のおすすめ」の総合索引へ

謹賀新年

上にもあるように、そろそろ本編のストックがなくなります。

それに過去に訪問した場所を再訪しても、新たに書くべきことがないことも多くなりました。

ムリに更新する必要もないと思いますので、本年からは段階的に10:00の更新をなくすつもりです。

10:00の更新は新たな本編を掲載する時だけにし、22:00の更新は今まで通り毎日継続する予定です。

今後も重箱の隅をつつくような内容になるかとは思いますが（笑）、よろしくお願い致します。


さて、今年は春からビッグウェーブが来ます。

近々、お知らせ致しますね！

「京都のおすすめ」の総合索引へ

謹賀新年

ーーーーーーーーーーーーーーーーーー

ちなみに今年は元日から早速、「お正月ご開帳めぐり」に出かけております。

「京都のおすすめ」の総合索引へ