2017 6/17の拝観報告（堀井七茗園に学ぶ 宇治茶の今昔 後編）

写真は、棠庵内部

製茶場を出て、縣神社方面に少し戻った途中に抹茶工場がありました。
今度はこの中へ。
内部の撮影は出来ましたが、なにか設備に特長があるのでしょう写真のweb掲載は禁止。
内部は簡単に言うと、たくさんの機械の臼が碾茶を抹茶に挽いています。
機械なので自動でグリグリ挽いています（笑）。
窓を開けて頂くと、抹茶のいい香りが充満しました。
また茶葉の質によって抹茶の粉の色も違うんですね。
比較的質が落ちるものは真緑色じゃなくて、やや黄色っぽいのですが、品質のいいのはきれいな緑色。
苔のような色でした。
15:00頃には抹茶工場を出て、縣神社へ向かいました。

こちらの堀井七茗園さんでは、個人での工場見学も可能です。
今回ご紹介した奧ノ山茶園、抹茶工場の見学と茶室 松風庵での成里乃の賞味で1人3000円だそうです。

さて今回我々も呈茶がありましたが、場所は縣神社の書院でした。
作年の献茶式で1度お邪魔しています。
こちらでまずは成里乃を1服頂きました。
非常にまろやかで苦みや渋みが全然ありませんでした。
成里乃をしっかり味わうため、お菓子は後から頂きました（笑）。

呈茶の後には書院の奥にある小間の棠庵も順に見学させて頂きました。

ずっと案内をして下さった堀井七茗園の社長さんのお話も知らなことばかりだったり、また楽しくお話しして下さったので非常に楽しいいい企画でした。

「京都のおすすめ」の総合索引へ

長男くんの塾の問題4（算数 図形1）

小学校5年生の長男ですが、最近は国語、理科、社会は塾の模試でも一定の結果をコンスタントに出しているので、もう本人に任せています。
しかし算数は苦手なようで、まだまでですね（笑）。
今回もハイクラスの講座の問題が分からず、質問してきました。
解答にやり方が書いておらず、答えの数しか書いてないのです。
まあやり方は「自分で考えろ」ということなのでしょう。

今回は2問あり、まず1問目が上です。
結構スタンダードな問題ですが、ハードルが2段階あります。

興味のある方は、考えてみて下さい。


解答
普通台形の面積といえば、（上底＋下底｝×高さ÷2ですが、今回はいずれの長さも分からないですね。
このように面積が公式で直接でない場合、解法は2つ。
1：より大きな図形から一部を引くことで、残りの面積として出す。
2：等積の別の形に置き換えて求める
のが定石でしょう。

今回は全体の形をみれば、1はキビシそうです。
なので2で攻めてみます。

問題に戻ります。
まず問題になるのは、中点Eの処理でしょう。
Eは弧BCの中点ですので、FはCDの中点などではない。
Eの使い方は、図2のようにAEを結んだ補助線を使うしかないのは、図形問題の経験を積めばわかります。
すると馴染みのある30°、60°の直角三角形が見えてきます。



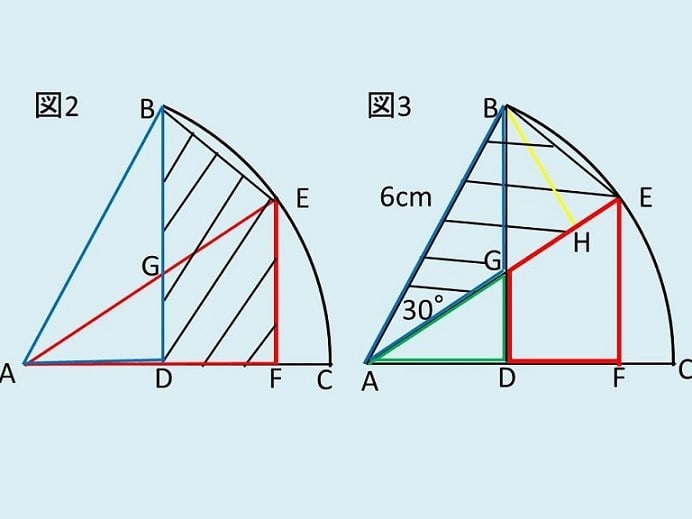
つまり図2の三角形AEFと三角形ABDは、斜辺が6cmの30°、60°の直角三角形なので合同であると分かります。
すると図3のように両者から三角形ADGを引いた、三角形ABGと台形DFEGの面積が同じです。

以上より
求めるべき台形BDFE＝三角形BGE＋台形DFEG
求めるべき台形BDFE＝三角形BGE＋三角形ABG
求めるべき台形BDFE＝三角形ABE
となります。

ここまでが1段階。

三角形ABEは6cmの2辺の内角が30°の三角形。
BからAEに垂線を降ろせば、三角形ABHは30°、60°の直角三角形なので、BHは3cm。
よって、
台形BDFE＝三角形ABE＝6(AE)×3(BH)÷2＝9㎠
となります。

・中点Eを正しく使えるか、
・60°があれば、30°90°の直角三角形を見出せるか、
が、解答のポイントですね。

「京都のおすすめ」の総合索引へ