昨年4月以来の望月教授の宇宙際タイヒミュラー理論ですが、「前回」とは異なり、今回は小難しい話はやめにして、誰もが知ってる”掛け算や足し算から宇宙理論を眺めて”みたいと思います。
IUT(宇宙際タイヒミュラー)理論とは、望月博士が約20年かけて築いた数学の理論で、”足し算やかけ算をする世界(=宇宙)を縦横無尽につなげ(=際)、数を自在に行き来させる(復元=タイヒミュラー)”という斬新なアイデアでした。
数学的に云えば、ABC予想の考察により、遠アーベル幾何などを拡大した圏の宇宙際(IU)幾何を構想した数論幾何学の理論である。
望月氏によれば、”楕円曲線を備えた数体のタイヒミュラー理論の算術版”となる。
もっと深く言えば、望月氏が2000年代に開発したp進タイヒミュラー理論や楕円曲線のホッジ=アラケロフ理論、及び数論的logScheme圏論的表示の構成等に続いた研究であり、一点抜き楕円曲線付き数体の”数論的タイヒミュラー変形を遠アーベル幾何等を用いて計算するIU幾何となる(ウィキより)。
IUT理論は、ABC予想およびそれに関連する予想をより深く理解するを目的として明示的に開発されました。
大まかに言えば、乗法的情報から加法構造を遠アーベル的な”復元”を行ない、算術変形は与えられた環の乗算を変更し、そのタスク(作業)は加算が変更された量を測定する事である。
遠アーベル的な復元や変形手順には、IUTの2つの主要な対称性(乗法演算と加法幾何学)を使用する。これは、望月氏のホッジ=アラケロフ理論に登場する特定の構造を一般化し、その間のリンクは従来の数論幾何学の外部で実行されます。
わかり易く云えば、掛け算は数論の世界に置いたままで、足し算は幾何の世界に送り分離させ、それぞれの世界で計算し、最後に足し算を数論の世界に戻す。その時の誤差を明確にし、証明が正しい事を確認する。
理屈は抜きにしてと言いたい所ですが、やはり数学はややこしい学問ですね。
以下、「ABC予想証明をめぐる数奇な物語」(後半)から大まかに簡単に纏めます。
全く新しい数学?
2012年8月30日、ネット上にABC予想を証明したとする論文が掲載された。
タイトルは「宇宙際タイヒミューラー理論」。著者は望月新一博士で、数学界は驚きと興奮に包まれます。
ところがその内容は、数学全体を”宇宙”と呼ぶだけでなく、”劇場”や”エイリアン”などと聞いた事もない単語が並ぶ数学理論だった。
エレンバーグは”まるで別の惑星から来た論文のようだ”と言った。とても奇妙で、本当に難しかった。
望月博士の理論では、数学の世界をもう1つ用意し、2つの数学世界を宇宙Aと宇宙Bと名付ける。わかり易く言えば、AとBの2つの宇宙を結ぶ写像をイメージする。
この2つの宇宙に、ある仕掛けを施す。
例えば、宇宙Aの数字1が宇宙Bでは1に、2は4に、3は9にと。つまり、Aの数はそれを2乗したBの数と繋がる。ここで、かけ算をやったとする。例えば、7×8はどうなるか。
Aの中では(普通の数の世界だから)7×8=56になり、Aと繋ったB宇宙では(もう1つの計算方法があり)、Aの7はBの49に、8は64に繋がるから、Aの7×8はBの49×64と一致する。つまり、答えは49×64=3136。
ではBの3136は、Aの数字を2乗したものがBの数字に繋がるから、Aの世界では√(3136)=56。故に、最初の7×8=56となり、辻褄が合う。
つまり、かけ算では繋がった2つの宇宙の中では成立する。数式で示せば、AB→A²B²かつ√(AB)←ABですね。
一方で写像で言えば、f:A→Bとするとf(x)=x²となり、x∈A,y∈Bの時はf(xy)=x²y²となります。故に、fの逆写像f⁻¹は√(x²y²)=xyとなり、上が成立します。つまり、掛け算の世界(写像)では2つの宇宙を行き来出来る。
因みに、ABC予想という数論の世界に、写像(復元)や群論(環)などの情景が現れるのもこの為です。
では”たし算”と言うと、宇宙Aでは7+8=15(当り前)ですが、宇宙Bでは7²+8²=49+64=113になる。が、これをAに戻すと√(113)となり、最初の15とは違う数になる。つまり、2つの宇宙を繋げると、たし算(を含むと)辻褄が合わなくなる。
言い換えれば、足し算の世界では2つの宇宙を行き来できなくなる。
望月博士が2つの宇宙を繋げた理由は、”かけ算は成立するが、たし算が成立しない数学世界を作りたい”という事でした。
”一個の数学ではできなかった、たし算とかけ算を独立に扱う柔軟性が必要ではないか!そういう発想だった”(加藤博士)
ABC予想証明の為の望月博士の戦略とは、かけ算だけが成立する世界を作り、たし算と切り離し、その世界を出発点に(たし算とかけ算にまつわる難問である)ABC予想の証明に辿り着くという、これまでにない奇抜なアプローチである。
因みに、1990年代以降、数々の数学者が証明へと挑み始めた「ABC予想」ですが、その一人にルシアン・シュピロ博士がいた。彼の戦略は、”ABC予想のAやBといった数を曲線に置き換え、それら曲線が交われば、ABC予想が正しいと証明できる”というものでした。
そしてついに、”2つの曲線が必ず交わる事を証明した”と確信。しかし博士は”直感的には2つの曲線は確かに交わる筈だったが、根本的な間違いがあった”事を認めた。
ABC予想の証明に生涯を捧げたシュピロ博士は、これ以降、数学の表舞台に姿を現さなくなった。その後、ABC予想は数学者たちの挑戦を尽くはねつける事になる。
一方で、望月教授がこの難問に取り組んだのが2000年の頃であるが、考えに考えた挙げ句、”無理である”事に気付いた。
故に”新しい数学を作る必要がある”と感じた。その”新しい数学”こそがIUT理論なのだ。
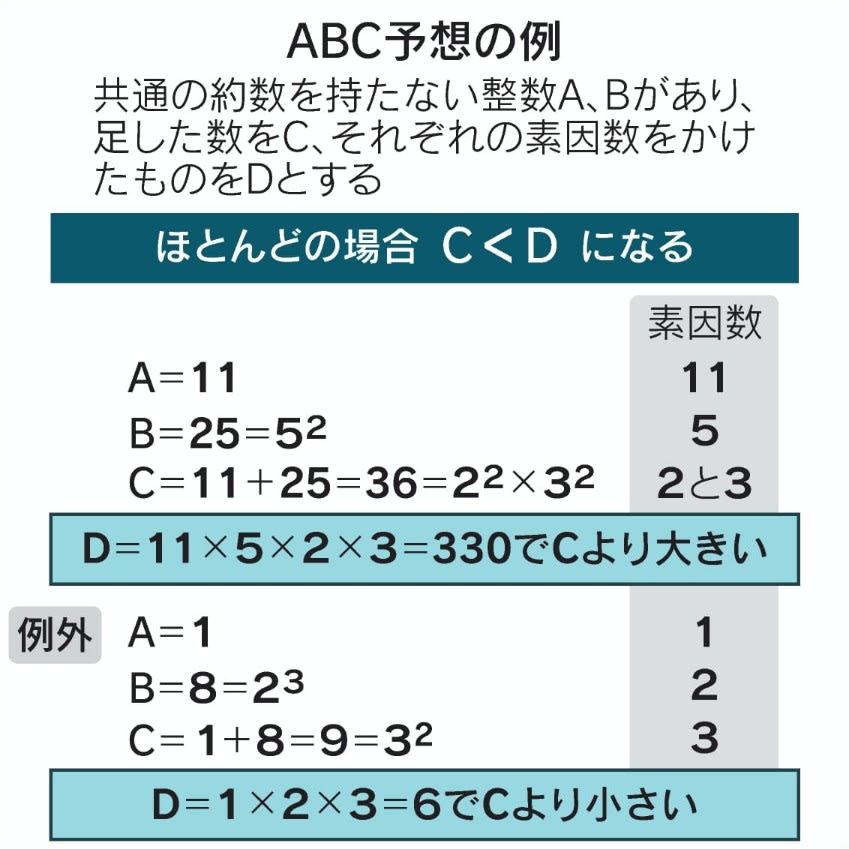
ABC予想は左側にはたし算、右側にかけ算が現れるが、(2つの宇宙を行き来できない)”たし算とかけ算を分離する”という根源的な課題に切り込んで行く。
更に望月氏は”異なるものを同じと見なす”現代数学の原理原則をも見直そうと考え始めまた。つまり、”同じものを異なるもの”とみなす。一度同じと見なしたものをもう一度異なるものだと考える。
いわば、”行ったり来たりできる数学”があってもいいのではないか・・・
本当はどうなの?
数学の世界で最も重要だともいわれる「ABC予想」は本当に証明されたのか?
2015年、国際会議が開かれ、望月博士を正しいと考える数学者たちと、疑問で頭が一杯の数学者たちとで激論が交わされた。
問題となったのは、宇宙際タイヒミューラー理論が出発点とした、2つの数学世界。全く同じもので(実は違うもの)だと説明される2つの数学世界。
デイビッド・ロバーツ博士は、”望月の理論で奇妙なのは、まずは全く同じものとしながら、次に完全に異なるものとして扱う点。数学では同じと見なせるものは同じとするのが原理原則だが、同じでありながら同時に異なるものなんてありえるのか?・・・絶対無理ですよ”と反論する。
更にデュピー 博士は、”誰かがある物を持ってて、<それはこれと同じものでもあるし、同時に異なる物である>と言った時の様な違和感。多くの数学者は、それは<2が4と等しい>と言ってるのと同じで、数学は破綻する”と語った。
結局、議論は紛糾し、証明の核心へと迫る前に会議は閉会となる。
2018年には、同年にフィールズ賞を受賞したボン大学のペーター・ショルツ博士(30)が来日し、望月博士と激論を交わした。
しかし前者は数学の原則を主張し、後者は”原則を当てはめるべきでない”と主張。結局は平行線のままに終わる。
これまで数学とは、1つ1つ論理を積み上げ、同じ結論に達する学問とのイメージが強かった。が今回は想定外な事が起きている。
この混乱と分裂は何を意味するのか?
望月博士が証明を作り上げる過程をみつめてきた加藤文元博士は、”数学者同士が理解し合えない今の状況は、現代数学が新しい数学へと飛躍する為の準備段階かもしれない”と語る。
”数学的な意味で、(証明に)何かギャップがあるとか、正しさに少し曇りがあるとかではない。今回の場合、やはり対象に関する認識の違いです”とも語る。
対象に関する認識論の違いが互いの理解を阻むとは、どういう事なのか?
数学は異なるものを同じと見なすという方法で始まり発展してきた。つまり、物事の異なる部分に目を瞑り、同じと見なせる部分に注目し認識する事を(数学は)原理原則としてきた。
加藤博士は”我々は<同じものでも違うものと見なす>という事をやってる訳ですが。ある時は<同じものを違う>と見なすし、ある時は<同じものを同じ>と見なす”と語る。
つまり人間の思考は、2つを同じと認識する事もあれば、同時に全く違うものだと考える事もある。いわば矛盾をも包み込む高い柔軟性を持つ。だから数学も、そうした柔軟な形へと進化(変異)する道があってもいいのではないか。
”IUT(宇宙際タイヒミューラー理論)というのは、数学の基本的な深層の所を揺るがす地殻変動から起こる理論だから、現今の数学との違いを完全に言語化する、新しい数学の言語体系を早急に作るべきである”(加藤博士)
かつての指導教官のファルティングス博士もまた、これまでの数学との違いを”分かりやすく説明する言葉を見つけてほしい”と語る。
”望月は説明に力を入れるべきです。今はなぜ彼のアイデアが上手くいくのか分かり難いのです”(ファルディングス)
このままでは望月氏の証明は忘れ去られるのだろうか?”
”その恐れはあります。誰かが望月の理論を分かる様に説明する言葉を見つけてくれれば・・・”
若者たちが動き出した
論文発表からまもなく10年。望月理論に”未来の数学の姿を見い出す”という若い数学者たちがネット上での議論を開始した。
”望月の件に巻き込まれるなと警告する数学者もいる。<キャリアがむちゃくちゃになるぞ>と。でもこれは微分積分の発明や重力の発見にも匹敵する革命で、私は今それに立ち会っている。100年後いや200年後も、望月理論は数学の世界で生き続けてると思う”とデュピー博士は未来を語る。
一方で、望月氏も動き始めた。
多くの数学者が理解できない”同じものでもあり異なるものでもある”という(一見矛盾に思える)論理展開を詳しく解説する文章を公表。更に、自らの言葉で以下のメッセージを数学界に発信した。
”数学者の中には、IUT理論がこれまでの数学とは関係ない別物だという人がいます。が私は、この理論もまた多くの数学者が研究する数学と繋がっている・・・数学者同士もまた繋がってると信じています”
最後に、NHKでは以下の様に締め括る。
ABC予想を証明したという望月理論が、今後世界の数学者に広く受け入れられるか?それはまだ分からない。
しかしもし、これが新しい数学の夜明けであれば、私たちは史上まれにみる”知の大変革”を目撃してる事になる。それだけは言える。
望月博士と京大数理研の星裕一郎准教授、ノッティンガム大のイワン・フェセンコ教授ら5人はIUT理論を拡張し、”足し算とかけ算に関係する特別な不等式”を導き、最終定理の式に代入し、フェルマーの最終定理の(完全なる)別証明に行き着いたという。
従来のIUT理論では、この不等式に未知の変数があったが、今回この値を特定出来た事が突破口に繋がった。但し、この論文は東京工業大が発行する数学誌「KodaiMath.J.」に掲載される(朝日デジタル)。
一方で、この5人は2020年11月にも、IUT理論を(非明示的な定数が現れない)事に精密化させ、強いABC予想の証明やフェルマーの最終定理の別証明への適用を拡げていた。
計算する数論幾何学の理論とされるIUT(宇宙際タイヒミュラー)の最初の進展は、原論文の帰結による”弱い”ABC予想や楕円曲線ではスピロ予想、楕円曲線のフライ予想などへの適用である。
2つ目の進展は(先述の)フェルマーの別証明であり、3つ目の進展としては、IUTにおけるテータ関数を(メリン変換により)リーマンゼータ関数と関係を期待した研究である。
つまり、IUT理論と(リーマンゼータを一般化した)ディリクレのL関数の零点の間に数学的な関係があるとされ、L関数の零点で応用が検討されている。
その他の進展としては、高機能暗号への暗号理論的な検討などで、これも応用が検討されている(ウィキ)。
以上、IUT理論が秘める未来は、哲学的で非論理的な部分も含まなくもないですが、正しい事が証明されれば、とても壮大な宇宙理論とも言えますね。
追記
今年の7月、ABC予想を証明したとする望月教授の理論について、ドワンゴ創業者の川上量生氏は”本質的な欠陥”を示した数学者に100万ドル(約1億4千万円)贈ると発表した。
望月理論(IUT理論)は未解決の難問であるABC予想の証明を含み、論文は7年以上かけて審査されたが、”証明に問題がある”との声もあり、IUT理論をめぐる議論は停滞したままだ。
IUT理論の研究所所長の加藤氏は”IUT理論は残念ながら欧米の数学者に高く評価されているとは言い難い。最初の論文発表から10年以上経っても京大以外に研究のコミュニティーができておらず、数学史の中でも異常な状況だ。しかし(賞の創設により)若い世代を含めモチベーションのある研究者が参入できる環境にする”と語る。
ABC予想は整数の足し算(左辺)とかけ算(右辺)の関係にまつわるもので”整数論の基本にメスを入れるべき問題であり、解決できた時の波及効果は非常に大きい”(日本経済新聞)とされる。










5億円も稼ぐんだから
数学の未解決難問とされるabc予想にたかが100万ドルじゃ、数学者は浮かばれない。
この10倍じゃないと寄り付かんろうね。
ガウスが語ったように
整数論というのは証明も反証も幾らでも書き出せるから、みんな避けるんだよ。
自殺行為とはそういうことなんだろう。
フェルマーの定理だって
最初は200万ドルほどだったとされるが、一時は誰も寄り付かなくなって5万ドル程にまで下がった。
しかし、ワイルズは代数幾何と複素解析を(谷山・志村の)モジュラリティ定理を証明する事で結びつけ、遠く離れた2つの世界を1つにした。
ワイルズの幸運は谷山や志村に加え、多くの天才数学者に恵まれた事が大きい。
彼らが数学界に与えた功績をお金に換算すれば懸賞金の1千倍は下らんだろうけど、数学は今も昔もカネにならないんだよな。
リベットやフライ、ワイルズの師匠のメイザーや弟子のテイラーなどもとても大きな貢献を果たしました。
大体において、難題を解く時は全く異なる2つの領域を結びつけるんですが、望月理論では”同じものを2つに分離し、再び同じものにする”という、少し不可解な部分もありますね。
ダイヒミュラーという変換理論は興味あるんですが、あまりに飛躍が大きすぎて・・・
ワイルズの場合は100ページの論文で済んだんですが、望月氏の場合は700頁。これを全て読んで理解する数学者がいるのか?どうかも疑問です。
何だか頭が混乱してきました。
小難しい記事に、コメント有難うございます。