わずか1組しかない三角形のペア〜現代の数論と古代ギリシャの幾何学はこうして結びつく

　｢宇宙から来た変換理論・・｣で､IUT(変換)理論での重要な復元ツールとなる”遠アーベル幾何学”の説明をしましたが､”遠アーベル幾何学”で検索すると､以下の記事に遭遇した。

　慶應大学の研究グループは2018年9月､”辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には､周の長さも面積も共に等しい組が(相似を除き)僅か1組しかない”という､これまで未解決とされた定理の証明に成功したと発表。この定理は一見初等的であるが､証明には20世紀末に開発された比較的新しい｢数論幾何学｣の手法が用いられた。
　高度に抽象化された現代数学にて､この様な身近な応用例が得られる事は非常に珍しいという。
　因みに､古代ギリシャ時代以来､何人もの数学者達が”辺の長さと面積が全て有理数である三角形”を探求してきた。この様な三角形を”有理三角形”と呼ぶが､こうした三角形の周の長さや面積を測量する事は幾何学の分野であり､有理三角形を周の長さや面積で分類する問題として考えられてきた。
　今までに､"周の長さ同士が等しく､かつ面積同士が等しい有理三角形の組は無限にある"事が判っている。そして今回､慶大のグループが新たに発見したのが”周の長さ同士が等しく､かつ面積同士も等しい有理直角三角形と有理二等辺三角形の組が(相似を除き)たった1組しかない”との定理である。
　以下､｢1組しかない三角形の組――｣に補足を加えて紹介します。

周の長さも面積も共に等しい三角形

　前述の様に､線の長さや図形の面積を測る問題は基本的な幾何学的対象である。
　例えば､辺の長さが3と4と5の直角三角形は皆がよく知る図形だが､”辺の長さが全て整数となる直角三角形はどれ位あるか？”という問題は古代ギリシャ時代から研究されてきた。更に､”辺の長さが全て整数となる直角三角形の組の中には､周の長さも面積も共に等しい組がどれ位あるのか？”という問題なども研究されていたと推測される。
　これら幾何学の問題は､全て”種数(=貫通穴の数)が0の代数曲線上の有理点(=点の座標が有理数)集合の決定”という代数学の問題に置き換える事ができる。

　そこで､代数方程式の解の集合として定まる図形を代数多様体と呼ぶが､特に(三角形の様な)1次元の図形は”代数曲線”と呼ばれ､その主な例として､xy平面内の直線y=xや､放物線y=x²､円周x²+y²=1などがある。
　一方､方程式の複素数解の集合から定まる代数曲線は､貫通穴を持つ多様体である浮き輪が幾つか連結した図形に例えられ､浮き輪の数が種数となる(図3)。故に､直線や円周や放物線の1次元図形(代数曲線)の種数は0と言える。また(厳密には)有理点とは､代数多様体上の点のうち､代数方程式の有理数解に対応する点と言える。

　因みに､この種数0の代数曲線上の有理点集合の決定問題は”有理一意化”と呼ぶ手法により解ける事が､少なくとも座標幾何学が誕生した17世紀には知られていた。但し､”有理一意化”とは代数曲線上の有理点を一意的に求める事で､個々の代数曲線上の有理点集合を完全に決定すると言える。が故に”有理点集合の決定問題”と呼ばれてきた。
　しかし､フェルマー方程式:xⁿ+yⁿ=1の様な”種数が1以上の代数曲線上の有理点集合の決定”に帰着される問題には､今でも統一的な解法は知られていない。　
　この難問の解決に動機付けられ､20世紀に現代数学の1分野である(冒頭でも紹介した)｢数論幾何学｣が大きく発展する事となる。

　慶大理工学研究科数論幾何グループの平川義之輔(博士課程3年)と松村英樹(同2年)は､”辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には､周の長さも面積も共に等しい組が(相似を除き)たった1組しかない”という定理を証明する為に､まず問題となる三角形の組を種数2の代数曲線でパラメーター付けし､”特殊な種数2の代数曲線上の有理点集合の決定”という別の問題に帰着させた。
　この様な代数曲線上には”有理点が有限個しかない”事は知られてたが､更に､個々の代数曲線上の有理点集合を完全に決定する為に､｢p進アーベル積分論｣に基づく｢Chabauty-Coleman法｣と呼ぶ解析的手法を用いるが､慶大のグループは”有理点が10個しかない”事を突き止めた。

代数曲線上の有理点集合の未解決問題　

　そこで､得られた10個の有理点のうち8個は”辺の長さが0または負となる潰れた三角形の組”に対応するが､残りの2個の有理点は”周の長さと面積が共に等しい三角形の組”に対応する事が分かった。
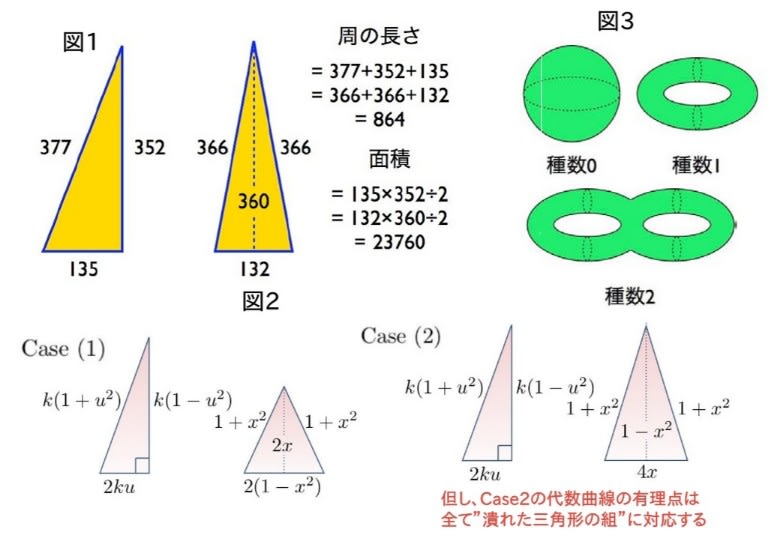
　例えば､直角三角形と二等辺三角形の組の辺の長さは､ある正の有理数x,u,k(共に>0)を用い､[図2]の様に2組のパターン(Case)で表される。
　まず､Case1の左の直角三角形では長い方からk(1+u²),k(1−u²),2kuとなり､同右の二等辺三角形では(垂線の長さが2xより)1+x²,2(1−x²)となる。同様に､Case2ではそれぞれ､k(1+u²),k(1−u²),2ku､及び(垂線の長さが1−x²より)1+x²,4xとなる。
　因みに､Case1では､y²=(x³−x+6)²−32という”種数2の代数曲線”の有理点(方程式の有理数解)を全て決定するのだが､上述したColeman法を使い､この代数曲線上には有理点が10個しかない事を証明した。その内の8個は”潰れた三角形”に､残り2つは[図1]の2つの三角形に対応する。

　但し､Coleman法を実行する際､代数曲線の”モーデル-ヴェイユ群”のランクが種数よりも小さくなる必要があるが､｢2-降下法｣と呼ぶ手法により､モーデル-ヴェイユ群のランクが1である事が証明でき､問題点を克服した。　
　更にCase2も､Case1で述べた”代数曲線の有理点集合の決定”に帰着するが､この代数曲線の有理点の10個は全て”潰れた三角形の組”に対応する(上図2-右)。

　実際に､Case1を計算すると､直角三角形と二等辺三角形の周の長さが等しい事よりk+ku=2を､また面積が等しい事よりk²u(1−u²)=2x(1−x²)を得て､この連立方程式を解く事で､変数x,kの方程式:2k²−(x³−x+6)k+4=0を得る。但し､0<k<2tなる事に留意する。
　以下､｢A unique pair of triangles｣を参考に大まかに纏めます。
　ここで変数kを変数yに置き換え､次数を上げて平方をとり､”種数2の代数曲線”を作る。ここら辺が少しややこしいが､この代数曲線はy²=(x³−x+6)²−32と変数x,yの方程式になり､これを解けば､(x,y)=(0,±2)､(1,±2)､(−1,±2)と2つの(5/6,±217/216)と､合計10個の有理点(有理数解)を得る。
　先述した様に､この10個の有理点のうち8個は”潰れた三角形”に対応し､残りの2つの有理点(x,y)=(5/6,±217/216)は､(k,u,x)=(27/16,5/27,5/6)と(32/27,11/16,5/6)に相当し､[図1]の三角形の組の様に､3辺の長さの整数比が377:352:135の直角三角形と､3辺の長さの整数比が366:366:132の二等辺三角形に相当する。
　そこで､各々の周の長さが(比を長さとすれば)864(=377+352+135=366+366+132)で､各々の面積が23760(135×352÷2=132×360÷2)となり､同じ値になる。

　Case2も同様に､k+ku=1+x²+2xとk²u(1−u²)=2x(1−x²)の連立方程式を得て､w=u+1として整理すると､2wk²+(−3w³+2w²−6w+4)k⁵+w=0を得る(但し､w>1,k>0)。ここで上と同様に､変数kを変数rに換え､次数を上げて平方をとり､種数2の代数曲線:r²=(−3w³+2w²−6w+4)−8w⁶を作る。この変数w,rの方程式を解くと､(w,r)=(0,±4)､(1,±1)､(2,±8)と2つの(12,±868)と､合計10個の有理点(有理数解)を得る。だが､この10個の有理点は全て”潰れた三角形”に対応する。
　以上､”Journal of Number Theory(原文)”からでした。

　以上､”辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には､周の長さも面積も共に等しい組が(相似を除き)たった1組しかない”という新たな定理の証明をめでたく得る事が出来た。
　だが例えば､3辺の長さが20,16,12の直角三角形と､同じく3辺の長さが15,15,18の二等辺三角形では周の長さはどちらも48(20+16+12=15+15+12)で同じだが､面積は96(12×16÷2)≠108(18×12÷2)と異なるが､(前述した様に)こうした組み合わせは無数に存在する事も判っている。

　今回解決した問題は､古代ギリシャ時代にも考察されてたと考えられてはいるが､証明に使われた｢Coleman法｣と｢2-降下法｣は共に1980年代以降に開発された比較的新しい手法である。そして､この様な古代ギリシャ時代の素朴な問題と､現代の洗練された解決手法の対比､そして時代の大きな隔りを伴う研究成果は､数学の美しさを引き立てる貴重な成果であると言える。
　高度に抽象化された現代数学にて､この様な身近な応用例が得られる事は非常に珍しいという。

補足〜専門用語の説明

　専門用語の解説だが､前述の｢A unique pair of triangles｣(和訳版)その他を参考に､私が理解できる範囲で解説します。
　まずは､代数体K上で定義された楕円曲線の有理点の群をモーデル-ヴェイユ群E(K)とすると､｢モーデルｰヴェイユの定理｣によりE(K)が有限生成である事が示されるが､その生成元の個数､つまりランクを決定するのが困難とされる。
　そこで､”セルマー群”を使ってランクを計算する為に｢2-降下法｣を用いるのだが､簡単に言えば､目的の三角形の組全体の集合を種数が2以上の代数曲線(例えば超楕円曲線)の有理点に対応させる事ができる。
　また､こうした有理点を持つ代数曲線は､ヤコビ多様体と呼ばれる高次元の代数多様体に標準的な方法で埋め込む事が出来る。従って､ヤコビ多様体の有理点集合は有限生成アーベル群をなすが､これがモーデル-ヴェイユ群となり､この群のランク(階数)を”Mordell-Weil rank”と呼ぶ。
　つまり､ヤコビ多様体というアーベル多様体を作る事が出来､そのアーベル多様体のモーデル-ヴェイユ群に対し､同じランク(階級)を考える事ができる。例えば､この群のランクが正である事と無限群である事は同値と言える。

　そこで､三角形のペアの一意性を示す為に｢Chabauty-Coleman 法｣を使う訳だが､上述した様に､群のランクが1以下である事を示す為に､｢2-降下法｣が用いられたる。
　つまり､楕円曲線Eのモーデルｰヴェイユ群E(Q)のランクを評価する為の有効なツールとなるのが方法が｢2-降下法｣となるが､簡単に言えば､E(Q)/mE(Q)という群の”大きさ”を測る方法だ。但し､E(Q)/mE(Q)は”mE(Q)のE(Q)による剰余群”と呼ばれ､群mE(Q)(⊃E(Q))の元がグループ分け(分割)出来る事を示す。

　ヤコビ多様体の”Mordell-Weil rank”の決定は通常は困難だが､応用上はその上界(上限値)を与える事で十分とされる事も多く､例えば､E(Q)/mE(Q)がすっぽり収まる様な(セルマー群なる)群を考え､セルマー群の位数を評価する事で､E(Q)/mE(Qの大きさを評価する。更に､このmにはm≥2を用いる事が出来､m=2がよく用いられる事から､”2-降下法”と呼ばれる。
　但し､セルマー群とはアーベル多様体の同種写像から作られる群の事で､完全系列の中央のセルマー群は有限で実効的に計算可能とされる(弱いモーデルの定理)。
　少し平ペッたく言えば､Mordell-Weil群をコホモロジー群や､古典的でディファントスな不変量の計算に帰着する”2-セルマー”群という計算が容易な”入れ物”に埋め込み､その”入れ物”の大きさを計算する事で､”Mordell-Weil rank”の上限値を与える手法とも言える。

最後に

　以上､理解し難い所も多々あるとは思いますが､古代ギリシャの数学者たちが眺めたであろう数学(特に幾何学)の景色を､昨今の若き日本の数学者たちが代数学(数論)に置き換えて解き明かした。
　この事実は､”三角形の周の長さと面積を測る”という身近な問題とは言え､抽象化という現代数学の大きな壁が立ちはだかるにも関わらず､洗練された証明を与えた事は､我ら日本人にしてもとても誇らしい事である。

　日本の議会民主政治が急速に腐っていく今､こうした日本の若き数学者の偉業は､これからの日本を支える大きな礎になる筈だ。
　改めて､古代ギリシャの古典数学と現代数学に乾杯！