複利法とは、元金によって生じた利子を次期(次年)の元金に組み込んでいく方式です。例えば「元金をS0,年利をr」の条件で預金すると、次のように預金額は増えて行きます。
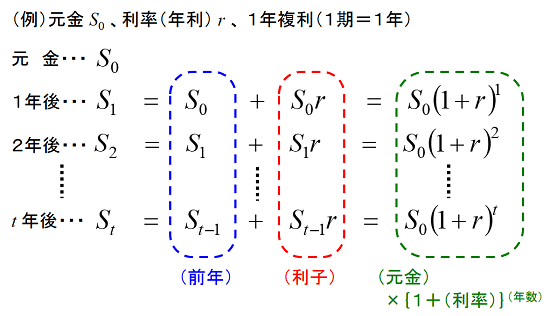
1年後には元金S0に利子S0r(=利率×元金)が新たに組み込まれる形で、元利合計(預金額)が増えていきます。
2年後には元金S1に利子S1r(=利率×元金)が新たに組み込まれる形で、元利合計(預金額)が増えていきます。
つまり、1年後の預金額をS1、2年後の預金額をS2…t年後の預金額をStとすると、この間預金の出し入れや、利率の見直しが発生しないものと仮定すると
(t年後の預金額)=(元金)×{1+(利率)}(年数)
のように表すことができます。
上の例では1年ごとに利子が上乗せされる条件(1年複利)を想定しました。これがもし、半年ごとに利子を上乗せする場合(半年複利)は、1年を2期に分けるので、半年ごとに利率(r/2)分ずつ、つまり、1年の間に2回、利子が上乗せされます。

同様にして、1年をn期に分ける場合(1/n年複利)は、1/n年ごとに利率(r/n)分ずつ、つまり、1年の間にn回、利子が上乗せされます。この回数nを∞に持っていくと、連続的に利子が上乗せされることになります。つまり、連続的に預金が増加するということです。
ネイピア数eを用いると、1年後の元利合計S1は簡単に記述することができます。
ここで、元金をS0,年利をrの連続複利で運用する場合を考えてみます。この場合、次のようになるので

このイメージをグラフで表してみます。

通常の1年複利や半年複利の場合は、1年毎または半年毎に元利合計が増えて行くので、資産価値は階段状に上っていきます。この感覚を細かくしていくと、やがて、滑らかなカーブに近づいていきます。このカーブが連続複利に相当します。実際問題としては一定の時間間隔ごとに、段階的に預金が増加する(利子が上乗せされる)わけですが、理論的に解析する際は、連続的な関数の方が数学的にも扱いやすいので、連続金利を用います。

















