オプションとは、将来の一定期間に、約束した金額で金融商品(金融資産)を売ったり、買ったりする事ができる「権利」です。ある金融資産を例にとって考えてみましょう。
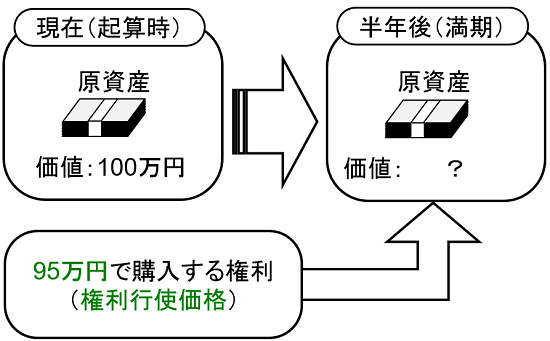
この金融資産は最初の時点(起算時)で100万円の資産価値を持っているものとします。
この金融資産を「半年後に購入しよう」とした場合、幾らで購入できるでしょうか?・・・それは半年後にならないと判りません。しかし、早めに購入することを決めておかないと、他の投資家に先に購入されてしまうかもしれません。
そこで、半年後に「95万円」で購入する「権利」を、今の内に購入してしまうのです。この権利がオプションです。
この時、売買対象の金融資産のことを「原資産」、半年後と言う時期のことを「満期」、95万円という価格を「権利行使価格」または「ストライク」と言います。
オプション取引の対象となる金融資産は、その資産価値(資産価格)が時々刻々と上下に激しく変動するします。このような資産を運用した場合、大きな利益を上げることも期待できる半面、元本割れを起こしてしまう危険性もはらんでいます。このような金融資産を「危険資産」と言います。

危険資産を数理モデルで表現する際は、平均的な変動(トレンド)は安全資産に準じるものとして、さらに不規則に変動する成分(ノイズ)を考慮します。ここで、トレンドの利率をリターン(μ)、ノイズの変動の大きさをリスク、またはボラティリティ(σ)と言います。
危険資産の利率は確率的に変動します。有名なブラック・ショールズモデルでは、その確率分布を「正規分布」と仮定しているのが特徴です。
続いて、満期時の資産価格とオプションの取り扱いについて考えてみましょう。

満期(半年後)の時点で、この原資産(金融資産)の価格が暴落して、95万円を下回った場合、このオプションを「放棄」することで、損失を免れることができます。
一方、満期(半年後)の時点で、原資産(金融資産)の価格が高騰して、95万円を上回った場合は、このオプションを「行使」することで、差額分だけ利得が発生します。

オプション取引を行う際は、予め「使用料」を支払う必要があります。このオプションの価格(価値)のことを「プレミアム」と言います。
オプション取引に伴う利得は青のグラフで表されますが、実際には既にプレミアムを支払っている状態なので、実際の収支は青のグラフよりもプレミアム分だけ下にシフトした赤のグラフのようになります。
プレミアムは、将来時点で見込める利得を、現在時点での価値に換算したものです。オプション取引では、原資産の価値が時間と共に変動しています。これに伴って、オプションの価値・プレミアムもまた、時間的に変動しています。
このような原資産の価格やプレミアムの時間的な変動を数値シミュレーションで見てみましょう。
【 設定条件 】
資産価格の初期値:S0 = 100[万円]
リターン :μ = 3[%/年]
ボラティリティ :σ = 10[%]
無リスク利子率 :r = 3[%/年]
時間間隔 :Δt = 1[日]
積分期間 :T = 183[日]
まずは原資産の価格変動です。

今回は起算時点から満期までの価格変動のシナリオを2000パターン計算しています。183日間に渡る価格変動をグラフに重ねてみました。時間が経つにつれて、変動の幅が広がる様子が判ります。
なお、確率微分方程式の数値解法はエクスプリシット法(時間積分)とモンテカルロ法(ランダム変動)を使用しています。また、乱数生成においてはフォン・ノイマンの棄却法を適用しています。
続いて、満期時点での資産価値の予測を見てみましょう。2000パターンのシナリオを基に、満期時点での資産価値の分布をヒストグラムで表示してみます。

満期時点における資産価格は確率的に決まりますが、その分布は正規分布に従う様子が判ります。そもそも資産価値の確率微分方程式が正規分布に従っているので、その性質が反映されたものと考えられます。
そして、いよいよ「プレミアム」の時間的な変動です。

プレミアムは各時点における資産価値S(t)と権利行使価格K、さらに無リスク利子率rを用いて計算します。
プレミアムは「期待値」で表されるため、予め2000パターンの各々における決済額(利得)を計算し、その平均を求めます。この平均値に対し、無リスク利子率と時点(日数)から決まるディスカウント・ファクターを乗じることで、プレミアムとしています。
プレミアムは時間の経過と共に増加していく傾向が表れています。細かい上下変動を伴っていますが、概ね安定的に右肩上がりとなっているようです。プレミアムの価値は原資産の価値から派生しているため、その変動の性質も危険資産に準じています。その様子も視覚的に理解することが出来ます。

















