1か月ほど前の記事「前線形成と鉛直循環の励起」では、水平面上において地衡風による温度場(温位場)の変化が生じると、二次的な鉛直循環が励起されることを紹介しました。
そして、この鉛直循環は、地衡風による温度場(温位場)の変化によって生じた温度風バランスの崩れを解消する(基に戻す)働きを持っていました。

水平面で地衡風の収束が生じ、フロントジェネシス(前線強化・温位傾度が増大)を生じると、鉛直面ではフロントリシス(前線消滅・温位傾度が減少)の二次循環を生じます。
一方、水平面で地衡風の発散が生じ、フロントリシスを生じると、鉛直面ではフロントジェネシスの二次循環を生じます。
このような「水平面上の温度場(温位場)の変化」と「鉛直循環の発生」を関連付ける指標として「Qベクトル」が用いられます。Qベクトルの定義は、主に次の式が用いられます。

この式を、水平面上におけるフロントジェネシスとフロントリシスの各ケースについて適用してみます。まずは、各ケースについて、ごく簡単な条件を設定してみましょう。

水平面(x-y平面)上に等温線を3本引いています。つまり、y方向に温度傾度を生じています。ここで、同じくy方向の地衡風を仮定します。
いま、対象領域(水色の正方形)の中心「●」におけるQベクトルを考えます。簡単のため、正方形のx方向、y方向の距離(Δx、Δy)は単位長さ(=1)とします。
フロントジェネシス(左側)では、y方向の地衡風(上・-v,下・+v)が対象領域の中心に向かうように収束しています。このため、温度傾度が増大する(等温線の間隔が狭まる)ように推移します。
フロントリシス(右側)では、y方向の地衡風(上・+v,下・-v)が対象領域の中心から離れるように発散しています。このため、温度傾度が減少する(等温線の間隔が広がる)ように推移します。
各ケースで仮定した条件をQベクトルの定義式に適用します。

このように、各ケースにおけるQベクトルが得られました。式だけを見ても判りにくいので、先ほどの図にQベクトルを重ねて書いてみます。Qベクトルは赤で示しました。
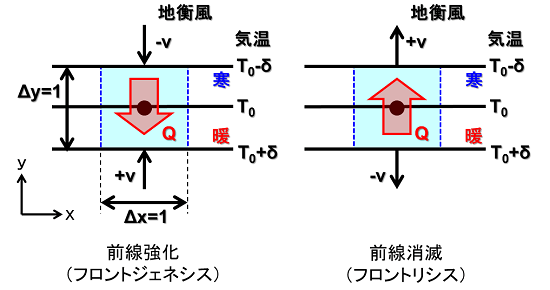
フロントジェネシスの場合(左側)、Qベクトルはy軸負の向きとなりました。等温線に垂直で、暖気側を指しています。
フロントリシスの場合(右側)、Qベクトルはy軸正の向きとなりました。等温線に垂直で、寒気側を指しています。
それで、Qベクトルと鉛直循環の間にはどのような関係があるのでしょうか。冒頭の図に倣って、立体的に考えてみましょう。

冒頭の図をベースにQベクトルを重ねてみました。この結果、Qベクトルの指す側で上昇流、反対側で下降流となるような鉛直循環が励起されることが判ります。
ここまでは、水平面上における等温線と地衡風が垂直に交わる場合を考えてきました。続いては、等温線と地衡風が互いに斜めの場合を考えてみましょう。

今回は一例として、斜めの地衡風に伴って温度場自体が(等温線の間隔を保ちながら)回転するような場合を想定してみます。
上の図で仮定した条件をQベクトルの定義式に適用します。

得られたQベクトルを、図に重ねて書いてみます。これまでと同様にQベクトルは赤で示しました。
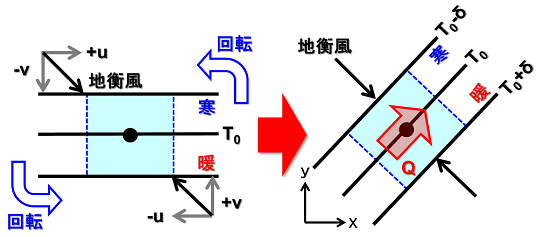
Qベクトルはx軸、y軸共に正の向きとなりました。等温線に平行な向きを指しています。
さて、一般的なQベクトルと鉛直流の関係については、Qベクトルを用いたオメガ方程式で説明されます。この辺の話はまたの機会に。
そして、この鉛直循環は、地衡風による温度場(温位場)の変化によって生じた温度風バランスの崩れを解消する(基に戻す)働きを持っていました。

水平面で地衡風の収束が生じ、フロントジェネシス(前線強化・温位傾度が増大)を生じると、鉛直面ではフロントリシス(前線消滅・温位傾度が減少)の二次循環を生じます。
一方、水平面で地衡風の発散が生じ、フロントリシスを生じると、鉛直面ではフロントジェネシスの二次循環を生じます。
このような「水平面上の温度場(温位場)の変化」と「鉛直循環の発生」を関連付ける指標として「Qベクトル」が用いられます。Qベクトルの定義は、主に次の式が用いられます。

この式を、水平面上におけるフロントジェネシスとフロントリシスの各ケースについて適用してみます。まずは、各ケースについて、ごく簡単な条件を設定してみましょう。

水平面(x-y平面)上に等温線を3本引いています。つまり、y方向に温度傾度を生じています。ここで、同じくy方向の地衡風を仮定します。
いま、対象領域(水色の正方形)の中心「●」におけるQベクトルを考えます。簡単のため、正方形のx方向、y方向の距離(Δx、Δy)は単位長さ(=1)とします。
フロントジェネシス(左側)では、y方向の地衡風(上・-v,下・+v)が対象領域の中心に向かうように収束しています。このため、温度傾度が増大する(等温線の間隔が狭まる)ように推移します。
フロントリシス(右側)では、y方向の地衡風(上・+v,下・-v)が対象領域の中心から離れるように発散しています。このため、温度傾度が減少する(等温線の間隔が広がる)ように推移します。
各ケースで仮定した条件をQベクトルの定義式に適用します。

このように、各ケースにおけるQベクトルが得られました。式だけを見ても判りにくいので、先ほどの図にQベクトルを重ねて書いてみます。Qベクトルは赤で示しました。

フロントジェネシスの場合(左側)、Qベクトルはy軸負の向きとなりました。等温線に垂直で、暖気側を指しています。
フロントリシスの場合(右側)、Qベクトルはy軸正の向きとなりました。等温線に垂直で、寒気側を指しています。
それで、Qベクトルと鉛直循環の間にはどのような関係があるのでしょうか。冒頭の図に倣って、立体的に考えてみましょう。

冒頭の図をベースにQベクトルを重ねてみました。この結果、Qベクトルの指す側で上昇流、反対側で下降流となるような鉛直循環が励起されることが判ります。
ここまでは、水平面上における等温線と地衡風が垂直に交わる場合を考えてきました。続いては、等温線と地衡風が互いに斜めの場合を考えてみましょう。

今回は一例として、斜めの地衡風に伴って温度場自体が(等温線の間隔を保ちながら)回転するような場合を想定してみます。
上の図で仮定した条件をQベクトルの定義式に適用します。

得られたQベクトルを、図に重ねて書いてみます。これまでと同様にQベクトルは赤で示しました。

Qベクトルはx軸、y軸共に正の向きとなりました。等温線に平行な向きを指しています。
さて、一般的なQベクトルと鉛直流の関係については、Qベクトルを用いたオメガ方程式で説明されます。この辺の話はまたの機会に。

















