2023.08.19(土曜日) 晴れ
ウィーンブリッジ発振器のことが少し分かった。(と、本人は申しておりますが・・・)
発振を起こすには正帰還される信号の強さが必要・・・
波形をきれいにするには負帰還量が多い方が良い・・・
だけど、負帰還量が多すぎると発振は停止してしまうので、この兼ね合いが難しい。
ところで、どうして発振周波数が決まるんだろう?
C と R で構成されたバンドパスフィルターがその働きをしているんだそうだが
参考書には何やら難しい計算式が書いてあってチンプンカンプンだ。
周波数可変の正弦波発振器ができたので、その出力をバンドパスに入力して出力を観察
してみよう。

先ず CT = 0.01μF、 RT = 50KΩ にして観察してみた。
この場合は参考書の計算式によると f= 1/2π RT CT (Hz) で
結果は318Hzとなったが果たして・・・
オシロスコープのCH1にB.P.Fの入力を接続、CH2に出力を接続しして観察。
318Hzよりだいぶ低い160Hz付近を入力した。
その結果のの画面。 出力の位相が進んでいる。

周波数を上げて行く。
出力の位相がだんだん遅れてくる。
やがて入力と出力の位相が合致した。 周波数は341.9Hz だ。
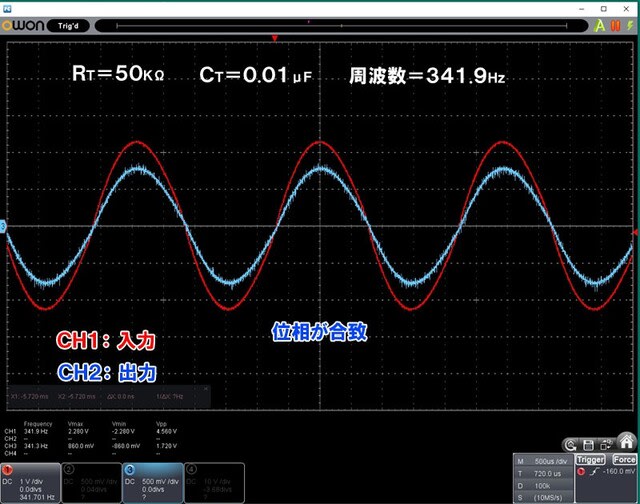
オシロスコープの時間軸を拡大した波形。 波形のピークが一致している。
計算上の周波数は318Hzであるが、CT,RTの誤差や配線の引き回しなどの
影響かもしれない。

周波数を上げて行くと位相は遅れていき、1,429Hzではこんな状況だった。

次にRTを10KΩと小さくして高い周波数で実験してみた。
この場合の計算式での周波数は ≒1.59KHz になったがどうだろうか?
大分低めの171Hzでは大きく進んでいる。

周波数が1,845Hz(1.8KHz)で位相が合った。
計算上では 1.59KHz となったが大体は合っている。

周波数を上げて行くと位相は遅れていき、25KHzではこんなに遅れる。

なるほど、B.P.Fの定数に合致した周波数で出力と入力が同位相になって
その周波数の出力が強め合って出てくるというわけだ。
C(コンデンサ)とR(抵抗)でどうしてサイン波が発振するんだろう?と
不思議に思っていたけれど「位相」の「遅れ」、「合致」、「進み」が作用して
いるんだ。
だけど、どうしてサイン波になるか? 三角波だって、四角波(パルス)だって
出てきてもいいと思うけど・・・オイらのぼんくら頭ではわからない。
これで正弦波発振回路の実験は完結といたします。
いろいろご指導、応援くださった皆様、誠にありがとうございました。
今後ともよろしくお願いいたします。
工作実習生














