致死率が重症化率を上回る ？？？

OGPイメージ

＜新型コロナ＞第6波「致死率」が「重症化率」上回る　医学的には重症なのに…「軽症」扱いで亡くなる高齢者相次ぐ：東京新聞 TOKYO Web

新型コロナウイルスの第６波で、致死率が重症化率を上回る現象が起きている。ワクチン３回目接種が進まず、第５波と比べて免疫が低下した高齢者...

東京新聞 TOKYO Web

 

　昨日の東京新聞のトップ
　新型コロナウイルスの第６波で、致死率が重症化率を上回る現象が起きているという。重症とみなされず、軽症あつかいで、それで死んでいるというのだ。ふざけてる。
　世の中とんでもない状況だと思うのだが、みんなヘーキだ。あきれかえる。
　でもマンボウは延長されるらしいね。それも正しいのかどうかわからない。マンボウなんて無意味とも思うし、解除する状況では断じてない、とも思う。矛盾極まれりだ。心ある為政者は困っているのだろう。

　個人的には市民オーケストラの練習を拒否している。正しい行動かわからない。わからないが、僕はそうしないではいられない。それでも胸が苦しい。オーケストラの練習は、集まって練習する約束をメンバー全員としていることだと思うからだ。
　遠い昔、新婚の頃、こんな台風が来ているのに練習行くのかと言われたが、約束だし、行けるんなら行くと思ったものだ。
　だが、今この状況では練習には行かない。行けない。間違っているかもしれないけれど。
　

オーケストラは素敵だ 茂木大輔

　図書館で借りて再読しようかと思っていたところに古本屋で見つけたのだ。うれしく読み返した。ずいぶん正直に書いてあって好感が持てる。
　1冊目の前半は名著(^^;)「オーケストラ楽器別人間学」の習作？みたいなもので、こちらの方がけれんがなく、むしろオーケストラプレイヤーとしてはなるほどと思えるようなものがある。後半から続にかけては自伝的、音楽エッセイで、すばらしい。

　ドイツでDuを与える（もらった）話がとても印象的だ。
　ドイツ語の2人称は二つあって、「おまえ」である「Du」は上のものが与えるものだというのだ。
　筆者が師匠からおれおまえで呼び合おうと言われるそのちょっとあらたまった、儀式的な様子は感動的だ。

願い事がかないすぎて悲しいこと

　中島みゆきに「悲しいことはいつもある」という曲がある。


　悲しいことなら　いつもある
　願いごとが　叶わなかったり
　願いごとが　叶いすぎたり


　昔、気の置けない男同士で車の中にこの曲が流れ、願いごとが叶いすぎて悲しいってなんだよなあ、そんなことあるかぁ？などと言うから、まあそりゃあ、たとえば、あした天気になれ（という曲もある）と思ったら、何十日も日照りになるとかさあ、と言って、バカ男子集団で、大笑いして、それはそれでいいのだが、本当は違うんだよなあと何十年も思い続けている。


　あそこに、すごーくいい男がいて、好きなのだ。でももう女がいる。それがまたいい女で、それこそ人もうらやむベストカップルなのだ。でもその男が好きなのだ。あんな女って、とても勝てるわけないけれど、事故かなんかで、死んじまって、いや、殺さなくたっていい、男と女なのだ、なにかのきっかけであんな女、っていい人なんだけど、捨てて私の所に来てくれないかと願う。
　願いがかなったら、悲しくない？

うっせぇわ のこと

「うっせぇわ」は、つまり中島みゆきの女なんてものにと同じものだ。
　詩というのは歌詞でも、意味がなくては。それは「誰もが感じているけれど言葉にできてない」ことをことばにすること、だと思うのだ。
　だから「うっせぇわ」は、これだけうけた。若いもん（おんなは、自分以外）は今までの苦労を引き受けろ、世の中こうなってる。そんなの「うっせぇわ」。
　じつは女なんてものにのほうはさらに深くて、こっちは、悲しいのはわかるけど「忘れてみれば？」「笑ってみれば？」。でも（なぐさめはわかるけど）「笑ってもあなたは帰ってこない」と言うのだ。今の自分にとっての理不尽が、本当の真実が、言葉になっている。
　がんばったけどダメだけど、でももう一回がんばろう、やっぱりダメだけど1番じゃなくても良い、あんたがんばったね。そのままで良い。ちまたはそんな歌ばっか。そうかと思うと、自分が出たんでもないのに、金メダルとれなかった、努力が足りない。ほんとバッカじゃなかろうか。

　→傘がないのことも

2月23日は中島みゆきの誕生日

　そんでもって、2月23日は中島みゆきの誕生日だ。
　中島みゆきは高校の予餞会に来たのだ！すごい。当時の生徒会、すごいなあ。（こんなこと書くとすっかりバレる？）
　感動してねえ。以来ファンである。

　中島みゆきのすばらしさは、もちろんそのすべてなのだが、特に歌詞だよなあ。たしか卒業研究は谷川俊太郎だったというのを、なるほどと思ったものだ。
　最近のと言うか、もう何十年も、うすっぺらい前向きソングばかりの中で、気づかないでいる本質を見せてくれるのが中島みゆきだと思うのだ。
　少なくともぼくは「女なんてものに」が原点だと思っていて、その、誰がなんと言おうともぶれない本質を突いていると思う。
　ぼくが何を書いても意味はない。最近聴いてない。たまには昔を思い出すか。

２月２２日は猫の日らしい

　２月２２日は猫の日らしい。なんだそりゃ。

今日買った古本

　今日買った古本。読むのが楽しみだ。

　市役所に行こうとしたのだが、21日で月曜だったからだろう、駐車場に入るのに行列なのだ。すごすごと帰って来た。いや、そうだ種芋を買おうとホームセンターに行ったのだが、今年（去年？）はジャガイモがとても不作だったらしく、ロクなのがない。キタアカリのすごーく小さい種芋を買ってきた。高かった。しょうがない、小さいのを大きく育てられるかな?がんばるぞ。

禍の科学 ポール・A・オフィット

　なかなかおもしろかった。知らなかったこともたくさんあった。だが、この著者の姿勢も自分自身が非難しているようなものだと思う。ずいぶんたくさん断定的に書いてあるが、将来それは違うと言われる可能性があると思う。
　たとえば環境ホルモン、DDTやビスフェノールAのことが無害だ、あるいは安全だと書いてあるが、ごく微量、低濃度の、環境や健康に与える影響を過小評価していると思う。、遺伝子操作は普通の品種改良と同じだと書いてあるが、そんなことはないと思う。
　たとえばフロンのように、それはいまだに直接的には無害な物質だろう。だがそれは思わぬ影響を地球規模で与えることになった。
　所詮、この著者も自分が非難するように、時代の空気に流されている。いや積極的に乗っている、と思う。
　じゃあお前は？といわれれば、返す言葉はない。長い歴史の中で、科学は万能ではない、わからないことが多すぎる、多くのことが、断定できない、ということがあきらかになった、としか言いようがない。

節分きびだんご

　コロナのせいで人には会えないし、次女も今年はバレンタインのチョコをばらまけなかった。
　時季外れのきびだんごが悲しい。気分が晴れない。

イチゴプリン

　なんだかイチゴが評判の店のものらしいが、プリンになってしまうとただおいしいだけだなあ。おいしい。

　来年度の仕事のことがどうなるか気を揉んでいる。まだ二月だ。気になって実に良くない精神状態だなあ。それほどでもないか。ともかく得意分野で能力を発揮させてもらいたいものだ。
　気に病んでいるせいか、ただの老人だからなのか、ますます早起きになっている。それはまあいいか。ひとと生活時間がずれているというほどでもないのだが、楽器触る時間がなくてまいる。いや、テレビ見たり、ネットで碁を打ったりしている。いかんなあ。

ボワモルティエ作品27 からソナタ1番 ハ長調

　アルマンド、クーラント、ロンド-、ジーグの4楽章
　ヴォイスフルートで吹いたので三度下（でバロックピッチ）で吹いた。実にたいしたことない。ハ長調だし。ジーグの後半、息がもたない。どうすりゃあいいんだ。とても保たない。通奏低音と打ち合わせして、どこかで息を継ぐ時間をもらうのが良いかもしれないなあ。

居間のラックの上だけちょっときれい

　家じゅうちらかりきっていて、とても人は呼べない。まあ、妻も呼ぶ気もないのだろう。こんなことでいいのか。
　むかし洗面所のドライフラワーの写真を撮ったらちょっと良かった。（→ドライフラワー）居間のラックの上の写真を撮ったら、これだけなら他人に見せても良いか。

ブラックホール

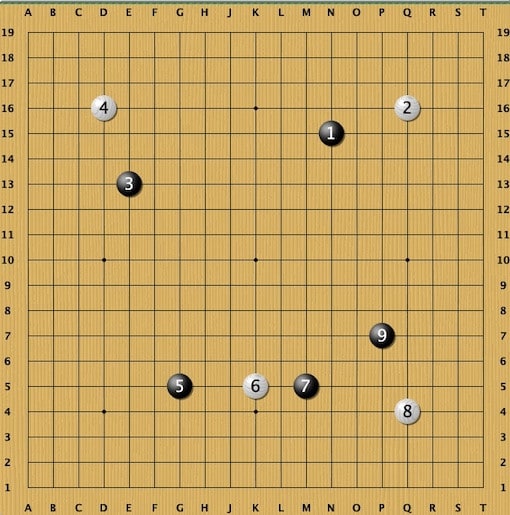　図と手順は違うが、1359の4手をブラックホールというらしい。張栩がNHKでやったのを初めて見たときは狂喜乱舞したものだ。今回は6に入ってきたもので7に8と星に打ったので3−3に入って取れちゃった。すごい。うれしい。

よつばと！ あずまきよひこ

　同僚が貸してくれた。職場で何人も借りていて空前の漫画ブームである。(^^;)

　おとな買いしたのだろう、この箱がダンボーで、すばらしい。
　僕も買ってひまひまに、あるいはトイレに置いてどれか1話2話、読むものかと思ったのだが、なんかひやひやしちゃってね。つまり交通事故が怖い。誘拐されそうだ。気球から落ちちゃうんじゃないか。すくなくとももう前歯はかけて、ないと思う。(-_-;)

　僕の次女は2階から落ちて大腿骨を折った。スケートで転んで腕も折った。こわい。

　そういうわけで、平常心で読めない。
　どうにも、少なくとも僕は、汚れちまった現代に生きているんだと思う。

対数のこと （ちょっと改訂 再掲、2008.12.8)

　恥ずかしながら（ん？）、中学生の時、理科部に所属していた。でも全然研究活動みたいなことをやったおぼえがない。たまに理科室に行ったことはあるけれど、ぐずぐずしていたんだろう。
　印象的に覚えているのは、先輩たちが（って、自分たちじゃないところが情けない）浮き草（たんぼにうかんでるやつね）の研究をしていて、そのまとめをしていたときのことだ。
　個体？というか、葉っぱの数がだんだん増えていく。グラフにすると右上がり、傾きがだんだん大きくなる。「グラフから、増える速度がだんだん大きくなるのがわかります。」というのだ。そうかなあ、必ずしも、そうは言い切れないんじゃないだろうか？たとえば、1枚が2枚、4枚、8枚、、、、と来て、次が14枚だったら（2倍になるなら16枚のはずだから）増え方は減ってるはずですよねえ、でもグラフは同じような感じじゃあないですか。（グラフ参照）そのグラフからだけでは、必ずしもそう（増え方が増していると）は言えないんじゃあないですかねえ？
　自分でやってるのでもないのに偉そうに言う下級生に対して、先輩は、ほんとだ、そうだよねえ、と納得してくれて、今考えるといい先輩、いい部の雰囲気だったんだなあ。でも中学生の頭ではそれ以上のことはわからなくて、どうまとめたかも忘れてしまった。
　高校に入って、対数を習って、感激した。そうか、曲線状になる、1.2.4.8.16と言う変化を直線状にするという機能を対数というのは持っているんだ！
Log2( 2 ) = 1
Log2( 4 ) = 2
Log2( 8 ) = 3
　となり、
Log2( 14 ) = 3.807354922
　であり、
Log2( 16 ) = 4
　より小さくなる。
　グラフにすれば、14のところで増加速度が落ちているのがわかる。(上のグラフの赤線)
　後で知った片対数のグラフ用紙もすばらしい。
　でも数学の授業は、対数を技術的に扱う（計算する）ことに終始して、全然おもしろくないし、ろくにできるようにならなかった。