平成２６年１月２６日（日） 
本当に先週水曜日から日中は、あたたかい１５℃にも気温上昇。
朝方は、逆に零下に近く気温が下がり、所謂放射冷却現象とも言われています。
子どもたちは、戸外で元気に遊んでいます。
『こどもは風の子、おとなは火の子』
と、昔から言われています。
冬でも九州では、外遊び中でも、寒さにも肌を晒して、
「風が冷たい。」と感じながら遊ぶことが、
自律神経系の発達のためにも大事なのです。
そこで、この時期の外遊びの代表選手の一つである
『なわとび』について本日は少し述べさせていただきます。
東京の白梅女子短期大学の無藤隆先生の以下のご持論
実に興味深いお話が、Ｆａｃｅｂｏｏｋでも展開されています。
縄跳びで数えることは、数の発達と関連する。
縄跳び（特に大縄跳び）を 幼児がしているのを見ていると、
「数の発達」を垣間見せてくれます。
跳ぶたびに、「１」、「２」、「３」と 跳んだ数を数えます。
それは、「数えなさい。」とは強要されなくても
自然に自発的に子どもたちは楽しそうに数えます。
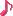
その『数唱の練習』という「ねらい」や「目的」を超えて、
楽しみながら大きい声で数えるのです。
第一に、『離散量』を『連続量』につなぐことです。
数えるのは『離散量の集合数』についてです。
コマを回す時間を数えるとすれば、それは
『連続量』を『自然数』で数えることです。
縄跳びは、動きは連続しますが、
第一は、循環をなす動きの単位があり、
しかも地面をたたく音によりその単位が判別されます。
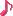
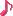
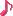
第二に、『集合数』と『順序数』のはざまにあります。
どこまで行ったかを数えるというのは「順序」についてです。
しかし、全体の量を表すという意味では「集合」についてです。
第三に、跳ぶのを数えるのは、
常にその先に行こうとすることが意図されているのです。
力の限り子どもは飛び続けようとしますが、
その続く営みを、「数」は、いわば 同伴します。
「数」は先へと延びていき、縄を飛ぶのは「無限」に続くようです。
「数」の延長可能性を感じさせるようです。
飛ぶのが終わるのは 「数」が終わるのではなく、
実はもっと先まで力があれば飛べるように「数」もまた先へと続きます。
（いずれいくらでも数えられるという意味での『無限の概念の発見』に行き着くはずです。）
第四に、例えば、「１」と「２」の間のつながりが体の実際の動きとしてあり、
だから連続量になっていくのですが、その始まりは、
「離散の量の間、実在する何かがある」
という感覚が形成されること
によって可能になります。
それはいずれ数直線の考えとなっていき、
小学校算数の骨格を作ります。
だからといって、縄跳びをすると、
直ぐに数の理解が増すというのではないでしょう。
ただ、そういった数に絡む活動がたくさんあれば、数理解が増し、
小学校以降の算数の基礎が形成されることがありそうです。
例えば、ぶらんこ遊びの場合も、１０回ずつこいだらお友だちと交代する
というような遊びのルールがあれば、ぶらんこが一往復するたびに
「１！」・「２！」と数えて～「９！」「１０！」までの数唱の繰り返しで、
時間の経過と「１～１０」の数の持つ意味が同時的に身に付くようです。
だが、まだ実証研究はちゃんとしたものはありません。
マラソンごっこやボール遊びでも、鬼ごっこでも、
そのような数量概念の形成と結びついている場面が見られるのかもしれません。
ちなみに、上記のような分析は、近年、
アメリカのジョージ・レイコフは、
認知言語学の創設者の一人であり、特に、従来文章技巧の問題として
言語学からは周辺的な現象として扱われてきたメタファーを、
日常の言語活動に必須の認知能力（概念メタファー）として
捉え直したことで有名です。
レイコフは1980年、哲学者マーク・ジョンソンとの共著Metaphors We Live Byで、
「議論は戦争である」「良いことは上である」「考えは食べ物である」
などのメタファーのパターンが,日常言語に溢れていることを指摘しました。
レイコフはここから発展して、
人間の抽象的な概念能力は、
経験に基づいた具体的・身体的な認知機構からの
メタファー的拡張によって可能になっていると主張し、
心身二元論に基づいた西洋哲学の伝統に対する批判を行っています。
日本語の翻訳も最近出ています。
この時期は、ご家庭でも大いに『なわとび』 、
そして、
『ボール遊び』や、『鬼ごっこ』でも楽しく遊びをとおして
数概念を発達させましょう！
成長をお祈りしています。
