３次方程式のガロア理論(中盤)〜エヴァリスト･ガロアを巡る旅､その１１

　前回”その10”では､群があみだクジや図形の対称性と密な繋がりを持つ事を長々と紹介しました。
　というのも､対称性とそれが生み出す群は物質の対称性を理解する上で､今では貴重なツールとなるものです。
　特に､鏡像を作る対称操作は私たちの生活に深い関わりを持ちます。それは､人工的に作られた化学物質では鏡像の構成や配列が同じでも､全く別の物質になるからです。
　代表的な例が人工甘味料ですが､この性質を使い､甘みを感じるが身体には吸収されない。
　何だか､気味悪い物質ですが､日常にあふれる化学物質が群の性質を使い､次々と作られ､同時に生物の遺伝子構造や物質の結晶構造が次々と明らかにされていくんですね。

　そこで今日は､対称性の表現としての群と部分群について述べたいと思います。
　群の3つの条件として､”繋げる”･”変えない事が出来る”･”元に戻せる”を挙げました。そして､群が図形の対称性と深い関わりを持つ事でした。

部分群とは

　この対称性を理解するには､群の内部構造を分析する必要がある。そこで､群の内部にある”部分群”と呼ばれるものを扱います。
　まず､どんな群Gにも明らかな部分群がある。それは､群Gそのものと単位元eのみからなる最小の群{e}です。
　例えば､Gを整数の集合とし､足し算を演算とすれば､{0}はGの部分群になる。また､Nを全ての偶数とすれば､足し算にて閉じ､単位元(0)と逆元(xに対し−x)はNに含まれ､整数の加法群Gの部分群だと解ります。
　しかし､Nを自然数の集合とすれば､加法に対し単位元(0)と逆元(−n)は存在せず､部分群にはならない。故に､整数の全てはGの部分群になるが､整数の中から取り出した自然数の集合はGの部分群にはなりません。
　つまり､群Gの中の元を取り出して作った集合Nが､Gと同じ演算に対し群を構成してれば､”NはGの部分群”となります。

　そこで､正方形の対称操作の群Gの部分群を全て見つけます。
　前回”その10”でも述べた様に､正方形の対称操作には､線対称(反転)操作のヨコ軸･タテ軸･左斜め軸･右斜め軸の計4つ(S₁,S₂,S₃,S₄)と､それに回転の対称操作は反時計回りに90度･180度･270度の3つ(R₁,R₂,R₃)と､”何もしない操作”eを含め､合計で8つの対称操作がありました。
　Gの元同士の”対称操作を繋ぐ”という演算※の数は､8×8=64通りでしたね。
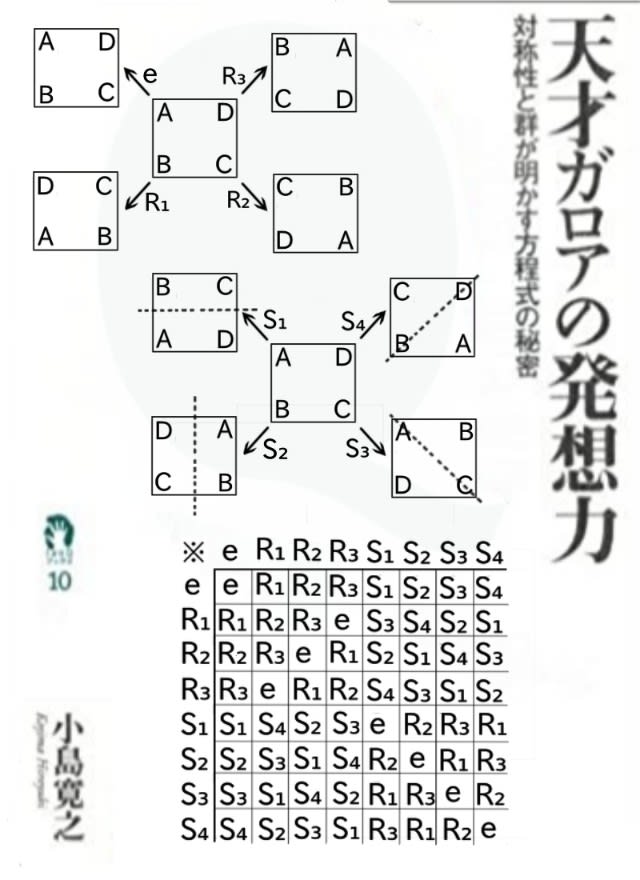
　そこで､乗積表を作れば冒頭のイラスト(下部)の様になります。
　但し､正方形の頂点ABCDは反時計回りに配置し､e:ABCD→ABCD､R₁:ABCD→DABC､R₂:ABCD→CDAB､R₃:ABCD→BCDA。S₁:ABCD→DABC､S₂:ABCD→DCAB､S₃:ABCD→ADCB､S₄:ABCD→CBDA､とします(イラスト上部参照)。
　少し面倒ですが､イラストの表を眺め､Gの全ての部分群を抽出します。

　まず明らかな部分群は､G自身と単位元のみの{e}でした。それに加え､回転対称操作のみの集合{e,R₁,R₂,R₃}ー①です。
　表の最初の”4×4マス”を見れば明らかですが､全てが回転対称操作Rの要素ですね。 　
　次に､部分群は必ず単位元eを含む必要があるので､eに何か1つ元を加えた2個の元からなる部分群を考えます。
　まず気付くのが{e,S₁}ー②。S₁※S₁=eでS₁それ自身が逆元となるが故に､{e,S₁}は部分群です。同様に､これとそっくり(同型)な部分群は､{e,S₂}ー③､{e,S₃}ー④､{e,S₄}ー⑤となる。
　これら4つの部分群は”裏返しの裏返しは元のまま”という群ですね。乗積表で見れば､対角軸に対称となります。

　次に､eに回転対称操作Rを1つだけ加えて部分群に出来ないものか？
　180度の回転操作R₂で､{e,R₂}ー⑥だけが部分群になります。乗積表で確かめれば､{e,S₁}と同型ですね。
　以上で､群Gそのものと{e}を含めた①②③④⑤⑥の合計8個の部分群が見つかった訳ですが､他にはないのだろうか？

　そこで､群Gそのものを除く7つの部分群は可換(対角軸に関して対称)になってるので､それらを乗積表から探し出します。
　すると､労力のいる作業ですが､{e,R₂,S₁,S₂}ー⑦と{e,R₂,S₃,S₄}ー⑧の2つの集合を発見できます。この集合の乗積表で見れば､2つが同型の部分群である事も確認できますね。
　故に､群Gそのものと{e}も含め､計10個の部分群が発見できました。

巡回群という特殊な群

　しかし､もっと効率のいい見つけ方はないのか？
　実はある種の群は､1つの元を特定し､その元を演算し続け､簡単に見つける事が出来る。例えば､R₁を繰り返し演算すると4回目にはeになり､5回目には1周してR₁に戻る。
　R₁※R₁=R₂､R₁※R₁※R₁=R₃､R₁※R₁※R₁※R₁=e､R₁※R₁※R₁※R₁※R₁=R₁の繰り返しである。
　この様にして､上述した{e,R₁,R₂,R₃}の群を見つける事が出来る。この様に､1つの演算を何度も繰り返す事で得られる群を”巡回群”と呼びます。
　つまり､部分群を探す時は､まずこの巡回群を列挙する必要がある。

　そこでS₁に対し､同様の事を行えば､S₁※S₁=eから巡回群{e,S₁}が得られる。この様に巡回群を作る事で､上で述べた最初の7個の群(可換群)が簡単に発見できますね。
　しかし､群Gそのものと最後で求めた{e,R₂,S₁,S₂}と{e,R₂,S₃,S₄}の2つの部分群は巡回群ではない。
　では､巡回群ではない部分群はどうやって見つけるのか？
　これこそがガロア理論の中核をなし､部分群が図形の対称性と蜜な繋りがある事の重要なヒントなんです。

　そこで､10個の部分群の”家系図”を分析してみます。
　例えば､②③⑥はGの部分群であるだけでなく､⑦の部分群でもある。こうした関係を”ハッセ図”という家系図で書き出します。
Gー{e,R₂,S₁,S₂}ー{e,S₁}{e,S₂}{e,R₂}ー{e}
　  {e,R₁,R₂,R₃}ー{e,R₂}ー{e}
 　 {e,R₂,S₃,S₄}ー{e,S₃}{e,S₄}{e,R₂}ー{e}
　これを番号で表せば､
G→⑦→②③⑥→e
　  ①→⑥→e
　  ⑧→④⑤⑥→e､と簡単になります。
　因みに､左側の部分群が右側の部分群を含む事を示してますね。
　(注)イラストの挿入が上手くいかないので､この図で勘弁をです。

ハッセ図という家系図

　そこで､群Gは”正方形を自身に重ねる対称操作の全て”だから､群Gの部分群Nも”四角形Xを自身に重ねる対称操作の全て”と想像出来ますね。　　
　部分群Nが{e}の時は､”何もしない”操作だから､四角形Xは全ての四角形となる。
　次に､部分群Nが{e,S₃}の時､S₃は”ACに関する線対称”だから､正方形だけでなくタコ形も含む。
　この様に､部分群として群を小さくすれば､その群に含まれる対称操作で不変となる四角形の世界は逆に広がるんですね。

　同様に､部分群{e,S₁}が描く四角形Xは”辺ADと辺BCが等脚な台形の集合”となる。また､部分群{e,R₂}が描く四角形Xは”平行四辺形の集合”となります。180度の回転操作で自身に重なる図形が平行四辺形なのは明らかですね。
　更に､部分群{e,R₂,S₁,S₂}が描く四角形は”長方形の集合”です。長方形は大変の中点を結ぶ線に対し線対称であり､対角線の交点を対称点とする点対称だからです。
　また､部分群{e,R₂,S₃,S₄}の描く四角形は”ヒシ形の集合”です。ヒシ形は両方の対角線に対する線対称性を持ち､更に点対称ですね。
　故に､これらの部分群から四角形を描く事は､”その部分群がどんな対称性を表現するのか？”に依存すると言える。
　少し混乱しそうですが､これをハッセ図(家系図)で書いてみましょう。

四角形{e}ーAD=BCの等脚台形{e,S₁}②
　　　　 ーAB=CDの等脚台形{e,S₂}③
　　　　 ー平行四辺形{e,R₂}⑥
　　　　 ーACが軸のたこ形{e,S₃}④　
　　　　 ーBDが軸のたこ形{e,S₄}⑤
②③⑥ー長方形{e,R₂,S₁,S₂}⑦ー正方形G
⑥ー正方形{e,R₁,R₂,R₃}①ー正方形G
④⑤⑥ーひし形{e,R₂,S₃,S₄}⑧ー正方形G
と､家系図は全く逆となる。
　これも､番号で簡略化すれば､
四角形e→②③⑥→長方形⑦→正方形G
　　　  →⑥→正方形①→正方形G
　　　  →④⑤⑥→ひし形⑧→正方形G　　
となる。ハッセ図とは程遠いですが､ご勘弁をです。
　つまり､群が小さくなる程に群が描く四角形の集合は大きくなりますね。

　部分群を見つけるのは難しいが､群が描く四角形から逆算して部分群を見つければ？と勘のいい人は思ったでしょう。
　そう､数学はセンスが物を言う学問でもあるんですね。
　例えば､ひし形の対称性に注目し､ひし形を不変にするGの元を探りだせば､ひし形の対称性から{e,R₂,S₃,S₄}はすぐに見つかります。
　これは､”群のハッセ図”と”群が描く図形のハッセ図”がピタリと対応してる事を示唆してます。この発想こそが､ガロアのアイデアの中核をなします。
　言い換えれば､”自己同型の群のハッセ図”と”群が描く代数体のハッセ図”がピタリと対応する。
　ガロアはこの対応を利用し､”方程式が四則とルートで解けるか？”という代数体に対するハッセ図を､ある種の部分群に対するハッセ図にそのまますり替える事が出来る事に気づいたのです。

　つまりガロアは､”部分群のハッセ図から､群が描く代数体のあり方”を特定するという逆方向の道を歩んだんです。
　これは､ペレルマンがリッチフローを逆行させ､ポアンカレ予想を解決した手法と同じですね。

　以上､長くなったので､ここまでです。
　次回は､部分群の元の個数と正規部分群について述べたいと思います。この正規部分群こそが”体の自己同型をなす群”と大きく関わってくるんですね。