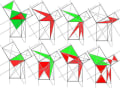
・・・「ピタゴラスイツチ」・・・「比他語等諏一致」・・・「比的額羅斯(Pythagorean)の定理(Theorem)」・・・面積が同じで形が異なる「三角形」での証明・・・漢字字形が同じで意味が異なる漢字・・・音声が同じで意味が異なるコトバ・・・「比的額羅斯」って、「比べる的(まと)は額(ひたい)の羅(あみ)の斯」・・・別の漢字の宛て名は「龐太我剌私 (ピタゴラス)」であるらしいが、これなら、「龐(䮾=馬+龍・龎=厂+龍)の太、我は、剌す私(ム・邪・よこしま・横嶋)=邪まな奴を刺す」である・・・「ピタゴラス」ではなく、
ーーーーー
「龐」とは「龐涓(ホウケン)」の示唆だろう・・・
「龐」の異字漢字は
䮾=馬+龍
龎=厂+龍
で、「おおきい・みだれる・ホウ・ボウ・ロウ」の音訓である・・・
意味は、
「高い家屋・高大、
厖・尨と通じ、
乱れ雑った様子」
「充実した」
「高屋なり(説文解字・巻九)」とあるらしい・・・
・・・字形「䮾=馬+龍」なら「坂本龍馬」である・・・
熟語に
龐錯=みだれる・入り乱れる・乱雑
龐大=数量的表現の膨大、厖大
龐眉皓髪=尨眉皓髪・髪や眉に白い毛が混じる
龐龐=ボウボウなっている容貌・・・茫々
人物名
↓↑
龐会(?)三国時代の曹魏の武将。龐徳の子
龐羲(?)後漢末の武将
龐涓(?)中国戦国時代の魏の武将
龐煖(?)春秋戦国時代の趙の武将
龐統(178年?~213年?)後漢末の武将、政治家
龐徳(?~219年)後漢末の武将
龐萌(?~30年)新代から後漢初にかけての武将
↓↑
・・・知っているのは「友人(孫臏)の足を切断」した「龐涓」だが・・・
魏の人物で
「龐涓」は
斉の
「孫臏(ソンピン)」
と共に
「鬼谷子」に兵法を学んだ親友
魏の国戻って
「魏恵王(魏罃)」に仕えた
龐涓(ホウ涓)は将軍になり
「孫臏」を魏に招き
魏への仕官が出来るようにと
その滞在中に
孫臏を罠に嵌め、
孫臏の両足を切断
顔に黥(刺青)され
龐涓の家に軟禁された
斉の将軍
「田忌」が魏を訪れ
孫臏は密かに田忌と面会し、
田忌の車に隠れて魏を脱出・・・
魏が趙の国を攻撃した際に、
趙の援軍で
将軍田忌
軍師の孫臏
が
魏の国都
大梁に向かい
魏軍を破った(桂陵の戦い)
紀元前341年
斉軍に敗れた魏に対して
韓国が攻めたが
魏と五度戦って五度敗れ、
斉に援軍を求めた
斉は
田忌と孫臏(孫ピン)を援軍を送り
魏の国都大梁に向かった為、
韓に攻め込んでいた太子の
魏申は軍を引き返し
斉軍を攻撃
退却した兵の竈を減らしていった
斉軍を
龐涓(ホウ涓)は、
歩兵を残して
騎兵のみで追撃したが
退却は孫臏の罠で
魏軍の追撃軍を、
道の狭い馬陵の地誘い込み
馬陵の地に現れた
龐涓(ホウ涓)は、
暗がりの中で
皮を削られて
木を見つけ、そこには
「龐涓、この樹の下に死せん」
記されていた
孫臏の伏兵が
龐涓の灯りめがけて矢を射かけ
魏軍は大混乱
龐涓(ホウ涓)は、
「遂に豎子(若造・青二才)に名を成せり」
と云って自害・・・
・・・ここには「龐涓」の
「龐(乱れる)=广+龍・厂+龍
厖=厂+尤+彡
尤=とが・罪科・もっとも
甚だしい・ユウ
彡=毛羽痕
「涓(ちょろちょろ流れる水・小川の細流
わずかなこと・小さいこと
滴(雫・しずく)が落ちる様子)」
の意味が語られているだろう・・・
↓↑
で、「ピタゴラス経団」で「アルケーは数である」とし
「男は3、女は2、その和5が結婚」、
「シンボルマークは五芒星」、
「五芒星の比率が無理数であったことを
洩らした教団員を溺死させた」、
「クロトンの家にいる時に放火されて、逃げ出し、
豆畑まで立ち止まり、追手に捕らえられて
咽喉を切られて殺された」
ピタゴラスか?
刺客に襲われ頭蓋骨、眉間を切られて殺された
坂本龍馬か・・・?
兎に角、「龐太我剌私」で「比的額羅斯」・・・まさか「瀧廉太郎」じゃぁないだろう・・・「荒城の月」、ピアノ曲「憾(うら)み」って・・・?・・・漢字はが似ているのは「朧月夜(おぼろづきよ)」、「作曲は岡野貞一、作詞は高野辰之による日本の唱歌。1914(大正三)年・尋常小学唱歌・第六学年用に初めて掲載」・・・デスか・・・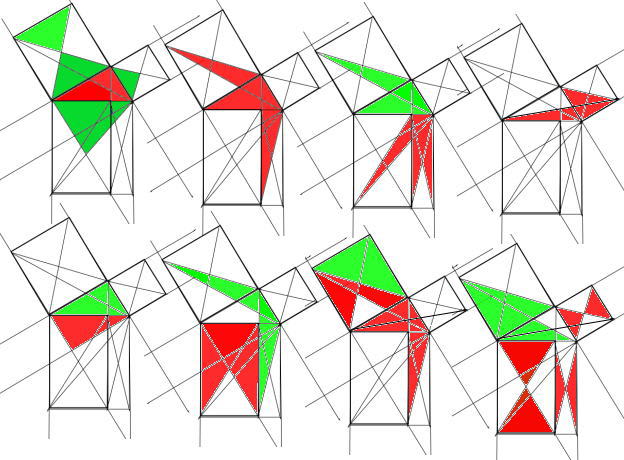
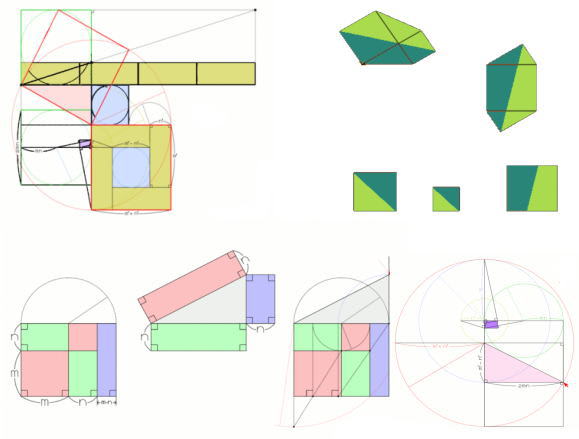
↓↑
↓↑
ピタゴラスの定理
(Pythagorean Theorem)
c²=a²+b²
「鉤股弦法(コウコゲンホウ)」
↓↑
古代中国の数学では
鉤股弦(コウコゲン)法
古代の数学書
『周髀算経』
『九章算術』
に記述
日本でも「鉤股弦」の漢字を使用
鉤は「かぎの手」で直角を挟む短辺
股は「足の分かれめ」で長辺
弦は「弓のつる」で斜辺
↓↑
勾股定理=商高定理=鉤股弦法
三平方の定理
3,4,5の直角三角形
3²+4²=5²
↓↑
n=1,2,3...とすると
(3,4,5)(6,8,10)(9,12,15)...
ピタゴラス数が得られる
(5,12,13)は
どんなnからも不可能・・・
(5,12,13)は
a=2n+1、
b=2n(n+1)、
c=2n2+2n+1
とした時の
「n=2」の場合で、
任意の
自然数nについて
(2n+1)2+{2n(n+1)}2
=4n4+8n3+8n2+4n+1
=(2n2+2n+1)2
(a,b,c)のピタゴラス数となる
ーーーーー
・・・ここ、北海道も「ナツ、ッ」って、カンジである・・・