３次方程式のガロア理論(前半)〜エヴァリスト･ガロアを巡る旅､その１０

　前後2話で9千字近くを掛けて､ご丁寧に紹介した2次方程式のガロア理論でしたが。3次方程式のガロア理論に関しては､少しややこしくなるので､3回(前半･中盤･後半)に分けて紹介したいと思います。
　但し､最後でも述べますが､群論を完璧に理解してる人は､この記事は必要ないかもですが､”群を対称性で捉える”という事こそがガロア理論の中核をなすので､読んで損はないと思います。

　3次方程式も同様に､方程式の解から作る代数体の自己同型の仕組みを見破る事で解の公式を明らかに出来ます。
　結論から言えば､まず3次方程式の解を全て加えた体を考えます。ここでは､有理数体Qではなく､1の3乗根ω(x³=1の複素数解)を有理数体に加えた体F=Q(ω)を基礎体とし､Fの拡大体Kを考えます。
　Kの自己同型は一般に6つありますが､これは3次方程式の3つ解の置換の順列組合せが6(=3!)事から来てますね。
　以下でも述べますが､ガロア群は､3つの元(解)を置き換える置換となるからです。
　この6つの自己同型の作る群Gは､三角形の自身に被さる対称操作(線対称と回転対称の6通り)の群と同類です。3本のアミダくじをイメージした方が判り易いですね。

　これも以下でも述べますが､この群は3つの元からなる部分群Hで巡回群なるものが存在します。そして､G→H→e(自明な部分群)がF=Q(ω)→M→Kに対応する”(ハッゼ)図”が出来上がります。
　体Mは体Fを拡大したもので､Q(ω)にある数の平方根を加えた体がMとなる。更に､このMにある数の3乗根(立方根)を加えた体がKである事が判明する。
　結果､有理数と1の3乗根ωの四則演算と平方根(√)と3乗根により､体Kの数は全て”表現”できる事が解る。
　ガロア群を”ガロア表現”と呼ぶのも､少しは頷けますね。

　そこで､2次元方程式と同様に､3次方程式の解の作る代数体の自己同型へと話を進めたいのですが､群とωを理解しないと先へは一歩も進めないので､まずは群論の説明からです。
　｢天才ガロアの発想力｣の著者小島寛之氏も言われてる様に､中学生でも理解できる様なレベルなので､リラックスして読んでください。

群とアミダくじの関係

　”今更聞けない？群と体と環の関係”でも述べましたが､やはりイマイチ解らないという人が多いと思います(悲)。
　そこで､ガロア理論の視点(自己同型)から群を振り返ってみます。

　前々回”その8”でも述べた様に､2次方程式の解から作る自己同型は”恒等写像”と解の入れ替え(置換)の”共役写像”の2つだけでした。
　そして､共役写像の”解の入れ替え”を2つ繋ぐと恒等写像になります。つまり､共役写像を2つ繋げば元に戻り､群の構造を提示します。

　群とは一言で言えば､”動きや変化”の代数学です。動く(変化する)対象物があれば､動きや変化を繋ぎ合わせ､連続させる事が出来る。
　そこで2つの動きや変化を繋ぎ､1つにする時､四則演算が代数計算であると同様に､この動きの繋ぎ合せも特有の計算となります。
　これこそが群の概念です。
　故に､前述した様に､”2個の対象物の入れ替え”は､容易に群の構造を持つのです。

　群の誕生は方程式の解の”置き換え”が起源で､ラグランジュに始まり､アーベルの発見を促し､更にガロアは群を使い､方程式の解の構造を明らかにします。
　つまり群論とは､方程式の解の研究から始まったものと言えますね。

　2次元方程式では対象物は僅かに2つでしたが､3つあればどうなるのでしょうか？
　そこで3本のアミダくじを例にとります。
　始点をKQJとすると､アミダくじの終点は(KQJ､KJQ､QKJ､QJK､JKQ､JQK)6通りですね。
　ここで､τ:KQJ→JKQとθ:KQJ→QKJとなるアミダを例にします。すると､τとθを経由したアミダはKJQに到達する。この動きをσ:KQJ→KJQとすれば､演算記号※を使い､τ※θ=σと書けます。
　そこで､3本のアミダの集合をAと書き､Aに属する個々のアミダくじ(計6種類)をf､g､h･･･とし､fの下にgを繋いだアミダくじをf※gと記せば､①f※gはAに属するアミダくじですね(演算※にて閉じる)。②h※(g※f)=(h※g)※fですが､これはh※(g※f)も(h※g)※fもf,g,hを順に繋いだアミダに変わりはないという事です。
　これこそが”結合法則”と呼ばれる代数法則です。
　ここで注意ですが､一般にアミダの演算の組合せでは､”交換法則”が成立しません。τ※θ:KQJ→KJQでしたがθ※τ:KQJ→とJQKと一致しないからです。
　一方､素アミダ(縦棒のみ)をeとすれば､③f※e=e※f=fが成立し､このeを”単位元”と呼ぶ。また､④f※g=g※f=eなるgが存在し､このgを”逆元”と呼びます。
　この単位元と逆元は､e=1と数字に置き換え､※を掛け算とすれば､理解しやすいですね。f×g=g×f=1で､逆元は逆数(1/g)を表します。
　故に､素アミダe(単位元)に対し､逆元はアミダくじを裏返しにした逆アミダになる。
　

有限群と可換群

　このアミダくじの代数世界の法則こそが群であり､群Gの要素をf､g､h･･･とすれば､群の定義は①演算※について閉じてる②結合法則{h※(g※f)=(h※g)※f}③単位元e{f※e=e※f=e}の存在④逆元gの存在{f※g=g※f=e}の4つとなります。
　つまり､群とは①繋げる②変えない事が出来る③元に戻せるの､3つの条件を満たす世界なんですね。
　そこで､整数の集合をZとすると､Zは足し算に対し群となる。単位元は0(0+x=x+0=0)で､xの逆元は−xは明らかですね。
　一方で､有理数Qから0を除いたものをQ’とすれば､Q’は掛け算に対し群となる。単位元は1(1×x=x×1=1)で､xの逆元は1/xですね。0を除くのは0が(掛け算での)逆元を持たないからです。

　上述した様に､ガロアによって19世紀に導入された群ですが。ガロアは5次以上の方程式に解の公式がない事を証明する為に､体の自己同型を作る群を分析します。
　そこで､この自己同型を作る群こそがアミダくじの群と同じものです。
　この”動く代数学”と呼ばれる群を十分に理解する為に､有限群と可換群を理解する必要があります。

　ここでは､その例を幾つかあげます。
　まず最も単純な群ですが､G={0}で演算は足し算(+)。計算は0+0=0のみですが､立派な群です。
　次に､G={+1,−1}で演算は掛け算(×)ですが､答えは+1,−1のみで掛け算で閉じてる事は明らかです。単位元は+1で逆元は+1の時は+1､−1の時は−1。群の乗積表を作ると解り易いです。因みに､上の2つの例は有限群ですね。
　3つ目は､G={偶数,奇数}で足し算(+)で閉じてます。結合法則は明らかですが､単位元は偶数+偶数=偶数､奇数+奇数=偶数により偶数です。また偶数の逆元は偶数+偶数(単位元)=偶数により偶数で､奇数の逆元は奇数+奇数(単位元)=奇数により奇数ですね。これも上の乗積表を作ると解り易いです。
　勘のいい人なら､2番目と3番目の群は構造が同じと気づいたでしょうね。
　{+1,−1}→{偶数,奇数}､×→+という対応ですから､対象物と演算の見た目は違うが､群としては同じ構造になってる。

　実は､2次方程式の無理数解αを有理数に加えて作った2次体Q(α)の自己同型は群となります。
　そこで､この様な自己同型の恒等写像をe(x)とし､解αを解βに対応させる共役写像をf(x)とします。
　e(f(x))=e※f､f(e(x))=f※eという演算※を考えると､e(e(x))=e※e､f(f(x))=f※fという写像の合成が定義できます。
　eは恒等写像より､e※f=f※e=f､e※e=eは明らかで､冒頭で述べた様にf※f=eですね。そこで乗積表をつくれば､例2と例3の群と同類な事が判ります。
　3次以上の方程式の解から作る体についても､この様な自己同型の群を作って分析します。

　4番目の例として､G={0,1,2,3}で､演算は”足して4で割った余り”とします。
　例えば､2※3=1ですね。乗積表を作れば､演算※で閉じてる事も結合法則も単位元=0も明らかです。更に､0の逆元は0､1の逆元は2､2の逆元は2､3の逆元は1である事も判る。
　しかし､これまで述べた4つ例の群は全て演算※に関し､交換法則(a※b=b※a)が成立します。この様に交換法則が成立する群を”可換群”と言いますが､大抵の群は交換法則が成立しないので､可換群とは非常に特別な例なんです。しかし､この可換群こそが解の公式と密な関係を持つんですね。
　因みに､可換群はアーベルの名をとりアーベル群とも呼びます。
　　

対称性と群の密な関係

　先述した様に､群は方程式の解の構造を分析する過程で生まれたが､今では代数学だけでなく､広範囲に重要な役割を果たします。それは(図形の)対称性と群とは表裏一体の関係にあるからです。
　まず2等辺三角形を例に取ると､左右対称とは裏返す事で自身に重なる事ですが。
　そこで自身に重なる(対称)操作を”続けて行う”という演算に対し､群で表現すれば､何もしない操作をeと裏返す操作をfとします。
　この時､eとfの乗積表を作れば､この僅か1つの対称操作の群も､例2と例3の群と同類である事は明らかですね。

　では､正三角形の対称操作はどんな群になるのか？
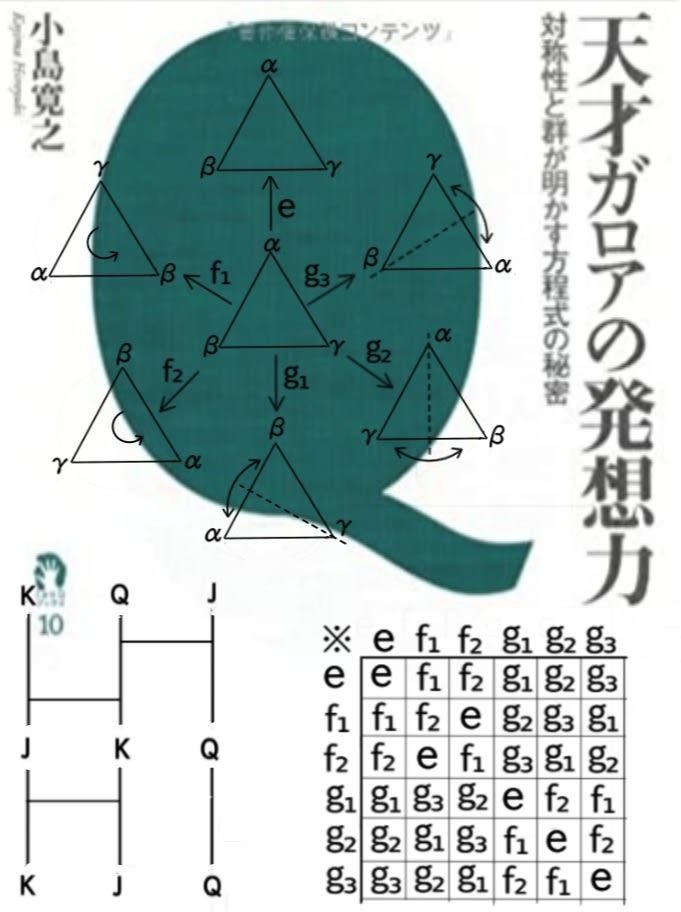
　正3角形には2等辺三角形と同じ(裏返す)線対称に加え､(回転しても変わらない)回転対称がある。線対称の軸は3本あるので､3つの対称操作(g₁,g₂,g₃)がある。また､回転の対称操作は120度と240度の2つ(f₁,f₂)があり､残るは”何もしない”対称操作eですね。
　そこでこれら6個の対称操作に対し､”繋げる”事を演算※と定義し､fの操作の後にgの操作を繋げる事をg※fとすれば､g₁※f₁=g₂です。

　例5として､この正3角型の対称操作の集合G={e,f₁,f₂,g₁,g₂,g₃}で､演算※={2つの対称操作を行い1つの対称操作に}とする。乗積表を作れば36個の演算結果が出ますが､交換法則が成立しないのは明らかですね(イラスト参照)。
　この様な群を”非可換群”と呼びますが､この群も3本のアミダくじの群と同類です。
　つまり､正3角形の頂点を反時計回りにα,β,γとすると､f₁:αβγ→γαβ､g₂:αβγ→αγβであるから､αβγをアミダのKQJに対応すれば､f₁はτにg₂はσに対応する。故に､正3角形の対称操作も6つ､アミダくじも6つですから､同類と言えるんですね。
　
　では､もっと複雑な正方形の対称操作はどんな群になるのか？
　正3角形と同様に､裏返しの対称操作は縦横の2つと斜めの2つの計4つ(S₁,S₂,S₃,S₄)ですね。回転の対称操作は反時計回りに90度､180度､270度の3つ(R₁,R₂,R₃)で､何もしない操作eを含め､合計で8つの対称操作があります。
　故に例6として､正方型の対称操作G={e,R₁,R₂,R₃,S₁,S₂,S₃,S₄}で､演算※={2つの対称操作を行い1つの対称操作に}とする。乗積表を作れば64個の演算結果が出ますが､これも交換法則が成立しないのは明らかですね。
　正方形の対称操作の特徴として､”2回の線対称操作は1回の回転対称操作”となり､これは”回転操作→裏返し操作＝裏返し操作”を意味します。
　それに､この群のもう1つの特徴は”どの元も4つ繋ぐと単位元になる”がある。これはアミダくじが”6つ繋ぐと元の素アミダに”戻るのと同じですね。

　以上で､群というものをアミダくじと図形の対称性を用いて､長々と説明しましたが。群の対称操作というのが後々に重要な要素となってきます。
　そういう私も｢方程式のガロア群｣(金重明著)で群を理解したつもりでしたが､まだまだ甘いみたいですね。
　勿論､群や体を完璧に理解してる人なら､この記事は不必要ですが､一応念の為に紹介しました。

　次回は､対称性の表現としての群と部分群に関して述べたいと思います。