昨日お知らせした「2時間でわかる・使える統計学セミナー」(12月4日:午後2時~4時、東京商工会議所・中野支部)のPRも兼ねて、統計学でもっとも重要な「かたち」である分布について、これから何回か使って、ちょっとゆるめに書かせていただきたいと思います。
さて、はじめは正規分布(せいきぶんぷ)についてです。
分布とは国語辞典によると、「分かれて広くあちこちにあること。また、あちこちに置くこと。」となっています。統計はデータを扱う手法ですから、要は「データがあちこちに散らばっている」状態と考えてください。
散らばり方にはさまざまな形があります。まんべんなく一様に散らばっている状態を、一様分布と言います(まんま、ですね)。でも、世の中をざっと見渡してみると、一様分布はあまり見かけません。
たとえば、人の身長です。
ある会社に従業員が1,000人いたとします。全従業員の背の高さを測ってみたら、一番低い人が141cm、一番高い人が190cm、平均165cmでした。
背の低い方から順に高い方へ、1cmきざみでグループを作ってもらったらどうなるでしょう。1cmきざみですから、グループを50作ることができます。
そのとき、50のグループそれぞれの人数がまんべんなく20人ずつだった(一様分布)・・・なんてことは、まずあり得ないでしょう。普通は、平均の165cmあたりが一番多くて、141cmや190cmの人はほとんどいないと思います。
また、近所の雑木林に行ってどんぐりを100個拾ってきて大きさを測っても似たような散らばり具合になるでしょう。
食堂でお味噌汁を100杯作ったときの1杯あたりの量もやはり同じように、極端な値は少なくて平均に近いところの数が多くなるはずです。
そうした「散らばり具合」には大体次のような特徴があるはずです。
(1)小さい方と大きい方の両極端に近いグループほどメンバーの数は少なくなっている。
(2)全体の平均あたりが一番数が多くなっている。
(3)その状態をグラフにすると山型または釣鐘(ベル)型になる。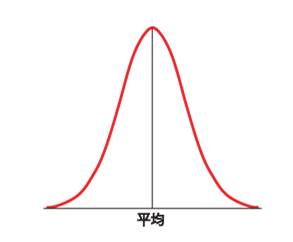
この分布のことを正規分布(normal distribution)と呼びます。ガウス分布、ベルカーブなどと言うこともあります。
正規分布は世の中のあちらこちらで見かけます。もちろん、様々な分布のかたちがありますから、森羅万象なんでも正規分布、とは言えませんけれど。
統計を使って何かを調べる時に、この正規分布を前提にすることがたくさんあります。
扱うデータがきれいに正規分布してなくても、「まあ、大体こんなもんだろう。それほどズレてはいないし。」ということで使われることが多いのです。
この分布のかたちは、社会現象にも自然現象にもよく現れます。
人材育成に関して言えば、社員の能力もこのかたちにばらついている(散らばっている)ことが多いと思います。(もしそうなっていなければ、何かが”不自然”なのかもしれません)
正規分布、是非覚えておいてください。
参考: http://www.albert2005.co.jp/technology/data/n_distribution.html
セミナー: http://event.tokyo-cci.or.jp/event_detail-51144.html
(人材育成社)










