分数の割り算

　先週末、ゴジ健さんが分数の割り算の仕組みについて渾身の論文を書かれたが、私も職業柄、自分なりの考えをまとめてみなければならないと思っていた。しかし、センター試験のため落ち着かぬ日々を過ごしたので、思うように時間がとれず今日まで延び延びになってしまった。ゴジ健さんよりも分りやすい説明ができる自信はないが、試してみる。
　
　分数の割り算を考える前に、分数の掛け算について確認しておいたほうが割り算の仕組みを考えるのに便利なので、まず掛け算について考えてみる。
　
　（3/5×3/4＝3×3/5×4 になる理由）
１辺が１の正方形の面積は 1×1＝1 。これをもとにして縦が3/5、横が3/4 の長方形の面積を考えると、下図（１）の斜線の部分の面積を考えることになる。
　　　　　　　　　　　　　　　　　　　　　（図１）　　　　　　　　　　　　　　　　（図２）
　
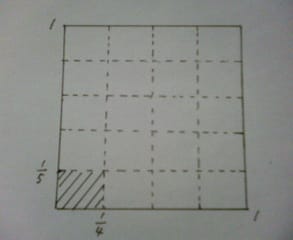
まず（図２）の斜線部の面積を求めると、縦は１を５つに分けた長さで 1/5、横は１を４つに分けた長さで 1/4 であるから、その面積を求める式は 1/5×1/4 となり、それは図から明らかなように正方形の面積１を縦に５つずつ、横に４つずつに分けたもの、すなわち 5×4＝20 個に分けたものであるから、面積は1/20 となる。したがって、1/5×1/4＝1/5×4＝1/20 である。
　そこで、これをもとにすると、（図１）の縦3/5、横3/4 の長方形の面積は、（図２）で求めた面積1/20 の図形が、縦３個、横３個、つまり 3×3＝9個集まったものである。つまり、面積が1/20 の図形が９個集まった長方形の面積は、9/20 となる。結局、これが縦3/5、横3/4 の長方形の面積であるから、
　　　3/5×3/4＝3×3/5×4＝9/20 　　　となる。

　これをもとにして分数の割り算に進む。

例えば、「4/5ha の畑をトラクターで耕すのに 3/4 時間かかった。このトラクターが１時間あたりに耕す面積を求めよ」という問題を考えてみる。
　ゴジ健さんが論破されたように、割り算とは『あるものに対しての１単位あたりの数を求める』ことである。「１単位当たり」というのを「もとにする量を１としたとき」と言い換えてもよい。すなわち、「比べる量は、もとにする量を１としたときにいくつになるのかを求めるのが割り算」と言いかえることができる。
　そう考えると、上の問題で、もとにするのは時間であり、時間を１時間としたときにどれだけの面積を耕すことができるのかを求めることになるから、式は、
　　4/5÷3/4　　となる。これを図にすると、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（図３）

斜線は 3/4 時間で耕した 4/5ha を表している。この図をもとにして、１時間で耕す量を考えてみると、下の（図４）の斜線部の大きさを求めることになる。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（図４）

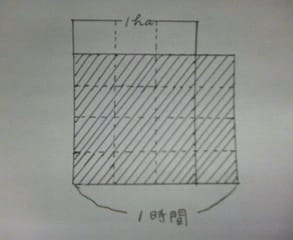
（図３）と（図４）を見比べてみれば、（図４）の斜線部の大きさを求めるには、4/5ha の 4/3 倍の大きさを求めればいいことが分る。すなわち、
　　　　4/5÷3/4＝4/5×4/3＝4×4/5×3 である。

これは比の考えを使うと、さらに分りやすい。3/4 時間と１時間では、時間の長さが３：４となる。これを図に表すと、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（図５）

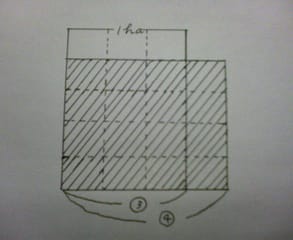
図から明らかなように、１時間で耕せる面積は、3/4 時間で耕せる面積の 4/3 倍となるのである。

　分数の割り算の仕方を、塾では「割る数の逆数（分母分子を入れ替えた分数）を掛けろ」と教える。この問題の場合は、トラクターで耕す時間の基準となる１時間は 3/4 時間の何倍であるかを、（図５）など利用して考えて、4/3 倍の時間であると分れば、１時間に耕せる面積は 3/4 時間で耕した 4/5ha を 3/4 の逆数 4/3 倍した面積、すなわち、4/5÷3/4＝4/5×4/3＝4×4/5×3＝16/15 haとなるのを理解することはできると思う。

　しかし、難しい。もっと簡単で明快に説明できればいいのだが、私ではこれが精一杯だ。