4元数の積は次のようになった。
(a+bi+cj+dk)(x+yi+zj+wk)
=(ax-by-cz-dw)
+(ay+bx+cw-dz)i
+(az+cx+dy -bw)j
+(aw+dx+bz-cy)k
ここで、d=0,w=0とおくと3元数の積が現れる。
また、c=0,d=0,z=0,w=0とおくと、2元数(複素数)の積が現れる。
2元数(複素数)の場合、
(a+bi)(x+yi)=(ax-by)+(ay+bx)iとなり、2元数の積は2元数になっていることがわかる。これに対して、3元数は
(a+bi+cj)(x+yi+zj)
=(ax-by-cz)+(ay+bx)i+(az+cx)j+(bz-cy)kとなり、3元数の積は3元数にならず、4元数になっていることがわかる。虚数単位kが消えないのである。
これは2元数と4元数では成り立っている2つの原則(体の原則と絶対値の原則)が、3元数では成り立っていないことを意味している。3元数(1,i,j)の積とみえるのは見かけだけで、実際は4元数(1,i,j,k)の積でd=0,w=0の特殊な(退化した)場合なのである(矢野忠『四元数の発見』参照)。3元数は合理的な数ではないのである。
3元数の積(a+bi+cj)(x+yi+zj)
=(ax-by-cz)+(ay+bx)i+(az+cx)j+bzij+cyji
は下線部で行き止まりだった。
ここに4元数が「縮退(degeneracy)」していた。ハミルトンは絶対値の原則に照らしij=-ji=kと想定することによって、この縮退(退化もdegeneracyである)を解いたのである。
ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づいた。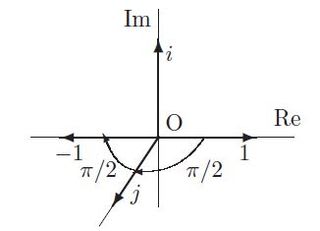
これが出発点だった。さらにハミルトンは3つの元1,i,jに垂直な第4の元kに気づいたのである。「2元数と3元数」で示した図にもどることにしよう。
(a+bi+cj+dk)(x+yi+zj+wk)
=(ax-by-cz-dw)
+(ay+bx+cw-dz)i
+(az+cx+dy -bw)j
+(aw+dx+bz-cy)k
ここで、d=0,w=0とおくと3元数の積が現れる。
また、c=0,d=0,z=0,w=0とおくと、2元数(複素数)の積が現れる。
2元数(複素数)の場合、
(a+bi)(x+yi)=(ax-by)+(ay+bx)iとなり、2元数の積は2元数になっていることがわかる。これに対して、3元数は
(a+bi+cj)(x+yi+zj)
=(ax-by-cz)+(ay+bx)i+(az+cx)j+(bz-cy)kとなり、3元数の積は3元数にならず、4元数になっていることがわかる。虚数単位kが消えないのである。
これは2元数と4元数では成り立っている2つの原則(体の原則と絶対値の原則)が、3元数では成り立っていないことを意味している。3元数(1,i,j)の積とみえるのは見かけだけで、実際は4元数(1,i,j,k)の積でd=0,w=0の特殊な(退化した)場合なのである(矢野忠『四元数の発見』参照)。3元数は合理的な数ではないのである。
3元数の積(a+bi+cj)(x+yi+zj)
=(ax-by-cz)+(ay+bx)i+(az+cx)j+bzij+cyji
は下線部で行き止まりだった。
ここに4元数が「縮退(degeneracy)」していた。ハミルトンは絶対値の原則に照らしij=-ji=kと想定することによって、この縮退(退化もdegeneracyである)を解いたのである。
ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づいた。

これが出発点だった。さらにハミルトンは3つの元1,i,jに垂直な第4の元kに気づいたのである。「2元数と3元数」で示した図にもどることにしよう。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます